一、高考热点分析

　　平抛物体的运动规律及其研究方法，是近几年来高考热点。这一知识点常与匀强电场中带电粒子作类似平抛运动联系在一起，综合考查学生的应用知识的能力。因此，现在必须对这一知识引起足够的重视。

二、高考回顾

1、如图所示，排球场总长为18m，设球网高度为2m，运动员：在离网3m的线上(图中虚线所示)正对网前跳起将球水平击出(空气阻力不计)。

　　（1）设击球点在3m线正上方高度为2.5m处，试问击球的速度在什么围内才能使球既不触网也不越界．

　　（2）若击球点在3m线正上方的高度小于某个值，那么无论水平击球的度多大，球不是触网就是越界，试求这个高度(g取10m／s2)．

解答：

　　（1）作出如下图所示的平面图，若刚好不触网，设球的速度为v1，在水平位移为3m的过程中，

　　　　　水平方向上有：s＝v0t，即3＝v1t　①

　　　　　竖直方向有：y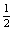＝gt2，即2.5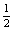—2＝gt2　②

　　　　　由①②两式得：v1＝3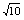m／s

　　　　　同理可得刚好不越界的速度v2＝12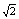m／s

　　　　　故范围为：3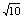m／s＜v＜12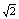m／s

　　（2）设发球高度为H时，发出的球刚好越过球网，落在边界线上

　　　　 则刚好不触网时有：s＝v0t，即3＝v0t　③

　　　　 H－h = 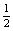gt2

　　　　 即H－2 =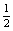gt2　　④

　　　　同理，当球落在界线上时有：12＝v0t′⑤

　　　　H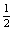＝ gt′2 　⑥

　　解③④⑤⑥得H＝2．13m ，即当击球高度小于2.13m时，无论球的水平速度多大，则球不是触网就是越界．

2、在离水平地面高度为H处有一小球A，在A的右方，与它的水平距离为S处的地面上，有另一小球B，如图所示。今同时把两球抛出，A沿水平向右，抛出时的初速度为vA，B竖直向上，抛出时的初速度为vB，设H、S是已知的，问：

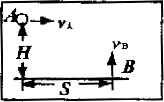
　　（1）要使两球在空中相遇，vA、vB应满足什么条件？

　　（2）若从抛出到相遇所经历时间最长，则B走的路程为多少？

　　（3）若B在上升过程中与A相遇，vB应满足什么条件？

解析：

　　（1）设A从抛出至它落地历时t1，有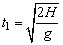，A的水平射程vAt1>S，才能在空中相遇，有。

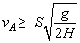　　　　相遇处B上升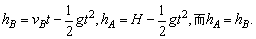

　　　　

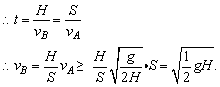
　　（2）显然当B上升至落地，在地上相遇，历时最长，

　　　　　.

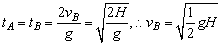　　　　　B上升最大高度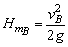，故B总的路程为。

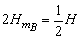　　（3）若B球上升阶段与A相遇，v=vB－gt2>0，vB>gt2.

　　　　　由于vBt2=H，∴

-END-