1、据美联社2002年10月7日报道，天文学家在太阳系的9大行星之外，又发现了一颗比地球小得多的新行星，而且还测得它绕太阳公转的周期约为288年. 若把它和地球绕太阳公转的轨道都看作圆，问它与太阳的距离约是地球与太阳距离的多少倍. （最后结果可用根式表示）
解析：
设太阳的质量为M；地球的质量为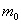
绕太阳公转的周期为T0，太阳的距离为R0，公转角速度为
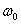；新行星的质量为
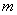，绕太阳公转的周期为T，与太阳的距离为R，公转角速度为
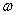，根据万有引力定律和牛顿定律，得
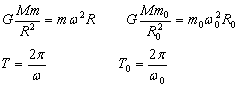
由以上各式得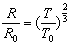
已知 T=288年，T0=1年得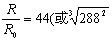
）
2、宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L.若抛出时的初速度增大到2倍，则抛出点与落地点之间的距离为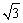
L.已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G，求该星球的质量M.（提示：设小球质量为m，该星球表面重力加速度为g，则
）
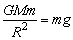解析：
设抛出点的高度为h，第一次平抛的水平射程为x，则有x2＋h2=L2.
由平抛运动规律知，当初速度增大到2倍，其水平射程也增大到2x，则：
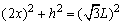
联立以上两式得：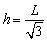
设该星球上的重力加速度为g，由平抛运动的规律，得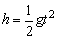 
由万有引力定律与牛顿第二定律有：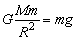
其中m为小球质量。
联立解得：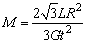
3、地球半径R=6400km，地面的重力加速度g=9.8m/s2.地核的体积约为整个地球体积的16%，地核的质量约为地球质量的34%.试估算地核的平均密度。
解析：
本题求的是地核的平均密度，而由于地核与地球的质量关系和体积关系均已知，故只要求出地球的密度，地核的密度便迎刃而解，如果把思路限定在地核上，则会有不知如何下手之感。
不计地球自转的影响，地球对物体的引力为物体的重力，即：
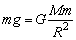
所以，地球的质量为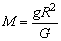
地球的平均密度为：
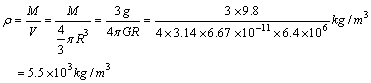
设地核的平均密度为ρ′，地核的质量和体积分别为M′和V′，则：
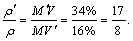
所以，地核的平均密度为：
