|
一、选择题(4分×10=40分)
1、一太空探测器进入了一个圆形轨道绕太阳运转,已知其轨道半径为地球绕太阳运转轨道半径的9倍,则太空探测器绕太阳运转的周期是( )
A.3年 B.9年
C.27年 D.81年
2、引力常量G已知,要想计算出地球的质量,仅已知下列哪组数据是可行的( )
A.月球绕地球运行的周期和月球到地球中心的距离
B.地球同步卫星离地面的高度
C.地球绕太阳运行的周期和地球到太阳中心的距离
D.某颗人造卫星绕地球运行的线速度和周期
3、两颗质量相等的人造卫星a、b,绕地心运行的圆周轨道半径是ra和rb,且ra=2rb,下面说法中正确的是( )
A.由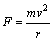 ,可知a受向心力是b的 ,可知a受向心力是b的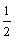 倍 倍
B.由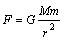 ,可知a受向心力是b的 ,可知a受向心力是b的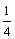 倍 倍
C.由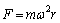 ,可知a受向心力是b的2倍 ,可知a受向心力是b的2倍
D.以上说法均不正确
4、设地面附近重力加速度为g,地球半径为R,人造地球卫星圆形轨道半径为r,那么以下说法正确的是( )
A.卫星在轨道上向心加速度大小为gR2/r2
B.卫星运行的线速度大小为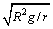
C.卫星运行的角速度大小为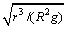
D.卫星运行的周期为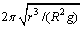
5、如图所示,A、B、C是地球大气层外圆形轨道上运行的三颗地球卫星,A、B质量相同,B、C质量不同,则( )
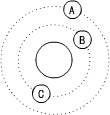
A.B、C速率相等,周期相等
B.A、B速率相等,周期相等
C.A的速率最大,周期最小
D.A的速率最小,周期最大
6、两颗人造地球卫星质量之比是1∶2,轨道半径之比是3∶1,下列说法中正确的是( )
A.周期之比是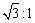
B.线速度之比是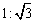
C.向心加速度之比是1∶9
D.向心力之比是1∶9
7、地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星离地面的高度为h,则地球同步卫星的线速度大小为( )
A.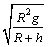 B. B.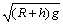
C.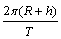 D. D.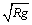
8、月球表面处的重力加速度是地球表面处的重力加速度的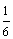 ,地球半径为月球半径的4倍,则登月舱靠近月球表面的环绕速度与人造卫星的第一宇宙速度之比是( ) ,地球半径为月球半径的4倍,则登月舱靠近月球表面的环绕速度与人造卫星的第一宇宙速度之比是( )
A.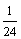 B. B.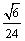
C.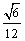 D. D.
9、一艘宇宙飞船绕一个不知名的行星表面以第一宇宙速度飞行,要测定该行星的平均密度,仅仅只需测定( )
A.运行周期 B.环绕半径
C.飞船线速度 D.行星周长
10、关于第一宇宙速度,下面说法中正确的是( )
A.它是人造地球卫星绕地球飞行的最小速度
B.它是近地圆形轨道上人造地球卫星的运行速度
C.它是能使卫星进入近地圆形轨道的最小发射速度
D.它是卫星在椭圆轨道上运行时在近地点的速度
[提示]
二、填空题(4分×4=16分)
11、在太阳系中,有九大行星绕着太阳运行,按照距太阳的距离排列,由近及远依次是:水星、金星、地球、火星、木星、土星、天王星、海王星和冥王星,如果把这些行星的运动近似为匀速圆周运动,那么它们绕太阳运动一周所用的时间最长的是________,运行角速度最大的是_______。
[答案]
12、“双星”就是在宇宙中有两颗质量分别为m1和m2的恒星,相距为d,且离其他星球很远。它们之间的距离保持不变,并都围绕两星连线上的一点,各自做匀速圆周运动,则其轨道半径之比R1∶R2=_____,线速度大小之比v1∶v2=_____。
[答案]
13、火星质量是地球质量的1/9,半径是地球半径的1/2,则一个宇航员在火星上的体重与在地球上体重之比为_______。
[答案]
14、假设地球的自转角速度加快,使赤道上的物体在随地球一起转动的同时,完全“漂浮”起来(处于完全失重状态),那么地球自转一周的时间T=_______(用R、g表示)=______分钟。(地球半径R=6.4×106m,结果取三位有效数字,g=10m/s2)。
[答案]
三、实验题(2分+6分=8分)
15、卡文迪许用巧妙的扭秤实验通过两次放大测出了引力常量G,这两次放大分别是指:
(1)__________ (2)__________
[答案]
16、一艘宇宙飞船飞近某一个新发现的行星,并进入靠近该行星表面的圆形轨道绕行数圈后,着陆在该行星上,宇宙飞船上备有以下实验仪器:
A.精确秒表一只 B.质量为m的物体一个
C.弹簧秤一个 D.天平一台(附加码)
已知宇航员在绕行及着陆后各作一次测量,依据测量的数据,可求出该星球的质量M,半径R(已知万有引力常量为G)
(1)两次测量所选用的仪器分别为_______、_______。(用该仪器的字母序号表示)
(2)两次测量的物理量分别为________、________。
(3)用该测量数据,求得该星球的质量M=_________ ,该星球的半径R=___________。
[答案] 四、综合题(8分+8分+10分+10分=36分)
17、太阳距银河系中心约2.5×104光年,太阳绕银河系中心的运动可以视为匀速圆周运动,运动周期约为1.7×108年,太阳光照射到地球上需经过500s,由以上数据估算银河系质量大约是太阳质量的多少倍?说明分析问题的依据,写出主要过程。(保留两位有效数字)
[解答]
18、在月球上以初速度v0竖直上抛一个小球,经过时间t落回到抛出点,已知月球的半径为R,引力常量为G,求:(1)月球的质量;(2)月球的平均密度。
[解答]
19、a、b两颗卫星,在同一轨道平面内绕地球做匀速圆周运动,运行方向相同。地球半径为R,卫星a距地面高度为R,卫星b距地面高度为3R,则a、b两卫星周期之比是多少?某时刻,两卫星正好通过地面上同一点的正上方,那么a卫星至少经过多少个周期,两卫星相距最远
[解答]
20、宇宙飞船以5m/s2的加速度匀加速竖直上升,在飞船中用弹簧秤测得质量为10kg的物体重为75N,若已知地球半径R为6400km,求测量时飞船所处的位置距地面的高度h。(地球表面上的重力加速度取g=10m/s2).
[解答]
21、某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,试问,春分那天(太阳光直射赤道)在日落12小时内有多长时间该观察者看不见此卫星?已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对光的折射。
[解答] - 返回 -
|