追及和相遇问题
在运动学中存在一个追及相遇问题,往往涉及追及、相遇或避免碰撞问题。这类问题是运动学中较为复杂且有一定实际意义的一类习题,问题中一般涉及两个物体的运动过程,而且每个物体的运动规律不一定相同,在解题时要综合运用运动学的规律。追及、相遇的条件是两物体同时到达某位置。避免相碰的条件是两物体同向运动在速度相等时能否追上,两物体相向运动在停下时是否存在一定的距离。
1、甲、乙两车同时同地同向出发,甲以v甲=16m/s初速度,a甲=2m/s2的加速度做匀减速运动,乙以初速度v乙=4m/s,加速度a乙=1m/s2做匀加速运动,求:
(1)两车相遇前二者间的最大距离;
(2)两车再次相遇所用时间.
解析:
开始时v甲>v乙,两者间距离增大,但甲减速,乙加速,当二者速度相等时距离最大。
此后甲车速度小于乙车速度,距离减小,位移相等时再相遇。
(1)设速度相同时,运动时间为t1。
相距最远的条件是v甲-a甲t1=v乙+a乙t1
解得t1=4s
则最远距离:

代入数值得:△s=24m.
(2)设再次相遇的时间为t2,
相遇条件为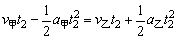 .
.
代入数值解得:t2=8s,t2′=0(舍去)。
2、一辆摩托车在平直公路上由静止开始做匀加速运动,能达到的最大速度为30m/s,要想用3分钟时间追上前面1000m远处以20m/s速度匀速前进的汽车,求摩托车的最小加速度?
解:3分钟内汽车的位移:
s1=vt=20×3×60=3600m
3分钟摩托车追上汽车时经过的位移:
s2=s+s1=1000+3600=4600m
摩托车的运动分为两个阶段,
在t1时间内做初速度为零,加速度为a的匀加速直线运动,
在(t-t1)的时间内以最大速度v2=30m/s做匀速运动,则:

又因为v2=at1,所以
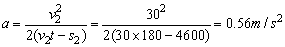 .
.