不等式是中学数学的基础和重要部分，它可以渗透到数学的其它内容中，在实际生活中有广泛的应用，是高考的重要内容。在复习不等式时应注意等价转化思想、分类讨论的思想、函数与方程的思想以及化归思想在不等式中的应用，掌握通性通法。提高应用意识，总结不等式的应用规律，才能提高解决问题的能力，在实际应用中，主要有构造不等式求解或构造函数求函数的最值等方法，求最值时要注意等号成立的条件，避免不必要的错误。
(一)知识网络结构
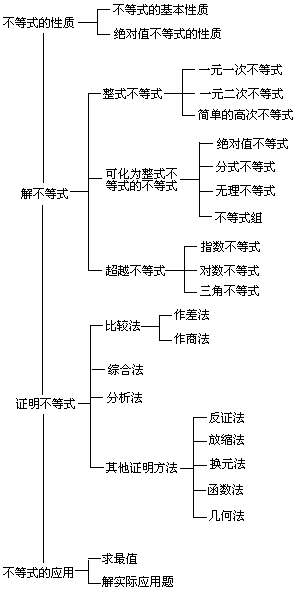
(二)不等式的性质
1、实数的运算性质和大小顺序之间的关系；
a－b>0
a>b；
a－b=0
a=b；
a－b<0
a<b.
2、不等式的基本性质
（1）对称性：a>b
b<a；
（2）传递性：a>b，b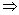>c
a>c；
（3）可加性：a>b，c∈R
a＋c>b＋c；
（4）可乘性：a>b，c>0
ac>bc；a>b，c<0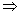
ac<bc.
3、不等式的运算性质
（1）加法：a>b，c>d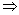
a＋c>b＋d；
（2）减法：a>b，c<d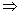
a－c>b－d；
（3）乘法：a>b>0，c>d>0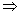
ac>bd；
（4）除法：a>b>0，0<c<d
；
（5）乘方：a>b>0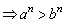
（n∈N*且n>1）
（6）开方：a>b>0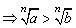
（n∈N*且n>1）
（7）倒数：a>b，ab>0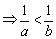
.
（三）不等式的证明方法与主要依据
1、证明不等式的方法：
证明不等式的常用方法有：比较法、综合法、分析法．此外，在证明不等式中，有时还要运用综合分析法、放缩法、换元法、反证法．
2、证明不等式的主要依据
（1）a－b>0
a>b；a－b<0
a<b.
（2）不等式的性质.
（3）重要不等式及定理：
①a2≥0（a∈R）；
②a2＋b2≥2ab（a∈R，b∈R）；
③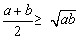
（a∈R＋，b∈R＋）；
④a3＋b3＋c3≥3abc（a，b，c∈R＋）；
⑤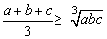
（a，b，c∈R＋）；
⑥|a|－|b|≤|a±b|≤|a|＋|b|；
⑦|a1＋a2＋…＋an|≤|a1|＋|a2|＋…＋|an|；
（注：搞清楚以上定理取“=”号的条件）
⑧|x|<a（a>0）
x2<a2
－a<x<a；
⑨|x|>a（a>0）
x2>a2
x<－a或x>a.
（四）不等式的解法
1、绝对值不等式、高次不等式的解法
1、不等式的性质、重要不等式、绝对值不等式是整章的基本内容，是证明不等式和解不等式的知识基础，应熟练掌握和运用．
例1、设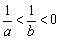
，则在①a2>b2；②a＋b>2
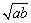；③ab<b2；④a2＋b2>|a|＋|b|这四个不等式中，恒成立的个数是（ ）
A．0 B．1 C．2 D．3
[分析与解答]
例2、已知正数x，y满足x+2y=1，求
的最小值．
[分析与解答]
2、不等式的证明
不等式证明方法较多，具体问题具体分析是证明不等式的精髓，灵活地选用证明方法是证明不等式的技巧．巧妙地变形是证明不等式的关键，联系和联想是证明不等式的重要观点，提高思维能力是证明不等式的落脚点．
例3、已知0<a<1，求证：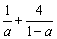
≥9.
[分析与解答]
3、不等式解法
不等式的解法是化归与转化思想的充分运用，将超越不等式转化为代数不等式、无理不等式转化为有理不等式、高次或分式不等式转化为一元一次、二次不等式等，应注意转化过程的等价性．
例4、解不等式：
[分析与解答]
例5、解关于x的不等式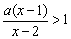
（a∈R）.
[分析与解答]
4、不等式的应用问题
例6、（全国高考试题）建造一个容积为8m3，深为2m的长方体无盖水池，如果池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为______元.
[分析与解答]
例7、（全国高考试题）甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为b；固定部分为a元．
（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域；
（2）为了使全程运输成本最小，汽车应以多大的速度行驶？
[分析与解答]
