|
一、一周知识概述
本周我们学习电流表的工作原理和磁场对运动电荷的作用两节内容。电流表的工作原理实质上是安培力的一个具体的应用,学习时要注意线框各边受安培力的方向,画出简明的受力图。
运动电荷在磁场中所受洛伦兹力的大小与哪些因素有关系,及其方向的判断是这一节的重点。洛伦兹力对运动电荷不做功是它的一个重要特点,学习时要正确理解。
二、重、难点知识归纳与讲解
1、电流表的工作原理
(1)匀强磁场中的安培力矩
如图a所示,矩形线圈abcd放在匀强磁场中,线圈平面与磁场平面平行,线圈可以线O′O转动。设磁场的磁感应强度为B,线圈的面积为S,电流大小为I,则ab边和cd所受的安培力大小Fab=Fcd=BILab,由图b可知磁场对通电线圈的磁力矩为 。 。

对于线圈平面与磁场方向的夹角为θ,线圈的匝数为N的通电线圈,安培力矩M=NBIScosθ.
(2)安培力矩公式的适用条件
①匀强磁场,且转轴(OO′)与B垂直(对于平行于B的任意转轴,安培力矩为零)。
②任意形状的平面线圈都适用。
(3)电流表工作原理
电流表中有均匀辐向磁场所以线圈转动后,受安培力力矩不变M1=NBIS。弹簧由于线圈的转动而产生一个反向的力矩M2=kθ。由线圈静止得M1=M2,即 。 。
2、磁场对运动电荷的作用
(1)洛伦兹力是磁场对运动电荷的作用,它是安培力的微观本质。安培力是洛伦兹力的宏观表现。
(2)洛伦兹力的大小
①当电荷速度方向垂直于磁场的方向时,磁场对运动电荷的作用力,等于电荷量、速率、磁感应强度三者的乘积,即F=qvB.
②当电荷速度方向平行磁场方向时,洛伦兹力F=0。
③当电荷速度方向与磁场方向成θ角时,可以把速度分解为平行磁场方向和垂直磁场方向来处理,此时受洛伦兹力F=qvBsinθ。
(3)洛伦兹力的方向
安培力的方向可以用左手定则来判断,洛伦兹力的方向也可用左手定则来判断:伸开左手,使大拇指跟其余四个手指垂直,且处于同一平面内,把手放入磁场,让磁感线穿过手心,对于正电荷,四指指向电荷的运动方向,对于负电荷,四指的指向与电荷的运动方向相反,大拇指所指的方向就是洛伦兹力的方向。由此可见洛伦兹力方向总是垂直速度方向和磁场方向,即垂直速度方向和磁场方向决定的平面。
(4)洛伦兹力的特点
因为洛伦兹力始终与电荷的运动方向垂直,所以洛伦兹力对运动电荷不做功。它只改变运动电荷速度的方向,而不改变速度的大小。
三、重、难点知识剖析
1、洛伦兹力与电场力的比较
(1)与带电粒子运动状态的关系
带电粒子在电场中所受到的电场力的大小和方向,与其运动状态无关。但洛伦兹力的大小和方向,则与带电粒子本身运动的速度紧密相关。
(2)决定大小的有关因素
电荷在电场中所受到的电场力F=qE,与两个因素有关:本身电量的多少和电场的强弱。运动电荷在磁场中所受的磁场力,与四个因素有关;本身电量的多少、运动速度v的大小、速度v的方向与磁感应强度B方向间的关系、磁场的磁感应强度B。
(3)方向的区别
电荷所受电场力的方向,一定与电场方向在同一条直线上(正电荷同向,负电荷反向),但洛伦兹力的方向则与磁感应强度的方向垂直。
2、解决在洛伦兹力等多力作用下电荷运动问题的注意问题:
(1)正确分析受力情况是解决电荷运动问题的关键。要在详细分析问题给出的物理过程的基础上,认清洛伦兹力是怎么变化的。伴随着洛伦兹力的变化,物体的受力情况又发生了什么样的变化。
(2)受力变化演变,出现了什么新运动情况,电荷从什么运动状态过渡到什么运动状态。
(3)寻找关键状态各物理量之间的数量关系,选择合适的物理规律去求解,这些常常就是解题的关键之所在。
四、例题分析
例1、如图所示,一位于xy面内的矩形通电线圈只能绕Ox轴转动,线圈的四个边分别与x、y轴平行。线圈中电流方向如图。当空间加上如下所述的哪种磁场时,线圈会转动起来()
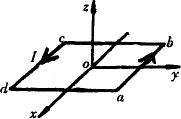
A.方向沿z轴的恒定磁场
B.方向沿z轴的变化磁场
C.方向沿y轴的恒定磁场
D.方向沿x轴的恒定磁场
解析:
根据题意,与Ox轴平行的两边受磁场力,才可能使线圈转动,而且这两边受的安培力方向不能与Oy轴平行。根据左手定则可以判断选项C是正确的。
答案:C
例2、如图所示,一只阴极射线管,左侧不断有电子射出,若在管的正下方放一通电直导线AB时,发现射线的径迹向下偏,则( )

A.导线中的电流从A流向B
B.导线中的电流从B流向A
C.若要使电子束的径迹向上偏,可以通过改变AB中的电流方向来实现
D.电子束的径迹与AB中的电流方向无关
解析:
由于AB中通有电流,在阴极射线管中产生磁场,电子受到洛伦兹力的作用而发生偏转,由左手定则可知,阴极射线管中的磁场方向垂直纸面向内,所以根据安培定则,AB中的电流方向应为从B流向A。当AB中的电流方向变为从A流向B,则AB上方的磁场方向变为垂直纸面向外,电子所受的洛伦兹力变为向上,电子束的径迹变为向上偏转。所以本题的正确选项应为B、C。
答案:BC
例3、如甲图所示,OA是一光滑、绝缘斜面,倾角为θ,一质量为m的带电体从斜面上的A点由静止开始下滑,如果物体的带电量为+q,整个装置处于垂直纸面向里的磁感应强度的大小为B的匀强磁场中,试求当物体离开斜面时,物体运动的速率及其沿斜面下滑的距离?(斜面足够长)
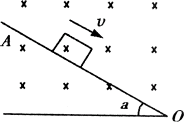
解析:
物体刚离开斜面时,对斜面的压力为零,物体受到斜面的支持力为零,受力分析如图乙,f=G2,以此可求速度v,下滑时由于洛仑兹力不做功,势能转化为动能,物体下降的高度h可以求出,物体下滑的距离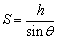 。 。
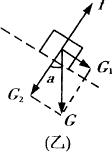
物体刚离开斜面时,f=Gcosθ,即qvB=mgcosθ,
所以得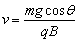 ,由于洛仑兹力不做功,mgh= ,由于洛仑兹力不做功,mgh=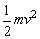 ①, ①,
沿斜面下滑的距离 ②,联立①②代入v得 ②,联立①②代入v得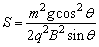 。 。
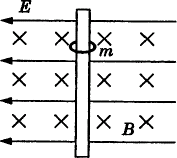
例4、如图所示,在竖直放置的绝缘直棒上套一个小环,其质量为0.1g,环带有电量为q=4×10-4C的正电荷,环与棒之间的动摩擦因数为μ=0.2,棒所在的空间分布有正交的匀强电场和匀强磁场,电场的场强为E=10V/m,磁场的磁感应强度为B=0.5T,现让环从静止开始下滑,求:
(1)环在下滑过程中的最大加速度;
(2)环在下滑过程中的最大速度。
解析:
要求出环在下滑过程中的最大加速度和最大速度,必须要了解环在整个下滑过程中的运动情况和受力情况。首先应对环进行受力分析,环在下滑过程中受到竖直向下的重力、水平向左的电场力、水平向右的洛伦兹力、水平方向的弹力和竖直向上的摩擦力。当环刚开始下滑时,环的速度很小,洛伦兹力也很小,环所受的电场力大于洛伦兹力。所以弹力的方向水平向右,环向下做加速运动,随着环的速度增大,环所受的洛伦兹力也增大,环所受的弹力变小,滑动摩擦力也变小,环在竖直方向所受的合力增大,环做加速度变大的加速运动,当环所受的洛伦兹力等于电场力时,弹力为零,滑动摩擦力也为零,此时,环在竖直方向的合力达到最大,加速度达到最大,为重力加速度g。随着环速度的进一步增大,环所受的洛伦兹力将大于电场力,弹力的方向变为水平向左,并随着洛伦兹力的增大而增大,环所受的滑动摩擦力增大,环在竖直方向所受的合外力变小,环做加速度变小的加速运动,当环所受的滑动摩擦力等于环的重力时,环的加速度为零,速度达到最大,接下去环将做匀速直线运动。
开始下滑时,环的受力如图(1)所示,当弹力为零时,物体在竖直方向只受重力作用,此时环的加速度最大,由牛顿第二定律可得:mg=mamax,
∴ amax=g=10m/s2.
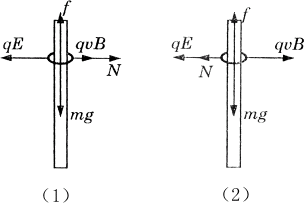
当环的加速度达到最大后,环受力情况如图(2)所示,当环的速度达到最大时,环所受的滑动摩擦力等于的重力,即f=mg。
而由于f=μN,N=qvmaxB-qE
∴ 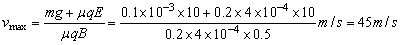 . .
- 返回 -
|