不等式这部分知识,渗透在中学数学各个分支中,有着十分广泛的应用.因此不等式应用问题体现了一定的综合性、灵活多样性,对数学各部分知识融会贯通,起到了很好的促进作用.在解决问题时,要依据题设与结论的结构特点、内在联系、选择适当的解决方案,最终归结为不等式的求解或证明.不等式的应用范围十分广泛,它始终贯串在整个中学数学之中.诸如集合问题,方程(组)的解的讨论,函数单调性的研究,函数定义域的确定,三角、数列、复数、立体几何、解析几何中的最大值、最小值问题,无一不与不等式有着密切的联系,许多问题,最终都可归结为不等式的求解或证明.
解不等式的核心问题是不等式的同解变形,整式不等式(主要是一次、二次不等式)的解法是解不等式的基础,利用不等式的性质及函数的单调性,将分式不等式、绝对值不等式等化归为整式不等式(组)是解不等式的基本思想,分类、换元、数形结合是解不等式的常用方法.方程的根、函数的性质和图象都与不等式的解密切相关,要善于把它们有机地联系起来,相互转化和相互变用.在解不等式中,换元法和图解法是常用的技巧之一.通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数、数形结合,则可将不等式的解化归为直观、形象的图形关系,对含有参数的不等式,运用图解法可以使得分类标准明晰.
比较法是不等式证明中最基本、也是最常用的方法,比较法的一般步骤是:作差(商)→变形→判断符号(值).
证明不等式的方法灵活多样,内容丰富、技巧性较强,这对发展分析综合能力、正逆思维等,将会起到很好的促进作用.在证明不等式前,要依据题设和待证不等式的结构特点、内在联系,选择适当的证明方法.通过等式或不等式的运算,将待证的不等式化为明显的、熟知的不等式,从而使原不等式得到证明;反之亦可从明显的、熟知的不等式入手,经过一系列的运算而导出待证的不等式,前者是“执果索因”,后者是“由因导果”,为沟通联系的途径,证明时往往联合使用分析法,两面夹击,相辅相成,达到欲证的目的.
虽然不等式的证明方法灵活多样,但比较法、综合法、分析法和数学归纳法仍是证明不等式的最基本方法.要依据题设、题断的结构特点、内在联系,选择适当的证明方法,要熟悉各种证法中的推理思维,并掌握相应的步骤,技巧和语言特点.
不等式应用问题体现了一定的综合性.这类问题大致可以分为两类:一类是建立不等式、解不等式;另一类是建立函数式求最大值或最小值.利用平均值不等式求函数的最值时,要特别注意“正数、定值和相等”三个条件缺一不可,有时需要适当拼凑,使之符合这三个条件.利用不等式解应用题的基本步骤:1°审题,2°建立不等式模型,3°解数学问题,4°作答.
题型一:不等式的性质
不等式的性质是证明不等式与解不等式的理论依据,因而是高考命题的重点考查的对象,若单独命题,主要是以选择题或填空题的形式出现,一般考查命题的真假的判断、大小比较、充要条件以及开放探索性问题等.
例1、(07上海卷)设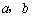 是非零实数,若
是非零实数,若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.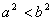 B.
B.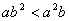
C. D.
D.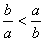
解:若a<b<0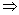 a2>b2,A不成立;若
a2>b2,A不成立;若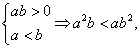 B不成立;
B不成立;
若a=1,b=2,则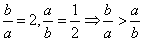 ,所以D不成立,故选C.
,所以D不成立,故选C.
例2、比较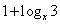 与
与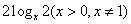 的大小.
的大小.
解:
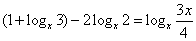 .
.
当 时,有
时,有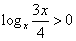 ,
,
此时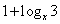
 .
.
当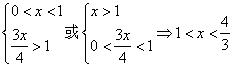 时,有
时,有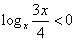 ,
,
此时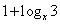
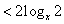 ;
;
当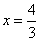 时,
时,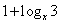
 .
.
题型二:解含参的不等式
例3、解关于x的不等式: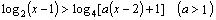 .
.
解:
原不等式等价于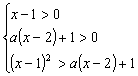 ①,即
①,即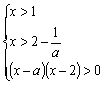 .
.
由于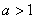 ,所以
,所以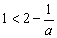 ,所以,上述不等式等价于
,所以,上述不等式等价于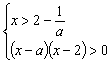 ②
②
(1)当 时,不等式组②等价于
时,不等式组②等价于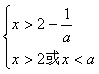
此时,由于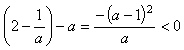 ,所以
,所以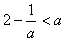 .
.
从而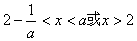 .
.
(2)当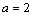 时,不等式组②等价于
时,不等式组②等价于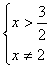
所以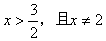 .
.
(3)当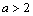 时,不等式组②等价于
时,不等式组②等价于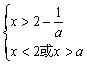
此时,由于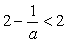 ,所以,
,所以,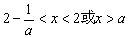 .
.
综上可知:
当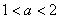 时,原不等式的解集为
时,原不等式的解集为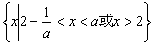 ;
;
当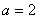 时,原不等式的解集为
时,原不等式的解集为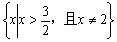 ;
;
当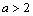 时,原不等式的解集为
时,原不等式的解集为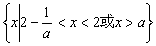 .
.
题型三:利用均值不等式求最值
例4、(1)已知a,b为正常数,x,y为正实数,且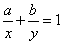 ,求x+y的最小值.
,求x+y的最小值.
(2)若a>b>0,求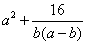 的最小值
的最小值
(3)求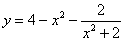 的最大值
的最大值
解:
(1)法一:直接利用基本不等式:
 ≥
≥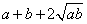 当且仅当
当且仅当 ,即
,即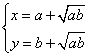 时等号成立.
时等号成立.
说明:为了利用均值不等式,本题利用了“1”的逆代换.
法二:消元化为一元函数:
由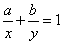 得
得 .
.

∵ x>0,y>0,a>0,∴ 由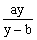 >0得y-b>0.
>0得y-b>0.
∴ x+y≥ .
.
当且仅当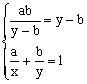 ,即
,即 时,等号成立.
时,等号成立.
法三:三角代换.令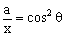 ,
,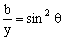 ,
, ∈(0,
∈(0,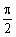 ).
).
∴ 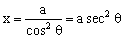 ,
,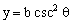 .
.
∴ x+y=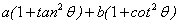
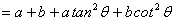 ≥
≥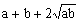 .
.
当且仅当 时,等号成立.
时,等号成立.
(2)分析: 的分母(a—b)b,而(a—b)+b=a,故问题突破口已显然! 也可以逐步进行:先对b求最小值
的分母(a—b)b,而(a—b)+b=a,故问题突破口已显然! 也可以逐步进行:先对b求最小值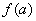 ,然后在对a求最小值.
,然后在对a求最小值.
解法一: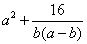 =[(a-b)+b]2+
=[(a-b)+b]2+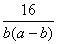
≥[2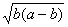 ]2+
]2+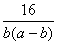 =4(a-b)b+
=4(a-b)b+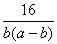 ≥16.
≥16.
当且仅当b=(a-b)且(a-b)b=2,即a=2b=2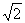 时取等号,故
时取等号,故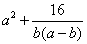 的最小值为16.
的最小值为16.
解法二:
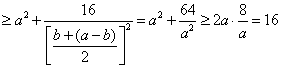 .
.
当且仅当b=(a-b)且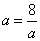 ,
,
即a=2b=2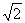 时取等号,故
时取等号,故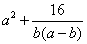 的最小值为16.
的最小值为16.
(3)
(若由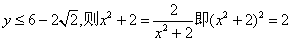 无解“=”不成立)
无解“=”不成立)
令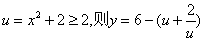 ,可以证明y(u)在
,可以证明y(u)在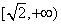 递减.
递减.
∴u=2,即x=0时,ymax=3.
点评:
用均值不等式求最值的前提条件是:“一正、二定、三相等”,这三个条件缺一不可,如果没有满足前提,要应根据题目创设情境,还要注意选择恰当的公式;一般来说“和定积最大,积定和最小”.由于均值不等式具有放缩功能,如果有多处用到,请注意每处等号的条件是否一致,若一致,则可取到最值,否则就不能取到最值.
题型四:不等式的证明
例5、已知a>0,b>0,且a+b=1.求证:(a+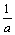 )(b+
)(b+ )≥
)≥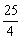 .
.
证法一:(分析法)
欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,即证4(ab)2-33(ab)+8≥0,
即证ab≤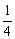 或ab≥8.
或ab≥8.
∵a>0,b>0,a+b=1,∴ab≥8不可能成立.
∵1=a+b≥2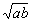 ,∴ab≤
,∴ab≤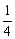 ,从而得证.
,从而得证.
证法二:(均值代换法)
设a=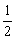 +t1,b=
+t1,b=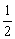 +t2.
+t2.
∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<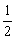 ,|t2|<
,|t2|< .
.

显然当且仅当t1=t2=0,即a=b=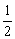 时,等号成立.
时,等号成立.
证法三:(比较法)
∵a+b=1,a>0,b>0,∴a+b≥2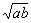 ,∴ab≤
,∴ab≤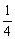 .
.
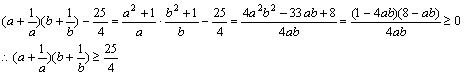
证法四:(综合法)
∵a+b=1, a>0,b>0,∴a+b≥2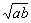 ,∴ab≤
,∴ab≤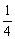 .
.
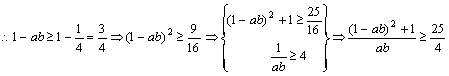 .
.
 .
.
例6、已知函数f(x)(x∈R)满足下列条件:对任意的实数x1,x2都有λ(x1-x2)2≤(x1-x2)[f (x1)-f(x2)]和|f (x1)-f(x2)|≤|x1-x2|,其中λ是大于0的常数.设实数a0,a,b满足f(a0)=0和b=a-λf(a).
(1)证明λ≤1,并且不存在b0≠a0,使得f(b0)=0;
(2)证明(b-a0)2≤(1-λ2) (a-a0)2;
(3)证明[f(b)]2≤(1-λ2) [f(a)]2.
解:
(1)任取x1,x2∈R,x1≠x2,则由λ(x1-x2)2≤(x1-x2)[f (x1)-f(x2)] ①,和|f(x1)-f(x2)|≤|x1-x2| ②,可知λ(x1-x2)2≤(x1-x2)[f(x1)-f(x2)]≤|x1-x2|·|f(x1)-f(x2)|≤|x1-x2|2,从而λ≤1.假设有b0≠a0,使得f(b0)=0,则由①式知0<λ(a0-b0)2≤(a0-b0)[f(a0)-f(b0)]=0,矛盾,∴不存在b0≠a0,使得f(b0)=0.
(2)由b=a-λf(a) ③,可知(b-a0)2=[a-a0-λf(a)]2=(a-a0)2-2λ(a-a0)f(a)+λ2[f(a)]2 ④,由f(a0)=0和①式,得(a-a0)f(a)=(a-a0)[f(a)-f(a0)]≥λ(a-a0)2 ⑤,由f(a0)=0和②式知,[f(a)]2 =[f(a)-f(a0)]2≤(a-a0)2 ⑥,则将⑤、⑥代入④式,得(b-a0)2≤(a-a0)2-2λ2(a-a0)2+λ2(a-a0)2=(1-λ2)(a-a0)2.
(3)由③式,可知[f(b)]2=[f(b)-f(a)+f(a)]2=[f(b)-f(a)]2+2f(a)[f(b)-f(a)]+[f(a)]2≤(b-a)2-2·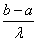 [f(b)-f(a)]+[f(a)]2=λ2[f(a)]2-
[f(b)-f(a)]+[f(a)]2=λ2[f(a)]2- (b-a) [f(b)-f(a)]+[f(a)]2≤λ2[f(a)]2-
(b-a) [f(b)-f(a)]+[f(a)]2≤λ2[f(a)]2-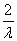 ·λ·(b-a)2+[f(a)]2=λ2[f(a)]2-2λ2[f(a)]2+[f(a)]2=(1-λ2)[f(a)]2.
·λ·(b-a)2+[f(a)]2=λ2[f(a)]2-2λ2[f(a)]2+[f(a)]2=(1-λ2)[f(a)]2.
题型五:不等式与函数综合
例7、已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m、n∈[-1,1],m+n≠0时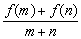 >0.
>0.
(1)用定义证明f(x)在[-1,1]上是增函数;
(2)解不等式:f(x+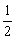 )<f(
)<f(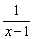 );
);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
思路分析:
(1)问单调性的证明,利用奇偶性灵活变通使用已知条件不等式是关键,(3)问利用单调性把f(x)转化成“1”是点睛之笔.
(1)证明:任取x1<x2,且x1,x2∈[-1,1],
则f(x1)-f(x2)=f(x1)+f(-x2)= ·(x1-x2).
·(x1-x2).
∵-1≤x1<x2≤1,
∴x1+(-x2)≠0,由已知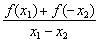 >0,又 x1-x2<0,
>0,又 x1-x2<0,
∴f(x1)-f(x2)<0,即f(x)在[-1,1]上为增函数.
(2)解:∵f(x)在[-1,1]上为增函数,
∴ 解得:{x|-
解得:{x|-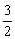 ≤x<-1,x∈R}.
≤x<-1,x∈R}.
(3)解:由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,
故对x∈[-1,1],恒有f(x)≤1,
所以要使f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,即要t2-2at+1≥1成立,
故t2-2at≥0,记g(a)=t2-2at,对a∈[-1,1],有g(a)≥0,
只需g(a)在[-1,1]上的最小值大于等于0,g(-1)≥0,g(1)≥0,
解得,t≤-2或t=0或t≥2.
∴t的取值范围是:{t|t≤-2或t=0或t≥2}.
点评:
本题是一道函数与不等式相结合的题目,考查学生的分析能力与化归能力.它主要涉及函数的单调性与奇偶性,而单调性贯穿始终,把所求问题分解转化,是函数中的热点问题;问题(2)、(3)要求的都是变量的取值范围,不等式的思想起到了关键作用.
题型六:不等式与数列综合
例8、设函数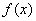 的定义域、值域均为R,
的定义域、值域均为R,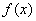 的反函数为
的反函数为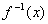 ,且对任意实数x,均有
,且对任意实数x,均有 .定义数列
.定义数列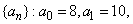
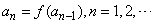 .
.
(1)求证: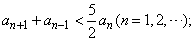
(2)设
(3)是否存在常数A和B,同时满足
①当n=0及n=1时,有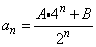 成立;
成立;
②当n=2,3,…时,有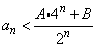 成立.
成立.
如果存在满足上述条件的实数A,B,求出A,B的值;如果不存在,证明你的结论.
(1)证明: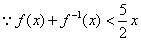 ,令
,令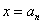 ,
,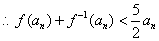 ,
,
即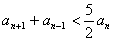 .
.
(2)证明: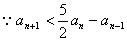 ,
,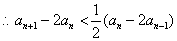 ,
,
 .
.
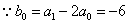 ,
,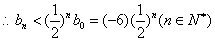 .
.
(3)解:由(2)可知: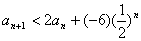 .
.
假设存在常数A和B,使得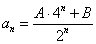 对
对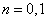 成立,则
成立,则
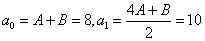 ,解得A=B=4.
,解得A=B=4.
由(2)可知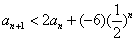 ,∴
,∴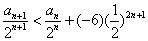 ,
,
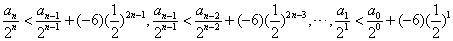 .
.
累加可得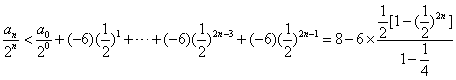
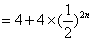 ,
,
∴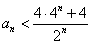 .
.
∴A=B=4满足题设.
题型七:不等式的实际应用
例9、设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ(λ<1),画面的上下各留8cm的空白,左右各留5cm的空白,问怎样确定画面的高与宽的尺寸,能使宣传画所用纸张面积最小?如果 ,那么
,那么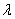 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
解:
设画面的高为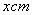 ,宽为
,宽为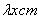 ,则
,则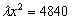 ,设纸张面积为
,设纸张面积为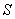 ,则有
,则有
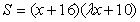
 ,
,
当且仅当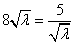 时,即
时,即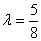 时,
时, 取最小值,此时,高
取最小值,此时,高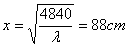 ,
,
宽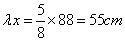 .
.
如果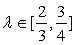 ,则上述等号不能成立.现证函数
,则上述等号不能成立.现证函数
S(λ)在 上单调递增.设
上单调递增.设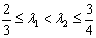 ,
,
则
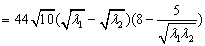 .
.
因为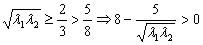 ,
,
又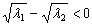 ,
,
所以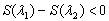 ,故
,故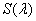 在
在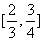 上单调递增,因此对
上单调递增,因此对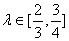 ,当
,当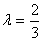 时,
时,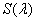 取得最小值.
取得最小值.