分类讨论思想是解决问题的一种逻辑方法,也是一种数学思想,这种思想在简化研究对象,发展思维方面起着重要作用,因此,有关分类讨论的思想的数学命题在高考试题中占有重要地位.
所谓分类讨论,就是在研究和解决数学问题时,当问题所给对象不能进行统一研究,我们就需要根据数学对象的本质属性的相同点和不同点,将对象区分为不同种类,然后逐类进行研究和解决,最后综合各类结果得到整个问题的解决,这一思想方法,我们称之为“分类讨论的思想”.
1. 分类讨论的思想方法是中学数学的基本方法之一,是历年高考的重点
⑴分类讨论的思想具有明显的逻辑特点;
⑵分类讨论问题一般涵盖知识点较多,有利于对学生知识面的考察;
⑶解决分类讨论问题,需要学生具有一定的分析能力和分类技巧;
⑷分类讨论的思想与生产实践和高等数学都紧密相关.
2. 分类讨论的思想的本质
分类讨论思想的本质上是“化整为零,积零为整”,从而增加了题设条件的解题策略.
3. 运用分类讨论的思想解题的基本步骤
⑴确定讨论对象和确定研究的区域;
⑵对所讨论的问题进行合理的分类(分类时需要做到不重复、不遗漏、标准统一、分层不越级);
⑶逐类讨论:即对各类问题详细讨论,逐步解决;
⑷归纳总结,整合得出结论.
4. 明确分类讨论的思想的原因,有利于掌握分类讨论的思想方法解决问题,其主要原因有:
⑴由数学概念引起的分类讨论:如绝对值定义、等比数列的前n项和公式等等;
⑵由数学运算要求引起的分类讨论:如偶次方根非负、对数中的底数和真数的要求、不等式两边同乘以实数对不等号方向的影响等等;
⑶由函数的性质、定理、公式的限制引起的分类讨论;
⑷由几何图形中点、线、面的相对位置不确定引起的分类讨论;
⑸由参数的变化引起的分类讨论:某些含参数的问题,由于参数的取值不同会导致所得结果不同,或由于不同的参数值要运用不同的求解或证明方法;
⑹其他根据实际问题具体分析进行分类讨论,如排列、组合问题,实际应用题等.
5. 分类讨论思想的类型
⑴问题中的变量或含有需讨论的参数的,要进行分类讨论的;
⑵问题中的条件是分类给出的;
⑶解题过程不能统一叙述,必须分类讨论的;
⑷涉及几何问题时,由几何元素的形状、位置的变化需要分类讨论的.
例1、(2007·上海)直角坐标系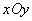 中,
中,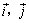 分别是与
分别是与 轴正方向同向的单位向量.在直角三角形ABC中,若
轴正方向同向的单位向量.在直角三角形ABC中,若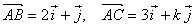 ,则k的可能值个数是( )
,则k的可能值个数是( )
A.1 B.2 C.3 D.4
解析:
由 (2,1),
(2,1),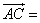 (3,k),得
(3,k),得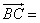 (1,k-1),
(1,k-1),
由于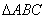 为直角三角形,则
为直角三角形,则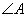 ,
,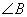 ,
, 都可能为直角,
都可能为直角,
由向量数量积为0,分别有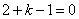 或
或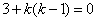 或
或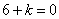 ,
,
解得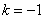 或
或 .
.
答案:B
点评:
本题主要考查向量运算及向量垂直的判定,也考查了学生分类讨论思想能力,引起分类的原因是直角三角形直角的不确定,但有的学生也可能想到位置有三种情况,故主观认为有三个值,这也是值得思考的.
例2、将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
A. B.
B. C.
C. D.
D.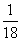
解析:
连续掷三次骰子出现点数的方法总数为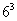 种,其中公差为0的等差数列有6个,公差为1或-1的等差数列有
种,其中公差为0的等差数列有6个,公差为1或-1的等差数列有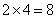 个,公差为2或-2的等差数列有
个,公差为2或-2的等差数列有 个,所以满足条件中的概率为
个,所以满足条件中的概率为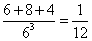 .
.
答案:B
点评:
本题主要考查概率基础知识,排列组合知识和等差数列的性质,由于取出的三个数成等差数列,则三个数由于顺序且公差不确定,所以需要分类进行计数.
例3、(2007·陕西)已知椭圆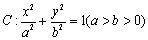 的离心率为
的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为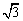 .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点,坐标原点O到直线l的距离为 ,求
,求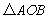 面积的最大值.
面积的最大值.
分析:
圆锥曲线方程的确定要了解其中参数字母具有的几何意义,掌握字母间的基本关系.
解:
(1)设椭圆的半焦距为c,依题意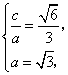
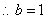 ,∴所求椭圆方程为
,∴所求椭圆方程为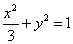 .
.
(2)设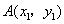 ,
,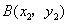 .
.
①当 轴时,
轴时, .
.
②当AB与x轴不垂直时,设直线AB的方程为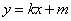 .
.
由已知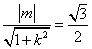 ,得
,得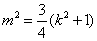 .
.
把 代入椭圆方程,整理得
代入椭圆方程,整理得 ,
,
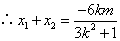 ,
,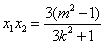 .
.
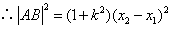


 .
.
当且仅当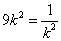 ,即
,即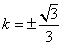 时等号成立.当
时等号成立.当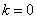 时,
时,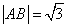 ,综上所述
,综上所述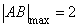 .
.
∴当|AB|最大时,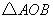 面积取最大值
面积取最大值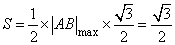 .
.
点评:
本题考查圆锥曲线的方程和直线与圆锥曲线间的位置关系.对于直线方程,根据斜率存在与否是本题产生讨论的原因.
例4、(2007·海南、宁夏)设函数 .
.
(1)若当x=-1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(2)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于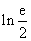 .
.
分析:
函数的极值、单调性是函数的重要性质.极值问题的解决,需要利用导数知识判断在该点两侧函数的单调性;而函数单调性的讨论则需要考察相应导数的符号问题.
解:
(1)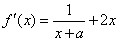 ,依题意有
,依题意有 ,故
,故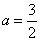 .
.
从而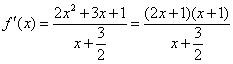 .
.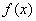 的定义域为
的定义域为 .
.
当 时,
时,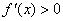 ;
;
当 时,
时,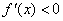 ;
;
当 时,
时,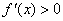 .
.
从而,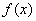 分别在区间
分别在区间 单调递增,在区间
单调递增,在区间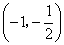 单调递减.
单调递减.
(2) 的定义域为
的定义域为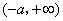 ,
,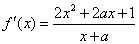 .
.
方程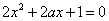 的判别式
的判别式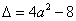 .
.
(i)若 ,即
,即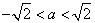 ,在
,在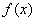 的定义域内
的定义域内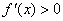 ,故
,故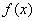 无极值.
无极值.
(ⅱ)若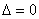 ,则
,则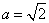 或
或 .
.
若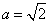 ,
, ,
,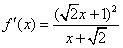 .
.
当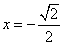 时,
时,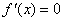 ,
,
当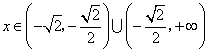 时,
时, ,所以
,所以 无极值.
无极值.
若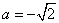 ,
,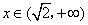 ,
,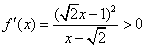 ,
,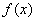 也无极值.
也无极值.
(ⅲ)若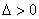 ,即
,即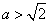 或
或 ,则
,则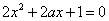 有两个不同的实根
有两个不同的实根
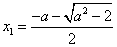 ,
, .
.
当 时,
时,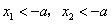 ,从而
,从而 在
在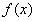 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当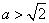 时,
时,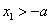 ,
,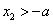 ,
, 在
在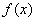 的定义域内有两个不同的零点,由极值判别方法知
的定义域内有两个不同的零点,由极值判别方法知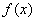 在
在 取得极值.
取得极值.
综上,f(x)存在极值时,a的取值范围为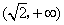 .
.
f(x)的极值之和为:
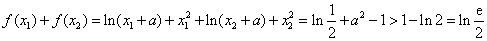 .
.
点评:
本题主要考查函数的导数、极值、单调区间的求法,考查利用导数和函数知识解综合问题的能力.
求函数的单调区间,因函数的单调性可能是单调递增也可能是单调递减所以要讨论,其实质就是讨论导数的符号.
一般地可导函数的极值存在要求有两个条件:一是方程 在
在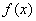 的定义域内有解;二是在方程
的定义域内有解;二是在方程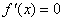 的根的两边导数
的根的两边导数 的符号要相反.因此在利用导数求可导函数的极值时就要分两层讨论.
的符号要相反.因此在利用导数求可导函数的极值时就要分两层讨论.
例5、设函数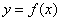 的图象是曲线
的图象是曲线 ,曲线
,曲线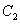 与
与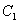 关于直线
关于直线 对称.将曲线
对称.将曲线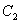 向右平移1个单位得到曲线
向右平移1个单位得到曲线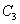 ,已知曲线
,已知曲线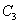 是函数
是函数 的图象.
的图象.
(1)求函数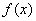 的解析式;
的解析式;
(2)设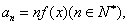 求数列
求数列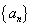 的前
的前 项和
项和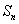 ,并求最小的正实数
,并求最小的正实数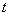 ,使
,使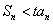 对任意
对任意 都成立.
都成立.
解:
(1)由题意知,曲线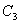 向左平移1个单位得到曲线
向左平移1个单位得到曲线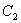 ,∴曲线
,∴曲线 是函数
是函数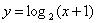 的图象.
的图象.
曲线 与曲线
与曲线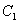 关于直线
关于直线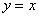 对称,∴曲线
对称,∴曲线 是函数
是函数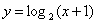 的反函数的图象.
的反函数的图象.
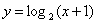 的反函数为
的反函数为 .
. .
.
(2)由题设: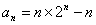 ,
,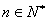
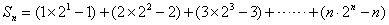
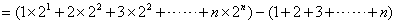
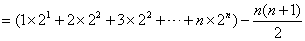 .
.

 .①
.①
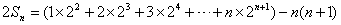 .②
.②
由②—①得,
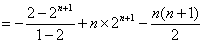
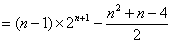 .
.
当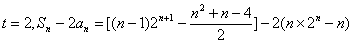
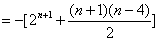 .
.
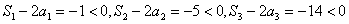 .
.
当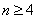 时,
时, .
.
∴当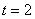 时,对一切
时,对一切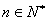 ,
,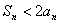 恒成立.
恒成立.
当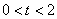 时,
时,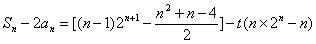
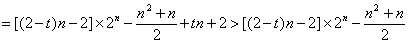 .
.
记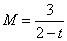 ,则当
,则当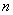 大于比
大于比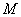 大的正整数时,
大的正整数时,
 .
.
也就证明当 时,存在正整数
时,存在正整数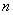 ,使得
,使得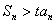 .
.
也就是说当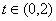 时,
时,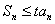 不可能对一切
不可能对一切 都成立.
都成立.
∴t的最小值为2.
例6、(2007·天津)在数列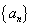 中,
中,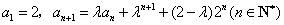 ,其中λ>0.求数列
,其中λ>0.求数列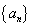 的前
的前 项和
项和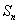 .
.
分析:
数列的通项公式和前 项和的求解,是高考中考查的一个重点内容,对于它们的解决要掌握一些方法.
项和的求解,是高考中考查的一个重点内容,对于它们的解决要掌握一些方法.
解:
由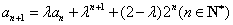 ,
,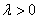 ,可得
,可得
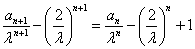 ,
,
所以 为等差数列,其公差为1,首项为0,
为等差数列,其公差为1,首项为0,
故 ,所以数列
,所以数列 的通项公式为
的通项公式为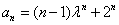 .
.
设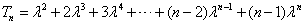 , ①
, ①
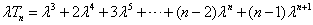 ②
②
当 时,①式减去②式,
时,①式减去②式,
得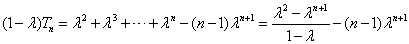 ,
,
 .
.
这时数列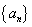 的前
的前 项和
项和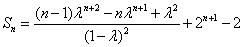 .
.
当 时,
时,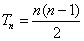 .这时数列
.这时数列 的前
的前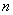 项和
项和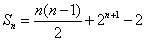 .
.
点评:
本题考查数列的通项公式和前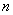 项和.对于等比数列的前
项和.对于等比数列的前 项和公式,由于公比的取值不同而需要分类讨论.
项和公式,由于公比的取值不同而需要分类讨论.
例7、已知函数f(x)=ax+lnx,其中a为实常数,设e为自然对数的底数.
(1)若f(x)在区间(0,e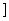 上的最大值为-3,求a的值;
上的最大值为-3,求a的值;
(2)当a=-1时,试推断方程| f(x)|=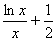 是否有实数解.
是否有实数解.
解:
(1)∵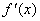 =a+
=a+ ,x∈(0,e),
,x∈(0,e), ∈[
∈[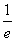 ,+∞
,+∞ .
.
①若a≤-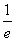 ,则
,则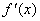 ≥0,从而f(x)在(0,e)上增函数.
≥0,从而f(x)在(0,e)上增函数.
∴f(x)max =f(e)=ae+1≥0.不合题意.
②若a<- ,则由
,则由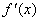 >0
>0 a+
a+ >0,即0<x<-
>0,即0<x<-
由f(x)<0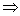 a+
a+ <0,即-
<0,即-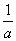 <x≤e.
<x≤e.
∴f(x)max=f(-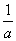 )=-1+ln(-
)=-1+ln(-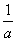 ).
).
令-1+ln(-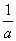 )=-3,则ln(-
)=-3,则ln(- )=-2.∴-
)=-2.∴- =e-2,
=e-2,
即a=-e2. ∵-e2<-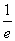 ,∴a=-e2为所求.
,∴a=-e2为所求.
(2)当a=-1时,f(x)=-x+lnx, =-1+
=-1+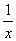 =
= .
.
当0<x<1时,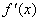 >0;当x>1时,
>0;当x>1时, <0.
<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上减函数.
从而f(x)max=f(1)=-1.∴f(x)=-x+lnx≤-1,从而lnx≤x-1.
令g(x)=|f(x)|-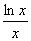 =
= =x-lnx-
=x-lnx-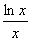 -
-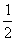 =x-(1+
=x-(1+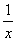 )lnx-
)lnx-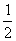
①当0<x<2时,有g(x)≥x-(1+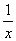 )(x-1)-
)(x-1)-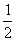 =
= -
-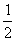 >0.
>0.
②当x≥2时,g′(x)=1-[(- )lnx+(1+
)lnx+(1+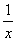 )·
)·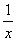 ]=
]=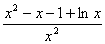
= .
.
∴g(x)在[2,+∞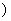 上增函数,∴g(x)≥g(2)=
上增函数,∴g(x)≥g(2)=
综合①、②知,当x>0时,g(x)>0,即|f(x)|>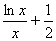 .
.
故原方程没有实解.
例8、已知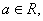 函数
函数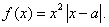
(1)当a=2时,求使f(x)=x成立的x的集合;
(2)求函数y=f (x)在区间[1,2]上的最小值.
解:(1)由题意,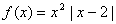 .
.
当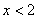 时,由
时,由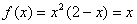 ,解得
,解得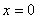 或
或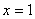 ;
;
当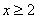 时,由
时,由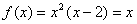 ,解得
,解得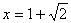 .
.
综上,所求解集为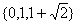 .
.
(2)设此最小值为m.
①当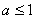 时,在区间[1,2]上,
时,在区间[1,2]上,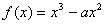 ,
,
因为 ,
,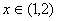 ,
,
则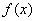 是区间[1,2]上的增函数,所以
是区间[1,2]上的增函数,所以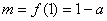 .
.
②当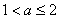 时,在区间[1,2]上,
时,在区间[1,2]上,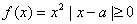 ,由
,由 知
知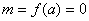 .
.
③当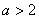 时,在区间[1,2]上,
时,在区间[1,2]上, .
.
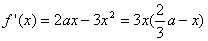 .
.
若 ,在区间(1,2)上,
,在区间(1,2)上,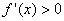 ,则
,则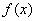 是区间[1,2]上的增函数,所以
是区间[1,2]上的增函数,所以 .
.
若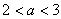 ,则
,则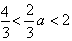 .
.
当 时,
时, ,则
,则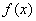 是区间[1,
是区间[1,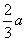 ]上的增函数,
]上的增函数,
当 时,
时, ,则
,则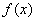 是区间[
是区间[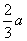 ,2]上的减函数,
,2]上的减函数,
因此当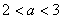 时,
时, 或
或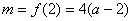 .
.
当 时,
时,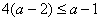 ,故
,故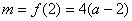 ,
,
当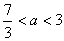 时,
时,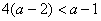 ,故
,故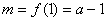 .
.
综上所述,所求函数的最小值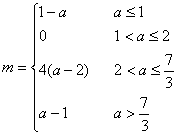
例9、设函数f(x)=x2+|x-a|+1,x∈R.
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的最小值.
解:(1)当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),
此时f(x)为偶函数.
当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1.
f(-a)≠f(a),f(-a)≠-f(a).
此时函数f(x)既不是奇函数,也不是偶函数.
(2)①当x≤a时,函数f(x)=x2-x+a+1=(x- )2+a+
)2+a+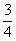 .
.
若a≤ ,则函数f(x)在(-∞,a]上单调递减.
,则函数f(x)在(-∞,a]上单调递减.
从而函数f(x)在(-∞,a 上的最小值为f(a)=a2+1.
上的最小值为f(a)=a2+1.
若a> ,则函数f(x)在(-∞,a
,则函数f(x)在(-∞,a 上的最小值为f(
上的最小值为f(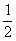 )=
)= +a,且f(
+a,且f( )≤f(a).
)≤f(a).
②当x≥a时,函数f(x)=x2+x-a+1=(x+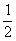 )2-a+
)2-a+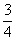 .
.
若a≤-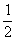 ,则函数f(x)在[a,+∞]上的最小值为f(-
,则函数f(x)在[a,+∞]上的最小值为f(-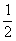 )=
)= -a,且f(-
-a,且f(-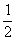 )≤f(a);
)≤f(a);
若a>-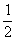 ,则函数f(x)在[a,+∞)单调递增.
,则函数f(x)在[a,+∞)单调递增.
从而函数f(x)在[a,+∞]上的最小值为f(a)=a2+1.
综上,当a≤-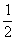 时,函数f(x)的最小值为
时,函数f(x)的最小值为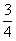 -a;
-a;
当-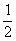 <a≤
<a≤ 时,函数f(x)的最小值是a2+1;
时,函数f(x)的最小值是a2+1;
当a> 时,函数f(x)的最小值是a+
时,函数f(x)的最小值是a+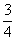 .
.