|
一、复习策略
数学的创新题是相对于传统命题方式而言的,这类题目没有明确的条件或结论,或解题方向不明,自由度大,具有相当大的不确定性,需要通过对问题的观察、分析、类比、归纳等处理过程方能解决,其难度大,要求高,是训练和考查学生的数学思维能力,分析问题和解决问题能力的好题型,数学创新题以“问题”为核心,以“探究”为途径,以“发现”为目的,为高层次思维创造了条件,是挖掘、提练数学思想方法,充分展示应用数学思维方法的良好载体,所以在高考中所占的比重会越来越大。
在高考中的创新题型一般分为三类:第一类是定义信息型创新题;第二类是情景创新题,第三类是类比型创新题,第四类是跨学科型创新题。
二、典例剖析
题型一:定义信息型创新
定义信息型创新题是近几年出现的新题型,因此此类型的背景新颖、构思巧妙,且又能有效地区别学生的思维品质和学习潜力,所以备受师生的青睐,解答这类问题通常分为三大步骤:(1)对新定义进行信息提取,确定归纳的方向;(2)对新定义所提取的信息进行加工,探求解决方法;(3)对定义中提取的知识进行转换,有效的输出,其中对定义信息的提取和化归是解题的关键,也是解题的难点。
例1.(06年广东卷)对于任意的两个实数对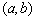 和 和 ,规定: ,规定: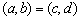 ,当且仅当 ,当且仅当 ;运算“ ;运算“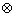 ”为: ”为: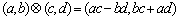 ;运算“ ;运算“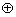 ”为: ”为: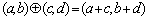 ,设 ,设 ,若 ,若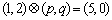 ,则 ,则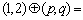 ( ) ( )
A.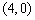 B. B.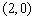
C.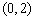 D. D.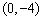
思路分析:按定义求出p,q的值.
解:
由 得 得 , ,
所以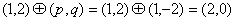 ,故选B. ,故选B.
例2.(06年上海)如图,平面中两条直线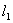 和 和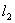 相交于点O,对于平面上任意一点M,若p、q分别是M到直线 相交于点O,对于平面上任意一点M,若p、q分别是M到直线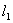 和 和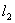 的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题: 的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题:
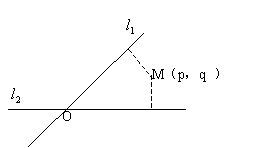
①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;
②若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个;
③若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个.
上述命题中,正确命题的个数是( )
A.0 B.1 C.2 D.3
思路分析:
(p,q)的个数就是到直线l1的距离为p的直线与到直线l2的距离为q的直线的交点的个数,作出满足条件的直线即可.
解:选(D)
①正确,此点为点O;②正确,注意到p,q为常数,由p,q中必有一个为零,另一个非零,从而可知有且仅有2个点,这两点在其中一条直线上,且到另一直线的距离为q(或p);③正确,四个交点为与直线l1相距为p的两条平行线和与直线l2相距为q的两条平行线的交点.
点评:
概念型创新题特点是首先给出一个定义,然后根据定义提出一系列问题.解决此类问题,先要认真理解题目给出的定义,把握定义的本质,在此基础上按定义处理问题.
例3.(07年福建卷)中学数学中存在许多关系,比如“相等关系”、“平行关系”等等.
如果集合A中元素之间的一个关系“~”满足以下三个条件:
(1)自反性:对于任意 ,都有 ,都有 ; ;
(2)对称性:对于 ,若 ,若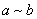 ,则有 ,则有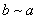 ; ;
(3)传递性:对于 ,若 ,若 , ,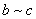 ,则有 ,则有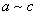 . .
则称“~”是集合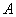 的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______. 的一个等价关系.例如:“数的相等”是等价关系,而“直线的平行”不是等价关系(自反性不成立).请你再列出三个等价关系:______.
解:
答案不唯一,如“图形的全等”、“图形的相似”、 “非零向量的共线”、“命题的充要条件”等等.
例4.(06年福建卷)对于直角坐标平面内的任意两点A(x1, y1)、B(x2,y2),定义它们之间的一种“距离”:‖AB‖=|x1-x2|+|y1-y2|.给出下列三个命题: y1)、B(x2,y2),定义它们之间的一种“距离”:‖AB‖=|x1-x2|+|y1-y2|.给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖2+‖CB‖2=‖AB‖2;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题为___________.
解:
对于直角坐标平面内的任意两点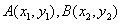 ,定义它们之间的一种“距离”:‖AB‖=|x1-x2|+|y1-y2|, ,定义它们之间的一种“距离”:‖AB‖=|x1-x2|+|y1-y2|,
①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则
 = =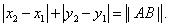
③在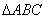 中, 中,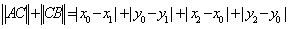
>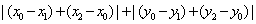 = =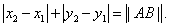
∴命题①③成立,而命题②在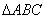 中,若 中,若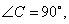 则 则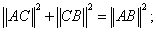 明显不成立. 明显不成立.
则应填①③.
例5.(07北京)已知集合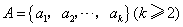 ,其中 ,其中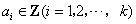 ,由 ,由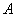 中的元素构成两个相应的集合: 中的元素构成两个相应的集合:
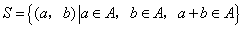 , ,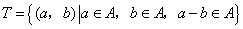 . .
其中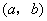 是有序数对,集合S和T中的元素个数分别为m和n.若对于任意的 是有序数对,集合S和T中的元素个数分别为m和n.若对于任意的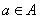 ,总有 ,总有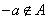 ,则称集合A具有性质P. ,则称集合A具有性质P.
(I)检验集合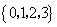 与 与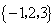 是否具有性质P,并对其中具有性质P的集合,写出相应的集合S和T; 是否具有性质P,并对其中具有性质P的集合,写出相应的集合S和T;
(II)对任何具有性质P的集合A,证明: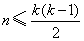 ; ;
(III)判断m和n的大小关系,并证明你的结论.
(I)解:集合 不具有性质P.集合 不具有性质P.集合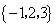 具有性质P, 具有性质P,
其相应的集合S和T是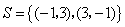 , ,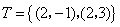 . .
(II)证明:
首先,由A中元素构成的有序数对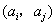 共有 共有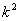 个. 个.
因为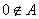 ,所以 ,所以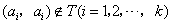 ; ;
又因为当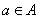 时, 时, 时, 时,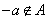 ,所以当 ,所以当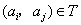 时, 时,
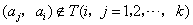 . .
从而,集合T中元素的个数最多为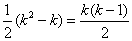 ,即 ,即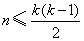 . .
(III)解:m=n,证明如下:
(1)对于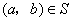 ,根据定义, ,根据定义,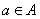 , , ,且 ,且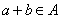 ,从而 ,从而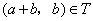 . .
如果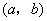 与 与 是S的不同元素,那么 是S的不同元素,那么 与 与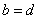 中至少有一个不成立, 中至少有一个不成立,
从而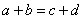 与 与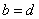 中也至少有一个不成立. 中也至少有一个不成立.
故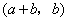 与 与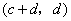 也是T的不同元素. 也是T的不同元素.
可见,S中元素的个数不多于T中元素的个数,即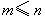 , ,
(2)对于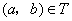 ,根据定义, ,根据定义,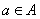 , ,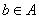 ,且 ,且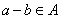 ,从而 ,从而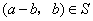 . .
如果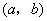 与 与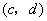 是T的不同元素,那么 是T的不同元素,那么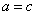 与 与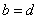 中至少有一个不成立, 中至少有一个不成立,
从而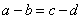 与 与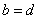 中也不至少有一个不成立, 中也不至少有一个不成立,
故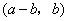 与 与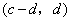 也是S的不同元素. 也是S的不同元素.
可见,T中元素的个数不多于S中元素的个数,即 , ,
由(1)(2)可知,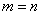 . .
例6.设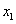 、 、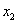 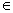 R,常数 R,常数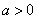 .定义运算“ .定义运算“ ”: ”: . .
(1)若 求动点 求动点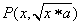 轨迹C的方程; 轨迹C的方程;
(2)若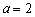 ,不过原点的直线l与x轴、y轴的交点分别为T、S,并且与(1)中轨迹C交于不同的两点P、Q ,试求 ,不过原点的直线l与x轴、y轴的交点分别为T、S,并且与(1)中轨迹C交于不同的两点P、Q ,试求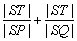 的取值范围; 的取值范围;
(3)设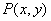 是平面上的任一点,定义 是平面上的任一点,定义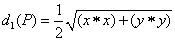 、 、
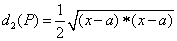 .若在(1)中轨迹C上存在不同的两点A1、A2,使得 .若在(1)中轨迹C上存在不同的两点A1、A2,使得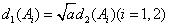 成立,求实数a的取值范围. 成立,求实数a的取值范围.
解答:
(1)设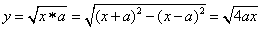 , ,
又由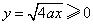 ,可得动点 ,可得动点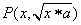 轨迹C的方程为: 轨迹C的方程为: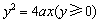 . .
(2)由题得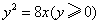 ,设直线 ,设直线 ,依题意 ,依题意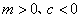 ,则 ,则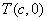 . .
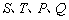 都在直线l上,则 都在直线l上,则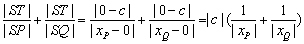 . .

由题,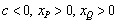 ,∴ ,∴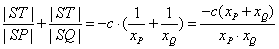 . .
由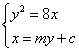 消去 消去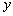 得, 得, . .
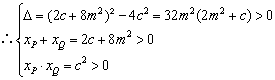
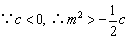
代入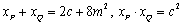 得, 得,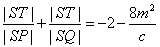 , ,
又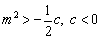 知, 知,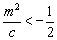 ,所以 ,所以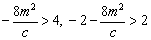 . .
即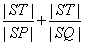 的取值范围是 的取值范围是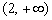 . .
(3)由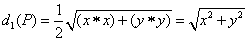 , ,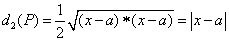 , ,
设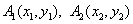 ,依题意则有, ,依题意则有,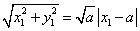 且 且 , ,
又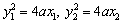 ,即 ,即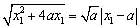 且 且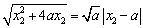 , ,
故方程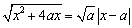 在 在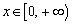 有两个不等的实数解. 有两个不等的实数解.
平方整理有,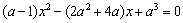 在 在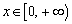 有两个不等的实数解. 有两个不等的实数解.
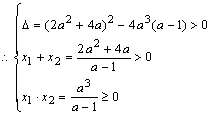 又 又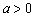 ,得 ,得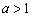 . .
故实数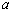 的取值范围是 的取值范围是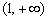 . .
题型二:情境创新题
这一类问题,往往出现在一个较新的背景之下,题型新颖,形式多样,融综合性、应用性、开放性、创新性于一体.可以较好的考查学生的学习能力,阅读理解能力,数学思维能力等.由于突出体现了“考思维能力与创新意识”这一特色,所以,在近几年的高考中,备受命题者的青睐.
例7.(06陕西卷)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
A.4,6,1,7 B.7,6,1,4
C.6,4,1,7 D.1,6,4,7
思路分析:本题的本质是一种对应,根据对应法则求出a,b,c,d的值.
解:当接收方收到密文14,9,23,28时,
则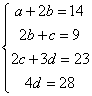 ,解得 ,解得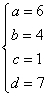 ,解密得到的明文为C. ,解密得到的明文为C.
例8.某娱乐中心有如下摸奖活动:拿8个白球和8个黑球放在一盒中,规定:凡摸奖者,每人每次交费1元,每次从盒中摸出5个球,中奖情况为:摸出5个白球中20元,摸出4个白球1个黑球中2元,摸出3个白球2个黑球中价值为0.5元的纪念品1件,其他无任何奖励.
(1)分别计算中奖20元、2元的概率;
(2)若有1560人次摸奖,不计其他支出,用概率估计该中心收入多少钱?
思路分析:本题是等可能事件的概率问题,用等可能事件的概率公式求解.
解:
(1)由已知中奖20元的概率P1=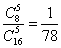 ;中奖2元的概率P2= ;中奖2元的概率P2=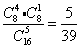 ; ;
中奖0.5元的概率P3=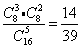 . .
(2)由(1)知体彩中心收费为1560元,付出
1560×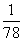 ×20+1560× ×20+1560× ×2+1560× ×2+1560×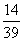 ×0.5=1080元, ×0.5=1080元,
收入=1560-1080=480元.
故知中奖20元、2元的概率分别为: 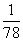 、 、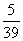 ;估计该中心收入480元. ;估计该中心收入480元.
点评:
概率问题是高考命题的主干知识,涉及到的问题情景是常考常新的,多数是与生活实际和生产实际相关联的.
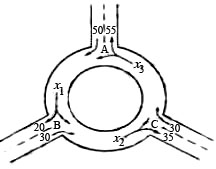
例9.(06年北京卷)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 的机动车辆数如图所示,图中 的机动车辆数如图所示,图中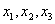 分别表示该时段单位时间通过路段 分别表示该时段单位时间通过路段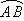 、 、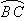 、 、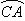 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( ) 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则( )
A.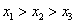 B. B.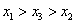
C.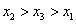 D. D.
解:
依题意,有x1=50+x3-55=x3-5,∴x1<x3,同理,x2=30+x1-20=x1+10,
∴x1<x2,同理,x3=30+x2-35=x2-5,∴x3<x2,故选C.
例10.这是一个计算机程序的操作说明:
(1)初始值为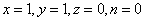 ; ;
(2)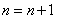 (将当前 (将当前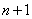 的值赋予新的 的值赋予新的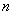 ); );
(3)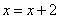 (将当前 (将当前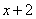 的值赋予新的 的值赋予新的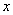 ); );
(4)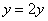 (将当前 (将当前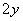 的值赋予新的 的值赋予新的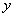 ); );
(5) (将当前 (将当前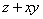 的值赋予新的 的值赋予新的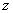 ); );
(6)如果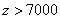 ,则执行语句(7),否则回语句(2)继续进行; ,则执行语句(7),否则回语句(2)继续进行;
(7)打印 ; ;
(8)程序终止.
由语句(7)打印出的数值为_____________,_____________ .
请写出计算过程:
点拨与提示:
我们不难看出,该问题是一个循环、迭代的过程.为了更好的理解题意,我们不妨按照这个程序操作几次:
| |
n |
x |
y |
z |
判断 |
初始值 |
0 |
1 |
1 |
0 |
z<7000,返回(2) |
一轮操作 |
1 |
3 |
2 |
5 |
z<7000,返回(2) |
二轮操作 |
2 |
5 |
4 |
25 |
z<7000,返回(2) |
三轮操作 |
3 |
7 |
8 |
81 |
z<7000,返回(2) |
…… |
…… |
就此操作下去,并不难得出答案,这也是本题的一种计算方法.
从另一个角度考虑,本题中我们比较难以理解的是这样的语句:“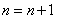 ; ;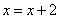 ;……”,虽然题目中已经给出很好的解释,但是,按照我们通常的认识,应该用不同的符号来分别表达新值与旧值,如何从数学上较好的体现新值与旧值之间的不同,以及它们之间的联系呢?事实上注意到在整个计算的过程中,一方面,n的值似乎只起到一个计算第几轮的作用,另一方面,随着n的变化, ;……”,虽然题目中已经给出很好的解释,但是,按照我们通常的认识,应该用不同的符号来分别表达新值与旧值,如何从数学上较好的体现新值与旧值之间的不同,以及它们之间的联系呢?事实上注意到在整个计算的过程中,一方面,n的值似乎只起到一个计算第几轮的作用,另一方面,随着n的变化,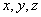 的值随之变化.从这一个角度,不难想到,数列是一种较好的表示方法. 的值随之变化.从这一个角度,不难想到,数列是一种较好的表示方法.
答案: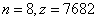
题型三:类比归纳型创新题
类比归纳题型可锻炼学生的创造性思维,培养学生的创新精神和创造力,又因为其思维含量高、知识覆盖面广,综合性强、难度大,而且命题形式丰富多彩,因而备受高考命题者的青睐。“由特殊到一般”是解决这类题型的思维主线,主要类型有:
(1)研究命题本身,对命题进行拓展,我们所熟悉的“观察——归纳——猜想——证明”是解决这类问题的常用方法,对命题拓展时要注意它们外在的形式特征,抓住规律性的东西。
(2)解决问题的方法,对命题进行论证,对于给出的一般性结论,我们可先研究其简单的情形,通过类比归纳,探索出解决问题的方法。
(3)穷举归纳,完善命题,可能的情形如果不是太多,即可通过全部列出的方法解决问题。
例11.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题可以得到命题__________,这个命题的真假性是______ .
解:
“如果两个二面角的两个半平面分别对应垂直,那么这两个二面角的平面角相等或互补”.当两棱不平行不成立,所以,这个命题是错误的.
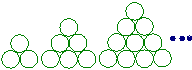
例12.在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第一堆只有一层,就一个乒乓球;第2、3、4…堆最底层(第一层)分别按如图所示方式固定摆放,从第一层开始,每层的小球自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示第n堆的乒乓球总数,则f(3)=________;f(n)=__________.(答案用n表示).
解析:
f(3)=1+(1+2)+(1+2+3)=10,
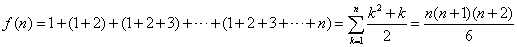 . .
例13.已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值. 试对双曲线C′: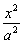 - -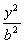 =1写出具有类似特性的性质,并加以证明. =1写出具有类似特性的性质,并加以证明.
解:
类似的性质为若MN是双曲线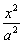 - -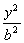 =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值. =1上关于原点对称的两个点,点P是双曲线上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.
设点M的坐标为(m,n),
则点N的坐标为(-m,-n),
其中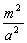 - -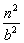 =1 =1
又设点P的坐标为(x,y),
由kPM=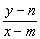 ,kPN= ,kPN=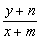 , ,
得kPM·kPN=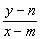 · ·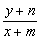 = =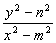 , ,
将y2=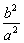 x2-b2,n2= x2-b2,n2=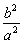 m2-b2,代入得kPM·kPN= m2-b2,代入得kPM·kPN=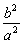 . .
点评:
本题主要考查椭圆、双曲线的基本性质,考查类比、归纳、探索问题的能力,它是一道综合椭圆和双曲线基本知识的综合性题目,对思维能力有较高的要求.
例14.(2000上海)规定 ,其中x∈R,m是正整数,且 ,其中x∈R,m是正整数,且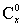 =1,这是组合数 =1,这是组合数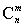 (n、m是正整数,且m≤n的一种推广). (n、m是正整数,且m≤n的一种推广).
(1)求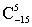 的值; 的值;
(2)组合数的两个性质:
①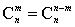 . ② . ②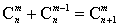 . .
是否都能推广到 (x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出证明;若不能,则说明理由. (x∈R,m是正整数)的情形?若能推广,请写出推广的形式,并给出证明;若不能,则说明理由.
(3)已知组合数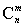 是正整数,证明:当x∈Z,m是正整数时, 是正整数,证明:当x∈Z,m是正整数时,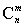 ∈Z. ∈Z.
(1)解: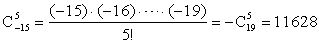 . .
(2)解:性质①不能推广.例如当x=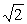 时, 时,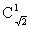 有定义,但 有定义,但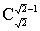 无意义;性质②能推广,它的推广形式是 无意义;性质②能推广,它的推广形式是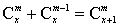 ,x∈R,m是正整数,事实上 ,x∈R,m是正整数,事实上
当m=1时,有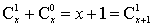 , ,
当m≥2时,
 . .
(3)证明:当x≥m时,组合数 ∈Z. ∈Z.
当0≤x<m时,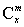 =0∈Z. =0∈Z.
当x<0时,∵-x+m-1>0,
∴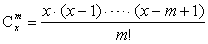
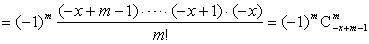 ∈Z. ∈Z.
题型四:学科间综合创新问题
学科间综合创新题注重了数学的现实性与时代性,关注生活、关注热点,命题呈现题意新颖、题型创新的特点,跨学科的题目通常与物理、化学、生物等学科交叉。解决这一类题目的关键是从题目中构造数学模型,利用数学知识来解决。通常用到的数学知识有函数、数列、不等式、概率等。
例15.一个人以6米/秒的速度去追停在交通灯前的汽车,当他离汽车25米时,交通灯由红变绿,汽车以1米 / 秒2的加速度匀加速开走,那么( )
A.人可在7米内追上汽车
B.人可在10米内追上汽车
C.人追不上汽车,其间距离最近为5米
D.人追不上汽车,其间距离最近为7米
思路分析:
本题是一道加速行程问题,需要运用物理现象建立数学模型,即汽车行程+25=人的行程,建立二次函数关系式.
解:
若经t秒人刚好追上汽车,则S+25=6 t ,由S= 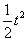 ,得 ,得
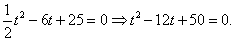
考虑距离差 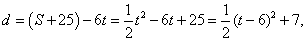
故当t = 6时,d 有最小值7 ,即人与汽车最少相距7米,故选D.
点评:
本题属于跨学科综合题,要求将物理问题抽象成数学问题,利用数学工具,通过推理和计算解决物理问题,这类题型也是今后数学高考命题的趋势之一.
例16.给出下列一系列化合物的分子式: 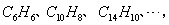 则该系列化合物中,分子中含碳元素的质量分数最大可无限接近( ) 则该系列化合物中,分子中含碳元素的质量分数最大可无限接近( )
A. 95% B. 96% C. 97% D.98%
点拨与提示:C与H的下标分别成等差数列,求出通式,利用极限的知识求解.
答案:B
- 返回 -
|