|
一、复习策略
1、函数的最值问题是其他最值问题的基础之一,许多最值问题最后总是转化为函数(特别是二次函数)的最值问题.求函数最值的方法有:配方法、均值不等式法、单调性、导数法、判别式法、有界性、图象法等.
2、求几类重要函数的最值方法;
(1)二次函数:配方法和函数图像相结合;
(2)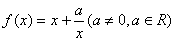 :均值不等式法和单调性加以选择; :均值不等式法和单调性加以选择;
(3)多元函数:数形结合或转化为一元函数.
3、三角函数、数列、解析几何中的最值问题,往往将问题转化为函数问题,利用求函数最值的方法或基本不等式法求解.
4、实际应用问题中的最值问题一般有下列两种模型:直接法,目标函数法(线性规划,二次函数的最值).
5、不等式恒成立问题常转化为求函数的最值问题.f(x)>m恒成立,即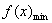 >m;f(x)<m恒成立,即 >m;f(x)<m恒成立,即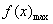 <m. <m.
6、参数范围问题内容涉及代数和几何的多个方面,解题的关键是不等关系的建立,其途径多多,诸如判别式法,均值不等式法,变量的有界性法,函数的性质法,数形结合法等等.解决这一类问题,常用的思想方法有:函数思想、数形结合等.
二、典例剖析
问题1:函数的最值问题
例1、(07江苏卷)已知二次函数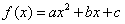 的导数为 的导数为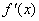 , ,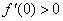 ,对于任意实数 ,对于任意实数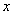 ,都有 ,都有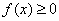 ,则 ,则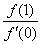 的最小值为( ) 的最小值为( )
A.3 B.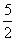 C.2 D. C.2 D.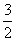
解:
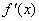 = =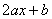 ,依题意,有: ,依题意,有: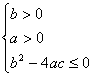 ,可得 ,可得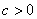 , ,
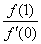 = =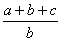 = =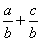 +1≥2 +1≥2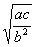 +1≥2 +1≥2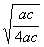 +1=2,故选(C). +1=2,故选(C).
例2、如下图(1)所示,定义在D上的函数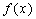 ,如果满足:对任意 ,如果满足:对任意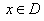 ,存在常数A,都有 ,存在常数A,都有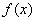 ≥A成立,则称函数 ≥A成立,则称函数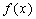 在D上有下界,其中A称为函数的下界. (提示:图(1)、(2)中的常数A、B可以是正数,也可以是负数或零) 在D上有下界,其中A称为函数的下界. (提示:图(1)、(2)中的常数A、B可以是正数,也可以是负数或零)
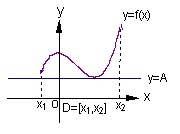 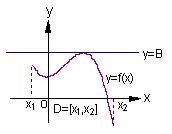
(1) (2)
(Ⅰ)试判断函数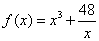 在(0,+ 在(0,+ )上是否有下界?并说明理由; )上是否有下界?并说明理由;
(Ⅱ)又如具有上右图(2)特征的函数称为在D上有上界.请你类比函数有下界的定义,给出函数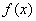 在D上有上界的定义,并判断(Ⅰ)中的函数在(- 在D上有上界的定义,并判断(Ⅰ)中的函数在(- , 0)上是否有上界?并说明理由; , 0)上是否有上界?并说明理由;
(Ⅲ)已知某质点的运动方程为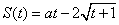 ,要使在 ,要使在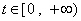 上的每一时刻该质点的瞬时速度是以A= 上的每一时刻该质点的瞬时速度是以A=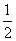 为下界的函数,求实数a的取值范围. 为下界的函数,求实数a的取值范围.
分析:
利用导数判断函数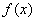 的单调性,求出函数 的单调性,求出函数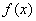 的最值,从而可以确定函数的下界或上界;或用重要不等式求最值. 的最值,从而可以确定函数的下界或上界;或用重要不等式求最值.
解:
(Ⅰ)解法1:∵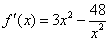 ,由 ,由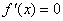 得 得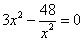 , ,
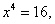 ∵ ∵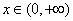 ,∴x=2, ,∴x=2,
∵当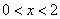 时, 时,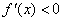 ,∴函数 ,∴函数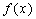 在(0,2)上是减函数; 在(0,2)上是减函数;
当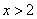 时, 时,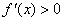 ,∴函数 ,∴函数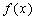 在(2,+ 在(2,+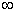 )上是增函数; )上是增函数;
∴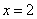 是函数在区间(0,+ 是函数在区间(0,+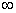 )上的最小值点, )上的最小值点,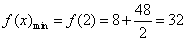 . .
∴对任意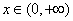 ,都有 ,都有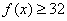 , ,
即在区间(0,+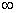 )上存在常数A=32,使得对任意 )上存在常数A=32,使得对任意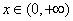 都有 都有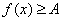 成立, 成立,
∴函数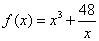 在(0,+ 在(0,+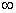 )上有下界. )上有下界.
解法2: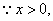 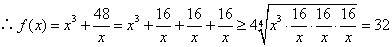 . .
当且仅当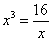 即x=2时“=”成立. 即x=2时“=”成立.
∴对任意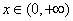 ,都有 ,都有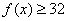 , ,
即在区间(0,+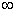 )上存在常数A=32,使得对任意 )上存在常数A=32,使得对任意 都有 都有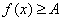 成立, 成立,
∴函数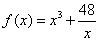 在(0,+ 在(0,+ )上有下界. )上有下界.
(Ⅱ)类比函数有下界的定义,函数有上界可以这样定义:
定义在D上的函数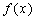 ,如果满足:对任意 ,如果满足:对任意 ,存在常数B,都有 ,存在常数B,都有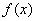 ≤B成立,则称函数 ≤B成立,则称函数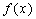 在D上有上界,其中B称为函数的上界. 在D上有上界,其中B称为函数的上界.
设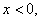  则 则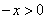 ,由(Ⅰ)知,对任意 ,由(Ⅰ)知,对任意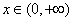 ,都有 ,都有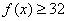 , ,
∴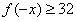 ,∵函数 ,∵函数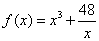 为奇函数,∴ 为奇函数,∴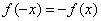 . .
∴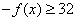 ,∴ ,∴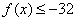 . .
即存在常数B=-32,对任意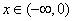 ,都有 ,都有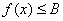 , ,
∴函数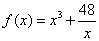 在(- 在(-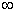 ,0)上有上界. ,0)上有上界.
(Ⅲ)质点在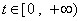 上的每一时刻的瞬时速度 上的每一时刻的瞬时速度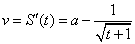 . .
依题意得对任意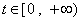 有 有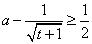 . .
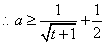 对任意 对任意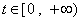 恒成立. 恒成立.
令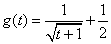 ,∵函数 ,∵函数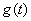 在[0,+∞)上为减函数. 在[0,+∞)上为减函数.
∴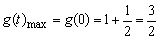 . .
∴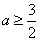 . .
问题2:三角函数、数列、解析几何中的最值问题
将问题转化为函数问题,利用求函数最值的方法求解.
例3、(05年上海)点A、B分别是椭圆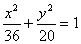 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于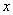 轴上方,PA⊥PF. 轴上方,PA⊥PF.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
分析:
将d用点M的坐标表示出来,
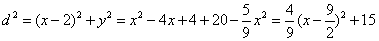 ,然后求其最小值. ,然后求其最小值.
解:
(1)由已知可得点A(-6,0),F(4,0).
设点P(x,y),则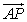 ={x+6,y}, ={x+6,y},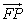 ={x-4,y},由已知可得 ={x-4,y},由已知可得
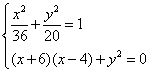 ,则2x2+9x-18=0,解得x= ,则2x2+9x-18=0,解得x=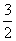 或x=-6. 或x=-6.
由于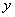 >0,只能 >0,只能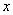 = =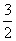 ,于是 ,于是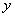 = =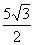 .∴点P的坐标是( .∴点P的坐标是(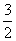 , ,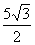 ). ).
(2) 直线AP的方程是x-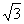 y+6=0. y+6=0.
设点M(m,0),则M到直线AP的距离是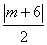 . .
于是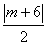 = =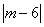 ,又-6≤m≤6,解得m=2. ,又-6≤m≤6,解得m=2.
椭圆上的点(x,y)到点M的距离d有
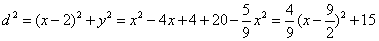 , ,
由于-6≤x≤6,∴当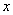 = =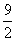 时,d取得最小值 时,d取得最小值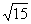 . .
例4、(05年辽宁)如图,在直径为1的圆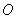 中,作一关于圆心对称、邻边互相垂直的十字形,其中 中,作一关于圆心对称、邻边互相垂直的十字形,其中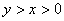 . .
(Ⅰ)将十字形的面积表示为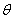 的函数; 的函数;
(Ⅱ)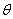 为何值时,十字形的面积最大?最大面积是多少? 为何值时,十字形的面积最大?最大面积是多少?
分析:
将十字型面积S用变量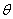 表示出来,转化为三角函数的极值问题,利用三角函数知识求出S的最大值. 表示出来,转化为三角函数的极值问题,利用三角函数知识求出S的最大值.
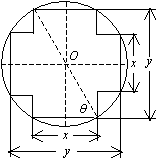
(Ⅰ)解:设S为十字形的面积,则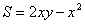 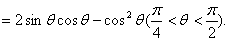
(Ⅱ)解法一:
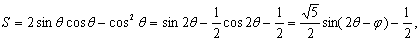
其中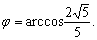 当 当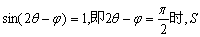 最大. 最大.
所以,当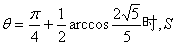 最大. S的最大值为 最大. S的最大值为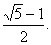
解法二:因为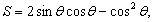
所以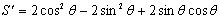 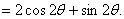 令S′=0, 令S′=0,
即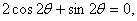 可解得 可解得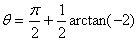 , ,
所以,当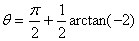 时,S最大,S的最大值为 时,S最大,S的最大值为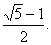
例5、已知点A(-1,0),B(1,-1)和抛物线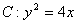 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图. ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
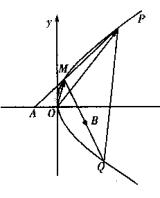
(I)若△POM的面积为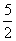 ,求向量 ,求向量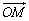 与 与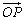 的夹角; 的夹角;
(II)试探求点O到直线PQ的距离是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
分析:
可先设出M与P点的坐标,再利用斜率相等求出 的值,利用向量的数量积求出夹角.第二问中可用重要不等式求出最值. 的值,利用向量的数量积求出夹角.第二问中可用重要不等式求出最值.
解:
(I)设点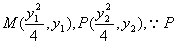 、M、A三点共线, 、M、A三点共线,
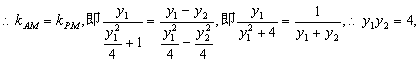
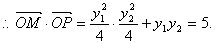
设∠POM=α,则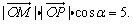
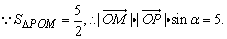 由此可得tanα=1. 由此可得tanα=1.
又

令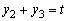 ,则 ,则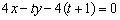 . .
∴O到PQ的距离: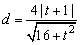 , ,
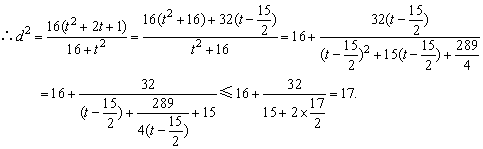
即当且仅当t=16时取最大值,且最大值为 . .
故存在最大值,且最大值为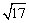 . .
问题3:最值的实际应用
在数学应用性问题中经常遇到有关用料最省、成本最低、利润最大等问题,可考虑建立目标函数,转化为求函数的最值.
例6、(06年江苏卷)请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如下图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
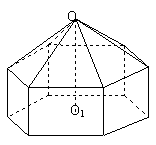
分析:将帐蓬的体积用x表示(即建立目标函数),然后求其最大值.
解:
设OO1为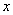 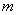 ,则 ,则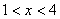 . .
由题设可得正六棱锥底面边长为: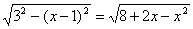 ,(单位: ,(单位: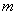 ) )
故底面正六边形的面积为: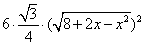 = =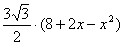 ,(单位: ,(单位: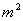 ) )
帐篷的体积为:
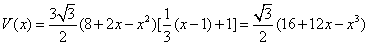 (单位: (单位: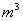 ) )
求导得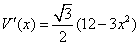 . .
令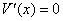 ,解得 ,解得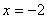 (不合题意,舍去), (不合题意,舍去),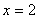 , ,
当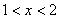 时, 时,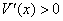 , ,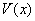 为增函数; 为增函数;
当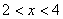 时, 时,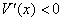 , ,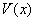 为减函数. 为减函数.
∴当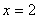 时, 时,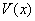 最大. 最大.
答:当OO1为2m时,帐篷的体积最大,最大体积为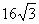 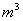 . .
点评:
本题主要考查利用导数研究函数的最值的基础知识,以及运用数学知识解决实际问题的能力.
例7、(05年湖南)对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: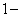  )为0.8,要求洗完后的清洁度是0.99,有两种方案可供选择.方案甲:一次清洗;方案乙:分两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为 )为0.8,要求洗完后的清洁度是0.99,有两种方案可供选择.方案甲:一次清洗;方案乙:分两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为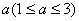 .设用 .设用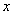 单位质量的水初次清洗后的清洁度是 单位质量的水初次清洗后的清洁度是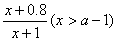 .用 .用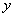 单位质量的水第二次清洗后的清洁度是 单位质量的水第二次清洗后的清洁度是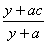 ,其中 ,其中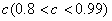 是该物体初次清洗后的清洁度. 是该物体初次清洗后的清洁度.
(1)分别求出方案甲以及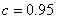 时方案乙的用水量,并比较哪一种方法用水量较小. 时方案乙的用水量,并比较哪一种方法用水量较小.
(2)若采用方案乙,当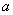 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论 为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论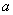 取不同数值时对最少总用水量多少的影响. 取不同数值时对最少总用水量多少的影响.
点拨与提示:
(1)设初次与第二次清洗的用水量分别为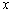 与 与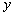 , ,
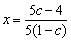 , ,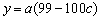 . .
于是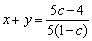 + +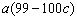 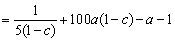 ,利用均值不等式求最值. ,利用均值不等式求最值.
方案甲与方案乙的用水量分别为x与z,由题设有 ,解得x=19,由c=0.95得方案乙初次用水量为3,第二次用水量y满足方程: ,解得x=19,由c=0.95得方案乙初次用水量为3,第二次用水量y满足方程: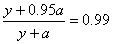 ,解得y=4a,故z=4a+3,即两种方案的用水量分别为19与4a+3,因为当1≤a≤ 3时,x-z=4(4-a)>0,即x>z.故方案乙的用水量较少. ,解得y=4a,故z=4a+3,即两种方案的用水量分别为19与4a+3,因为当1≤a≤ 3时,x-z=4(4-a)>0,即x>z.故方案乙的用水量较少.
(2)设初次与第二次清洗的用水量分别为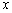 与 与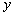 ,类似(I)得 ,类似(I)得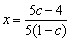 , ,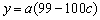 (*) (*)
于是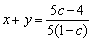 + +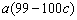  . .
当a为定值时,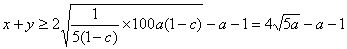 . .
当且仅当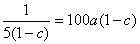 时等号成立,此时 时等号成立,此时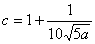 (不合题意,舍去)或 (不合题意,舍去)或 . .
将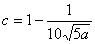 代入(*)得 代入(*)得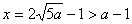 , ,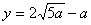 . .
故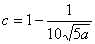 时用水量最少,此时第一次与第二次用水量分别为 时用水量最少,此时第一次与第二次用水量分别为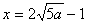 与 与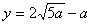 ,最少总用水量为 ,最少总用水量为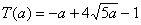 . .
当1≤a≤3时,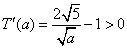 ,故T(a)是增函数(也可用二次函数的单调性来判断),这说明随着a的值的增加,最少总用水量增加. ,故T(a)是增函数(也可用二次函数的单调性来判断),这说明随着a的值的增加,最少总用水量增加.
问题4:恒成立问题
不等式恒成立问题常转化为求函数的最值问题.f(x)>m恒成立,即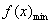 >m; >m;
f(x)<m恒成立,即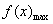 <m. <m.
例8、已知函数f(x)=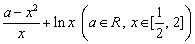 . .
(Ⅰ)当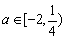 时,求 时,求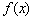 的最大值; 的最大值;
(Ⅱ) 设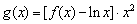 , ,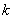 是 是 图象上不同两点的连线的斜率,是否存在实数 图象上不同两点的连线的斜率,是否存在实数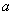 ,使得 ,使得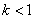 恒成立?若存在,求 恒成立?若存在,求 的取值范围;若不存在,请说明理由. 的取值范围;若不存在,请说明理由.
分析:
利用导数求出函数 的单调性,再比较其极大值与端点值的大小求出 的单调性,再比较其极大值与端点值的大小求出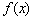 的最大值. 的最大值.
解:
(Ⅰ)当-2≤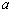 < <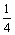 时,由 时,由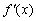 =0得x1= =0得x1=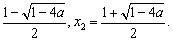
显然-1≤x1<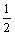 , ,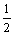 <x2≤2, <x2≤2,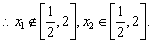
又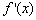 =- =-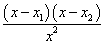 . .
当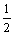 ≤x≤x2时, ≤x≤x2时,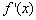 ≥0, ≥0,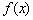 单调递增; 单调递增;
当x2<x≤2时,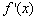 <0, <0,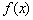 单调递减, 单调递减,
∴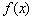 max= max=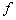 (x2)= (x2)=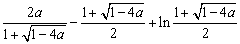
=-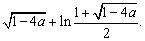
(Ⅱ)答:存在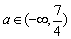 符合条件. 符合条件.
解:因为 = =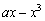 . .
不妨设任意不同两点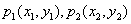 ,其中 ,其中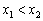 . .
则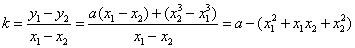 . .
由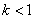 知: 知: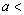 1+ 1+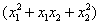 <1 <1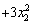 . .
又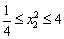 ,故 ,故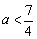 . .
故存在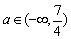 符合条件. 符合条件.
解法二:据题意在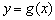 图象上总可以找一点 图象上总可以找一点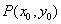 ,使以P为切点的切线平行于图象上任意两点的连线,即存在 ,使以P为切点的切线平行于图象上任意两点的连线,即存在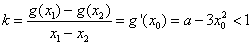 . .
 故存在 故存在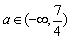 符合条件. 符合条件.
问题五:参数的取值范围问题
参数范围的问题,内容涉及代数和几何的多个方面,综合考查学生应用数学知识解决问题的能力.在历年高考中占有较稳定的比重.解决这一类问题,常用的思想方法有:函数思想、数形结合等.
例9、设直线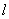 过点P(0,3)且和椭圆 过点P(0,3)且和椭圆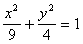 顺次交于A、B两点,求 顺次交于A、B两点,求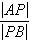 的取值范围. 的取值范围.
分析:
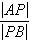 = =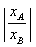 .要求 .要求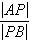 的取值范围,一是构造所求变量 的取值范围,一是构造所求变量 关于某个参数(自然的想到“直线AB的斜率k”)的函数关系式(或方程),通过求函数的值域来达到目的.二是构造关于所求量的一个不等关系,由判别式非负可以很快确定 关于某个参数(自然的想到“直线AB的斜率k”)的函数关系式(或方程),通过求函数的值域来达到目的.二是构造关于所求量的一个不等关系,由判别式非负可以很快确定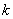 的取值范围,于是问题转化为如何将所求量与 的取值范围,于是问题转化为如何将所求量与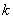 联系起来.韦达定理总是充当这种问题的桥梁,但本题无法直接应用韦达定理,原因在于 联系起来.韦达定理总是充当这种问题的桥梁,但本题无法直接应用韦达定理,原因在于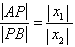 不是关于 不是关于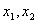 的对称式.问题找到后,解决的方法自然也就有了,即我们可以构造关于 的对称式.问题找到后,解决的方法自然也就有了,即我们可以构造关于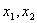 的对称式: 的对称式: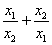 .由此出发,可得到下面的两种解法. .由此出发,可得到下面的两种解法.
解法1:
当直线 垂直于x轴时,可求得 垂直于x轴时,可求得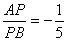 ; ;
当l与x轴不垂直时,设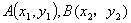 ,直线 ,直线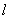 的方程为: 的方程为: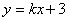 ,代入椭圆方程,消去 ,代入椭圆方程,消去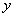 得 得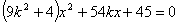 . .
解之得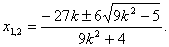
由椭圆关于y轴对称,且点P在y轴上,所以只需考虑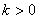 的情形. 的情形.
当 时, 时,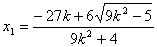 , ,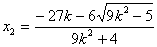 , ,
所以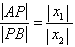 = = = =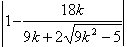 = =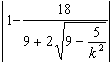 . .
由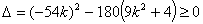 ,解得 ,解得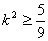 , ,
所以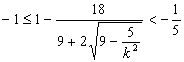 ,即 ,即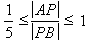 . .
解法2:
设直线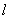 的方程为: 的方程为: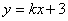 ,代入椭圆方程,消去 ,代入椭圆方程,消去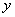 得 得
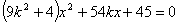 (*) (*)
则 , ,
令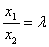 ,则, ,则,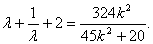
在(*)中,由判别式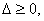 可得 可得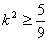 ,从而有 ,从而有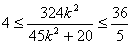 , ,
所以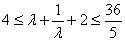 ,解得 ,解得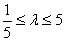 . .
结合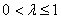 得 得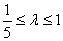 . .
综上,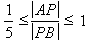 . .
点评:
范围问题不等关系的建立途径多多,诸如判别式法,均值不等式法,变量的有界性法,函数的性质法,数形结合法等等.本题也可从数形结合的角度入手,给出又一优美解法.
例10、在直角坐标平面中,过点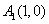 作函数 作函数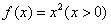 的切线 的切线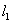 ,其切点为 ,其切点为 ;过点 ;过点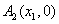 作函数 作函数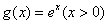 的切线 的切线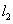 ,其切点为 ,其切点为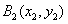 ;过点 ;过点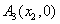 作函数 作函数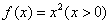 的切线 的切线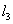 ,其切点为 ,其切点为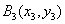 ;如此下去,即过点 ;如此下去,即过点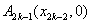 作函数 作函数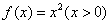 的切线 的切线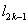 ,其切点为 ,其切点为 ;过点 ;过点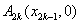 作函数 作函数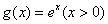 的切线 的切线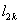 ,其切点为 ,其切点为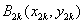 …. ….
(1)探索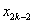 与 与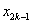 , ,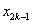 与 与 的关系,说明你的理由,并求 的关系,说明你的理由,并求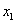 , ,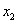 的值; 的值;
(2)求数列 通项公式 通项公式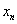 ; ;
(3)是否存在正实数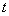 ,使得对于任意的自然数 ,使得对于任意的自然数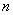 ,不等式 ,不等式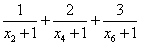 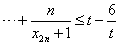 恒成立?若存在,求出这样的实数 恒成立?若存在,求出这样的实数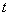 的取值范围;若不存在,则说明理由. 的取值范围;若不存在,则说明理由.
分析:
利用导数先找出切线方程,从而可以确定数列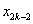 与 与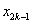 , ,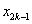 与 与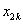 的关系,再分奇数项与偶数项来求出数列的通项,在第三问中可用错位相消法求出不等式左端的和,再证明其单调性来求解. 的关系,再分奇数项与偶数项来求出数列的通项,在第三问中可用错位相消法求出不等式左端的和,再证明其单调性来求解.
解:
(1)∵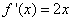 ,∴切线 ,∴切线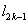 的方程为 的方程为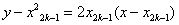 , ,
又切线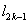 过点 过点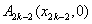 ,∴ ,∴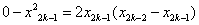 ,且 ,且 ,∴ ,∴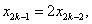 ∴ ∴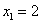 . .
又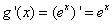 ,∴切线 ,∴切线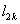 的方程为 的方程为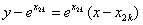 , ,
而切线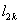 过点 过点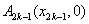 ,∴ ,∴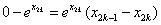 , ,
且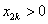 ,∴ ,∴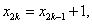 ∴ ∴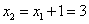 . .
(2)由(1) 可知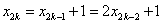 ,即 ,即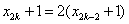 , ,
∴数列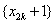 为等比数列,且首项为4, 为等比数列,且首项为4,
∴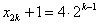 ,即 ,即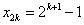 . .
而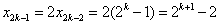 , ,
故数列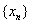 通项公式为 通项公式为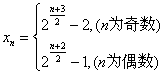
(3)令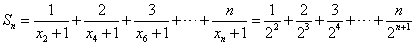
∴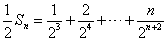 , ,
两式相减得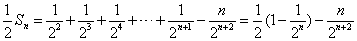
∴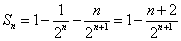 . .
∴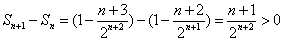 , ,
∴数列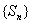 递增. 递增.
又当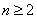 时, 时,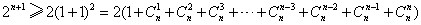
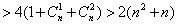 . .
∴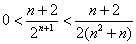 ,而 ,而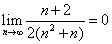 , ,
∴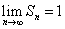 . .
∴对于任意的正整数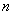 和任意的实数 和任意的实数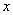 不等式恒成立等价于 不等式恒成立等价于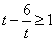 , ,
而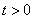 ,所以有 ,所以有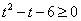 ,解得 ,解得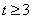 或 或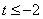 (舍). (舍).
故存在这样的正实数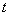 ,其取值范围为 ,其取值范围为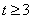 . .
- 返回 -
|