题型一 根据等式的特点,构建方程
例1.设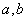 是方程
是方程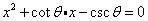 的两个不等实根,那么过点
的两个不等实根,那么过点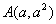 和
和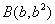 的直线与圆
的直线与圆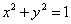 的位置关系是( )
的位置关系是( )
A.相离 B.相切
C.相交 D.随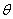 的值而变化
的值而变化
分析:
判断直线与圆的位置关系,即判断圆心到直线的距离与圆的半径的关系.
解:
由题意,得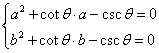 ,即
,即 ,
,
因此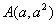 和
和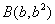 都在直线
都在直线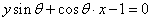 上,∴原点到该直线的距离
上,∴原点到该直线的距离 ,∴过
,∴过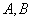 的直线与单位圆相切.
的直线与单位圆相切.
点评:
本题的关键之处在于求出过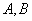 两点的直线方程,这里是从方程的形式中观察出的,灵活运用函数与方程的思想,通过“设而不求”而得出的.
两点的直线方程,这里是从方程的形式中观察出的,灵活运用函数与方程的思想,通过“设而不求”而得出的.
例2.对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知函数f(x)=ax2+(b+1)x+(b-1)(a≠0).
(1)若a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B关于直线y=kx+ 对称,求b的最小值.
对称,求b的最小值.
解:
(1)当a=1,b=-2时,f(x)=x2-x-3,
由题意可知x=x2-x-3,得x1=-1,x2=3.
故当a=1,b=-2时,f(x)的两个不动点为-1,3.
(2)∵f(x)=ax2+(b+1)x+(b-1)(a≠0)恒有两个不动点,
∴x=ax2+(b+1)x+(b-1),
即ax2+bx+(b-1)=0恒有两相异实根.
∴Δ=b2-4ab+4a>0(b∈R)恒成立.
于是Δ′=(4a)2-16a<0解得0<a<1.
故当b∈R,f(x)恒有两个相异的不动点时,0<a<1.
(3)由题意A、B两点应在直线y=x上,设A(x1,x1),B(x2,x2).
又∵A、B关于y=kx+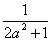 对称.
对称.
∴k=-1. 设AB的中点为M(x′,y′).
∵x1,x2是方程ax2+bx+(b-1)=0的两个根.
∴x′=y′= ,
,
又点M在直线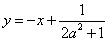 上有
上有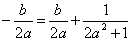 ,
,
即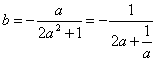 .
.
∵a>0,∴2a+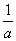 ≥2
≥2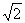 当且仅当2a=
当且仅当2a=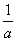 即a=
即a=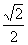 ∈(0,1)时取等号,
∈(0,1)时取等号,
故b≥-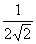 ,得b的最小值-
,得b的最小值-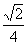 .
.
例3.对于定义域为D的函数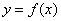 ,若同时满足下列条件:
,若同时满足下列条件:
①f(x)在D内单调递增或单调递减;
②存在区间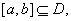 使f(x)在
使f(x)在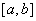 上的值域为
上的值域为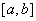 ;那么把
;那么把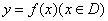 叫闭函数.
叫闭函数.
(1)求闭函数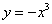 符合条件②的区间
符合条件②的区间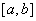 ;
;
(2)判断函数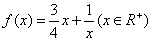 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若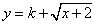 是闭函数,求实数k的范围.
是闭函数,求实数k的范围.
分析:
这是一个新定义型的题目,要能从题中所给信息,进行加工提炼,得出解题的条件.
解:
(1)由题意,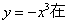
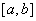 上递减,则
上递减,则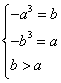 解得
解得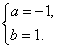
所以,所求的区间为[-1,1].
(2)当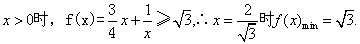
所以,函数在定义域上不单调递增或单调递减,从而该函数不是闭函数.
(3)若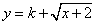 是闭函数,则存在区间[a,b],在区间[a,b]上,函数f(x)的值域为[a,b],即
是闭函数,则存在区间[a,b],在区间[a,b]上,函数f(x)的值域为[a,b],即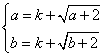 ,
, 的两个实数根,
的两个实数根,
即方程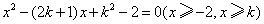 有两个不等的实根.设f(x)=x2-(2k+1)x+k2-2.
有两个不等的实根.设f(x)=x2-(2k+1)x+k2-2.
法一:当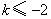 时有
时有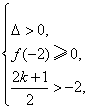 解得
解得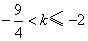 .当
.当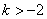 有
有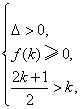 此时不等式组无解.综上所述,
此时不等式组无解.综上所述,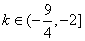 .
.
法二:只需满足方程x2-(2k+1)x+k2-2=0有两大于或等于k的不等实根,即:
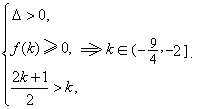
点评:
在解数学题的过程中,寻找一个命题A的等价命题B往往是解题的关键,本题就是运用函数与方程的思想把一个看似函数性质讨论的问题转化为方程解的讨论问题.
题型二 函数与方程思想在数列中的应用
例4.已知等差数列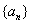 的公差
的公差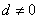 ,对任意
,对任意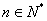 都有
都有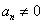 ,函数
,函数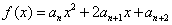 .
.
(1)求证:对任意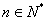 ,函数
,函数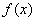 的图象过一定点.
的图象过一定点.
(2)若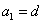 ,函数f(x)与x轴的一个交点为
,函数f(x)与x轴的一个交点为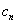 (
( ),且
),且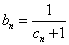 ,求数列
,求数列 的通项公式.
的通项公式.
(3)在(2)的条件下,求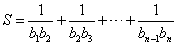 .
.
分析:
函数f(x)的图象过一定点,可运用等差数列的性质进行论证;后一问中可运用根与系数的特点进行求解.
解:
(1)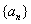 为等差数列,故
为等差数列,故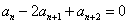 ,故
,故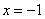 必是方程
必是方程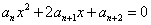 的一个根,即方程
的一个根,即方程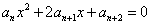 均有一个相同的根为-1.
均有一个相同的根为-1.
故函数f(x)过一定点(-1,0).
(2)方程 的两根为
的两根为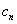 与
与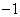 .
.
有 ,故
,故 ,
,
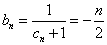 .
.
(3)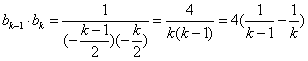 ,
,
故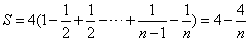 .
.
点评:
数列综合题往往和函数、方程、不等式相结合,以数列为载体,利用函数性质研究数列与方程,或以数列为载体,利用方程为工具去研究相关函数或数列的性质.
题型三 函数与方程思想在不等式中的应用
例5.设a>b>c,且a+b+c=0,抛物线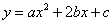 被x轴截得的弦长为l,求证:
被x轴截得的弦长为l,求证: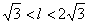 .
.
分析:
由于弦长l是与a,b,c有关的变量,若能建立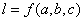 的表达式,那么结论相当于确定该函数的值域.为了确定函数
的表达式,那么结论相当于确定该函数的值域.为了确定函数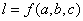 的值域,需要解决好三个问题:一是求出变量l关于a,b,c的解析式;二是将这个多元函数通过集中变量、消元或变量代换转化为一元函数;三是需要确定这个一元函数的定义域.
的值域,需要解决好三个问题:一是求出变量l关于a,b,c的解析式;二是将这个多元函数通过集中变量、消元或变量代换转化为一元函数;三是需要确定这个一元函数的定义域.
证明:
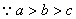 ,且
,且 .从而
.从而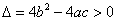 .
.
故抛物线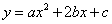 与x轴有两个不同的交点,即方程
与x轴有两个不同的交点,即方程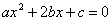 必有两个不相等的实数根
必有两个不相等的实数根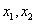 ,由韦达定理得
,由韦达定理得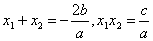 .
.
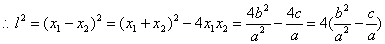
 .
.
可见,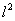 是
是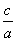 的二次函数.
的二次函数.
由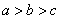 及
及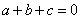 ,得
,得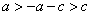 ,解得
,解得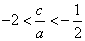 .
.
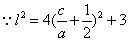 在
在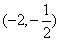 上是减函数,
上是减函数,
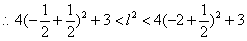 ,
,
即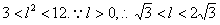 .
.
点评:
应用函数与方程思想处理不等式问题,关键在于构造一个适当的函数和用好方程理论,弄清函数、方程及不等式的内在联系,树立相互转化的观点.
例6.已知函数f(x)=6x-6x2,设函数g1(x)=f(x), g2(x)=f[g1(x)], g3(x)=f[g2(x)],…gn(x)=f[gn-1(x)],…
(1)求证:如果存在一个实数x0,满足g1(x0)=x0,那么对一切n∈N,gn(x0)=x0都成立;
(2)若实数x0满足gn(x0)=x0,则称x0为稳定不动点,试求出所有这些稳定不动点;
(3)设区间A=(-∞,0),对于任意x∈A,有g1(x)=f(x)=a<0,g2(x)=f[g1(x)]=f(0)<0,且n≥2时,gn(x)<0.试问是否存在区间B(A∩B≠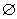 ),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
(1)证明:当n=1时,g1(x0)=x0显然成立;
设n=k时,有gk(x0)=x0(k∈N)成立,
则gk+1(x0)=f[gk(x0)]=f(x0)=g1(x0)=x0.
即n=k+1时,命题成立.
∴对一切n∈N,若g1(x0)=x0,则gn(x0)=x0.
(2)解:由(1)知,稳定不动点x0只需满足f(x0)=x0.
由f(x0)=x0,得6x0-6x02=x0,∴x0=0或x0=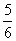 .
.
∴稳定不动点为0和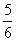 .
.
(3)解:∵f(x)<0,得6x-6x2<0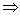 x<0或x>1.
x<0或x>1.
∴gn(x)<0 f[gn-1(x)]<0
f[gn-1(x)]<0 gn-1(x)<0或gn-1(x)>1.
gn-1(x)<0或gn-1(x)>1.
要使一切n∈N,n≥2,都有gn(x)<0,必须有g1(x)<0或g1(x)>1.
由g1(x)<0 6x-6x2<0
6x-6x2<0 x<0或x>1.
x<0或x>1.
由g1(x)>0 6x-6x2>1
6x-6x2>1
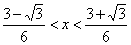 .
.
故对于区间(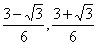 )和(1,+∞)内的任意实数x,
)和(1,+∞)内的任意实数x,
只要n≥2,n∈N,都有gn(x)<0.
题型四 函数与方程思想在三角函数中的应用
例7.已知函数f(x)=x2-(m+1)x+m(m∈R).
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角.求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
分析:
利用一元二次方程的韦达定理、二次函数在区间上的最值的求法,三角函数的值域进行求解.解题时要深挖题意,做到题意条件都明确,隐性条件注意列.列式要周到,不遗漏.
(1)证明:f(x)+4=0即x2-(m+1)x+m+4=0.依题意:
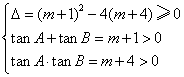 又A、B锐角为三角形内两内角,∴
又A、B锐角为三角形内两内角,∴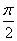 <A+B<π.
<A+B<π.
∴tan(A+B)<0,即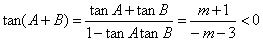 .
.
∴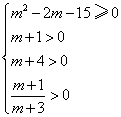 ∴m≥5.
∴m≥5.
(2)证明:∵f(x)=(x-1)(x-m),又-1≤cosα≤1,
∴1≤2+cosα≤3,恒有f(2+cosα)≤0.
即1≤x≤3时,恒有f(x)≤0即(x-1)(x-m)≤0,∴m≥x但xmax=3,∴m≥xmax=3.
(3)解:∵f(sinα)=sin2α-(m+1)sinα+m=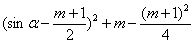 ,
,
且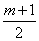 ≥2,∴当sinα=-1时,f(sinα)有最大值8.
≥2,∴当sinα=-1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3.
点评:
在解答过程中,第(1)问中易漏掉Δ≥0和tan(A+B)<0,第(2)问中如何保证f(x)在[1,3]上恒小于等于零为关键.
题型五 函数与方程思想在解析几何中的应用
例8.给定抛物线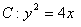 ,F是C的焦点,过点F的直线l与C相交于A,B两点.
,F是C的焦点,过点F的直线l与C相交于A,B两点.
(1)设l的斜率为1,求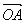 与
与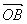 的夹角的大小;
的夹角的大小;
(2)设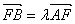 ,若
,若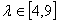 ,求l在y轴上的截距的变化范围.
,求l在y轴上的截距的变化范围.
解:
(1)C的焦点为F(1,0),直线l的斜率为1,
所以l的方程为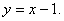 将
将 代入方程
代入方程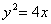 ,并整理得
,并整理得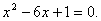
设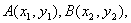 则有
则有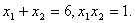
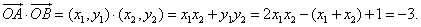
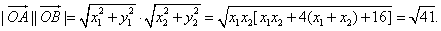
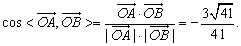
所以 夹角的大小为
夹角的大小为
(2)由题设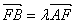 得
得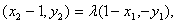
即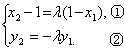
由②得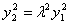 ,∵
,∵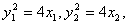 ∴
∴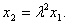 ③
③
联立①、③解得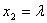 ,依题意有
,依题意有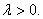 ∴
∴ 又F(1,0),
又F(1,0),
得直线l方程为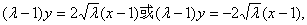
当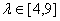 时,l在y轴上的截距为
时,l在y轴上的截距为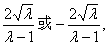
设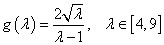 ,
,
可知 在[4,9]上是递减的,(或用导数
在[4,9]上是递减的,(或用导数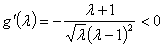 ,证明
,证明 是减函数.)∴
是减函数.)∴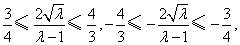
直线l在y轴上截距的变化范围为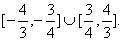
点评:
不少解析几何问题,其中某些元素处于运动变化之中,存在着相互联系、相互制约的量,它们之间往往构成函数关系;对于直线和曲线交点问题,经常要转化为方程问题,用方程的理论加以解决.
例9.直线 和双曲线
和双曲线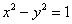 的左支交于A、B两点,直线l过点P(-2,0)和线段AB的中点M,求l在y轴上的截距b的取值范围.
的左支交于A、B两点,直线l过点P(-2,0)和线段AB的中点M,求l在y轴上的截距b的取值范围.
分析:
b的变化是由于k的变化而引起的,即对于k的任一确定的值,b有确定的值与之对应,因此b是k的函数,本题即为求这个函数的值域.
解:由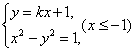 消去y,得
消去y,得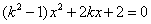 .(
.(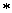 )
)
因为直线m与双曲线的左支有两个交点,所以方程(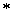 )有两个不相等的负实数根.
)有两个不相等的负实数根.
所以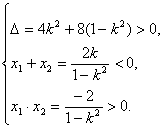 解得
解得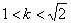 .
.
设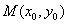 ,则
,则
由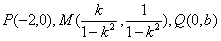 三点共线,得出
三点共线,得出 .
.
设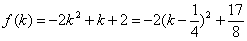 ,则
,则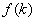 在
在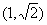 上为减函数,
上为减函数,
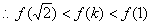 ,且
,且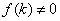 .
.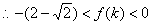 ,或
,或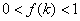 ,
,
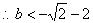 ,或
,或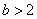 .
.
点评:
根据函数的思想建立b与k的函数关系,根据方程的思想,运用二次方程的理论具体求出b的表达式,是解此题的两个关键问题.不少解析几何问题,其中某些元素处于运动变化之中,存在着相互联系、相互制约的量,它们之间往往构成函数关系;对于直线和曲线交点问题,经常要转化为方程问题,用方程的理论加以解决.
题型六 函数与方程思想在立体几何中的应用
例10.如图,已知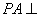 面
面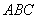 ,
,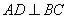 于D,
于D, .
.