极限的概念及其渗透的思想在数学中占有重要的地位,它是人们研究许多问题的工具.
1、有限个函数的和(或积)的极限等于这些函数极限的和(或积),在求几个函数的和(或积)的极限时,一般要化简,再求极限.
2、两个(或几个)函数的极限至少有一个不存在时,他们的和、差、积、商的极限不一定不存在.
3、对
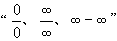 型的极限,要分别通过“约去使分母为零的因式、同除以分子、分母的最高次幂、有理化分子”等变形,化归转化后再求极限值.
型的极限,要分别通过“约去使分母为零的因式、同除以分子、分母的最高次幂、有理化分子”等变形,化归转化后再求极限值.
4、求函数的极限的几种基本的方法:
①代入法;②约去分母为零的因式;③分子、分母同除x的最高次幂;④有理化法
5、函数f(x)在点x0处连续必须具备以下三个条件:
函数f(x)在点x=x0处有定义;
函数f(x)在点x=x0处有极限;
函数f(x)在点x=x0处的极限值等于在这一点x0处的函数值,即 f(x)=f(x0).
f(x)=f(x0).
导数是微积分的初步知识,是研究函数,解决实际问题的有力工具.在高中阶段对于导数的学习,主要是以下几个方面:
1、导数的常规问题:
(1)刻画函数(比初等方法精确细微);
(2)同几何中切线联系(导数方法可用于研究平面曲线的切线);
(3)应用问题(初等方法往往技巧性要求较高,而导数方法显得简便)等关于n次多项式的导数问题属于较难类型.
2、关于函数特征,最值问题较多,所以有必要专项讨论,导数法求最值要比初等方法快捷简便.
3、导数与解析几何或函数图象的混合问题是一种重要类型,也是高考中考察综合能力的一个方向,应引起注意.
4、求复合函数的导数,一般按以下三个步骤进行:
(1)适当选定中间变量,正确分解复合关系;
(2)分步求导(弄清每一步求导是哪个变量对哪个变量求导);
(3)把中间变量代回原自变量(一般是x)的函数.
也就是说,首先选定中间变量,分解复合关系,说明函数关系y=f(μ),μ=f(x);然后将已知函数对中间变量求导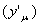 ,中间变量对自变量求导
,中间变量对自变量求导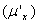 ;最后求
;最后求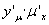 ,并将中间变量代回为自变量的函数.整个过程可简记为分解——求导——回代.熟练以后,可以省略中间过程.若遇多重复合,可以相应地多次用中间变量.
,并将中间变量代回为自变量的函数.整个过程可简记为分解——求导——回代.熟练以后,可以省略中间过程.若遇多重复合,可以相应地多次用中间变量.
例1、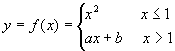 在
在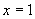 处可导,则
处可导,则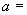 ________,
________,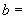 ________.
________.
解:
函数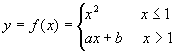 在
在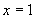 处可导,则必连续,
处可导,则必连续,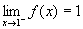 ,
, 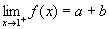 ,
,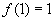 ,∴
,∴ 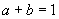 .
.
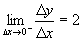 ,
,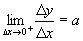 ,∴
,∴ 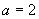 ,
,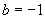 .
.
例2、(08福建)已知函数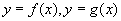 的导函数的图象如下图,那么
的导函数的图象如下图,那么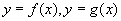 图象可能是( )
图象可能是( )

解:
从导函数的图象可知两个函数在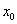 处斜率相同,可以排除B答案,再者导函数的函数值反映的是原函数增加的快慢,可明显看出
处斜率相同,可以排除B答案,再者导函数的函数值反映的是原函数增加的快慢,可明显看出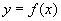 的导函数是减函数,所以原函数应该增加的越来越慢,排除AC,最后就只有答案D了,可以验证y=g(x)的导函数是增函数,增加越来越快.
的导函数是减函数,所以原函数应该增加的越来越慢,排除AC,最后就只有答案D了,可以验证y=g(x)的导函数是增函数,增加越来越快.
答案:D
例3、若数列{an}的首项为a1=1,且对任意n∈N*,an与an+1恰为方程x2-bnx+cn=0的两根,其中0<|c|<1,当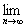 (b1+b2+…+bn)≤3时,求c的取值范围.
(b1+b2+…+bn)≤3时,求c的取值范围.
解:
首先,由题意对任意n∈N*,an·an+1=cn恒成立.
∴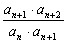 =
=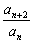 =
=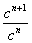 =c.又a1·a2=a2=c.
=c.又a1·a2=a2=c.
∴a1,a3,a5,…,a2n-1,…是首项为1,公比为c的等比数列,a2,a4,a6,…,a2n,…是首项为c,公比为c的等比数列.其次,由于对任意n∈N*,an+an+1=bn恒成立.
∴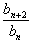 =
=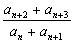 =c.又b1=a1+a2=1+c,b2=a2+a3=2c,
=c.又b1=a1+a2=1+c,b2=a2+a3=2c,
∴b1,b3,b5,…,b2n-1,…是首项为1+c,公比为c的等比数列,b2,b4,b6,…,b2n,…是首项为2c,公比为c的等比数列,
∴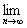 (b1+b2+b3+…+bn)
(b1+b2+b3+…+bn)
= 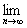 (b1+b3+b5+…)+
(b1+b3+b5+…)+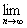 (b2+b4+…)
(b2+b4+…)
=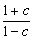 +
+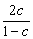 ≤3.
≤3.
解得c≤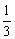 或c>1,∵0<|c|<1,∴0<c≤
或c>1,∵0<|c|<1,∴0<c≤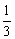 或-1<c<0.
或-1<c<0.
故c的取值范围是(-1,0)∪(0,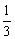 ].
].
例4、(2006浙江)已知函数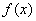 =x3+x2,数列 {xn}(xn>0)的第一项x1=1,以后各项按如下方式取定:曲线y=f(x)在
=x3+x2,数列 {xn}(xn>0)的第一项x1=1,以后各项按如下方式取定:曲线y=f(x)在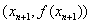 处的切线与经过(0,0)和(xn,f(xn))两点的直线平行(如图).求证:当n
处的切线与经过(0,0)和(xn,f(xn))两点的直线平行(如图).求证:当n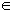
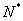 时:
时:
(I)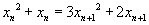 ;(II)
;(II)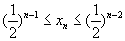
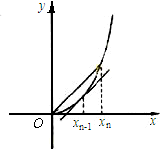
证明:(I)∵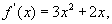
∴曲线 在
在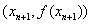 处的切线斜率
处的切线斜率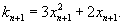
∵过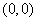 和
和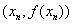 两点的直线斜率是
两点的直线斜率是
∴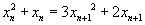 .
.
(II)∵函数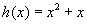 当
当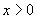 时单调递增,
时单调递增,
而
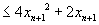
 ,
,
∴ ,即
,即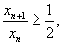
因此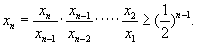
又∵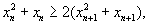
令 则
则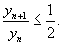
∵ ∴
∴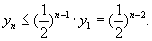
因此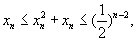 故
故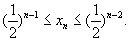
例5、(07山东卷)设函数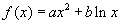 ,其中
,其中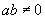 .
.
证明:当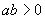 时,函数
时,函数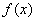 没有极值点;当
没有极值点;当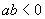 时,函数
时,函数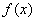 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
证明:
因为 ,所以
,所以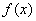 的定义域为
的定义域为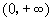 .
.
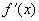
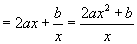 .
.
当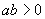 时,如果
时,如果 在
在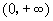 上单调递增;
上单调递增;
如果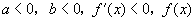 在
在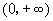 上单调递减.
上单调递减.
所以当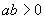 ,函数
,函数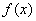 没有极值点.
没有极值点.
当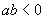 时,
时,
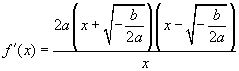
令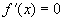 ,得
,得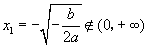 (舍去),
(舍去),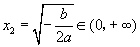 ,
,
当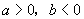 时,
时,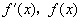 随
随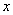 的变化情况如下表:
的变化情况如下表:
从上表可看出,函数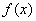 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为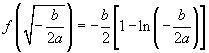 .无极大值.
.无极大值.
当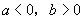 时,
时, 随
随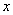 的变化情况如下表:
的变化情况如下表:
从上表可看出,函数 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为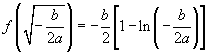 .无极小值.
.无极小值.
综上所述:当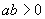 时,函数
时,函数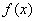 没有极值点;
没有极值点;
当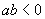 时,
时,
若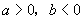 时,函数
时,函数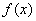 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为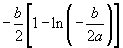 ,无极大值.
,无极大值.
若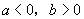 时,函数
时,函数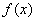 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为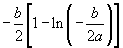 ,无极小值.
,无极小值.
例6、(2006湖北) 设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点.
(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设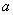 >0,
>0,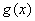 =(
=(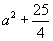 )
)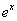 .若存在
.若存在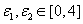 使得|
使得|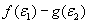 |<1成立,求
|<1成立,求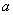 的取值范围.
的取值范围.
解:
(1)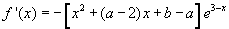 ,
,
由f′(3)=0得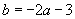 ,
,
所以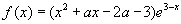
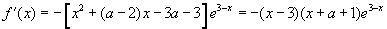 ,
,
令f′(x)=0得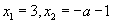 .
.
由于x=3是f(x)的极值点,故x1≠x2,即a≠-4,
当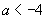 时,
时,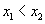 ,故f(x)在
,故f(x)在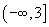 上为减函数,在
上为减函数,在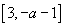 上为增函数,在
上为增函数,在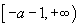 上为减函数.
上为减函数.
当a>-4时,x1>x2,故f (x)在(-∞,-a-1]上为减函数,在[-a-1,3]上为增函数,在[3,+∞)上为减函数.
(2)当a>0时,-a-1<0,故f(x)在[0,3]上为增函数,在[3,+∞)上为减函数.
因此f(x)在[0,4]上的值域为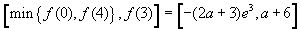 ,
,
而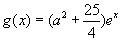 在[0,4]上为增函数,所以值域为
在[0,4]上为增函数,所以值域为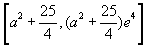 .
.
注意到 ,
,
故由假设知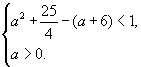 解得
解得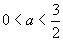 .
.
故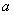 的取值范围是
的取值范围是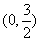 .
.
例7、定义在(0,+∞)上的函数 ,其中e=2.718 28…是自然对数的底数,a∈R.
,其中e=2.718 28…是自然对数的底数,a∈R.
(1)若函数f(x)在点x=1处连续,求a的值;
(2)若函数f(x)为(0,1)上的单调函数,求实数a的取值范围;并判断此时函数f(x)在(0,+∞)上是否为单调函数;
(3)当x∈(0,1)时,记g(x)=lnf(x)+x2-ax. 试证明:对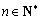 ,当n≥2时,有
,当n≥2时,有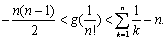
解:
(1)∵f(1)=1,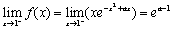 ,
,
已知f(x)在点x=1处连续,∴有ea-1=1. ∴a=1.
(2)当x∈(0,1)时,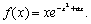
此时,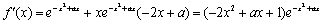 ,
,
∵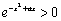 ,
,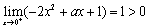 ,∴
,∴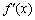 不可能在(0,1)上恒小于0.
不可能在(0,1)上恒小于0.
故f(x)在(0,1)上必为增函数. ∴-2x2+ax+1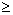 0在(0,1)上恒成立.
0在(0,1)上恒成立.
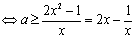 在(0,1)上恒成立.
在(0,1)上恒成立.
设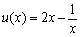 ,x∈(0,1). ∵u(x)在(0,1)上是增函数,u(x)<1.
,x∈(0,1). ∵u(x)在(0,1)上是增函数,u(x)<1.
∴当a≥1时,f(x)在(0,1)上是增函数.
当a=1时,f(x)在(0,+∞)上也是增函数;
当a>1时,∵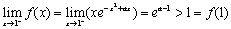 ,
,
此时,f(x)在(0,+∞)上不是增函数.
(3)当x∈(0,1)时,g(x)=lnf(x)+x2-ax=lnx. 当n≥2时,