题型一:排列组合应用题
解决此类问题的方法是:直接法,先考虑特殊元素(或特殊位置),再考虑其他元素(或位置);间接法,所有排法中减去不合要求的排法数;对于复杂的应用题,要合理设计解题步骤,一般是先分组,后分步,要求不重不漏,符合条件.
例1、(08安徽理12)12名同学合影,站成了前排4人后排8人.现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是( )
A.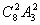 B.
B.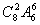 C.
C. D.
D.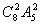
解:
从后排8人中选2人共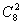 种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,故为
种选法,这2人插入前排4人中且保证前排人的顺序不变,则先从4人中的5个空挡插入一人,有5种插法;余下的一人则要插入前排5人的空挡,有6种插法,故为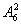 ;综上知选C.
;综上知选C.
例2、(08湖北理6)将5名志愿者分配到3个不同的奥运场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为( )
A.540 B.300 C.180 D.150
解:
将5分成满足题意的3份有1,1,3与2,2,1两种,所以共有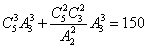 种方案,故D正确.
种方案,故D正确.
例3、四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为( )
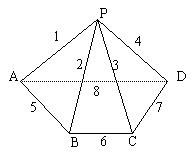
A.96 B.48 C.24 D.0
解:
由题意分析,如图,先把标号为1,2,3,4号化工产品分别放入①②③④4个仓库内共有 种放法;再把标号为5,6,7,8号化工产品对应按要求安全存放:7放入①,8放入②,5放入③,6放入④;或者6放入①,7放入②,8放入③,5放入④;两种放法.综上所述:共有
种放法;再把标号为5,6,7,8号化工产品对应按要求安全存放:7放入①,8放入②,5放入③,6放入④;或者6放入①,7放入②,8放入③,5放入④;两种放法.综上所述:共有 种放法.故选B.
种放法.故选B.
例4、在正方体中,过任意两个顶点的直线中成异面直线的有____________对.
解法一:
连成两条异面直线需要4个点,因此在正方体8个顶点中任取4个点有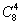 种取法.每4个点可分共面和不共面两种情况,共面的不符合条件得去掉.因为在6个表面和6个体对角面中都有四点共面,故有
种取法.每4个点可分共面和不共面两种情况,共面的不符合条件得去掉.因为在6个表面和6个体对角面中都有四点共面,故有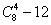 种.但不共面的4点可构成四面体,而每个四面体有3对异面直线,故共有
种.但不共面的4点可构成四面体,而每个四面体有3对异面直线,故共有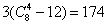 对.
对.
解法二:
一个正方体共有12条棱、12条面对角线、4条体对角线,计28条,任取两条有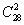 种情况,除去其中共面的情况:(1)6个表面,每个面上有6条线共面,共有
种情况,除去其中共面的情况:(1)6个表面,每个面上有6条线共面,共有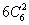 条;(2)6个体对角面,每个面上也有6条线共面,共有
条;(2)6个体对角面,每个面上也有6条线共面,共有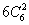 条;(3)从同一顶点出发有3条面对角线,任意两条线都共面,共有
条;(3)从同一顶点出发有3条面对角线,任意两条线都共面,共有 ,故共有异面直线
,故共有异面直线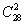 -
-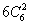 -
- -
-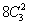 =174对.
=174对.
题型二:求展开式中的系数
例5、(08广东理10)已知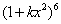 (
(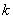 是正整数)的展开式中,
是正整数)的展开式中, 的系数小于120,则
的系数小于120,则 __________.
__________.
解:
 按二项式定理展开的通项为
按二项式定理展开的通项为 ,我们知道
,我们知道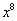 的系数为
的系数为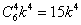 ,即
,即 ,也即
,也即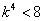 ,而
,而 是正整数,故
是正整数,故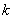 只能取1.
只能取1.
例6、若多项式 ,则a9等于( )
,则a9等于( )
A.9 B.10 C.-9 D.-10
解: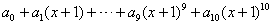
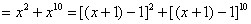
=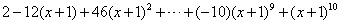
∴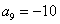 .
.
例7、 展开式中第6项与第7项的系数的绝对值相等,求展开式中系数最大的项和系数绝对值最大的项.
展开式中第6项与第7项的系数的绝对值相等,求展开式中系数最大的项和系数绝对值最大的项.
解:
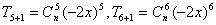 ,依题意有
,依题意有 ,∴n=8.则
,∴n=8.则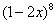 展开式中二项式系数最大的项为
展开式中二项式系数最大的项为 .
.
设第r+1项系数的绝对值最大,则有
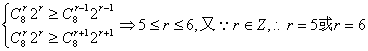 .
.
则系数绝对值最大项为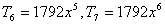 .
.
例8、求证: .
.
证:(法一)倒序相加:设
 ①
①
又∵
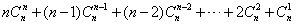 ②
②
∵ ,∴
,∴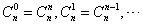 ,
,
由①+②得: ,∴
,∴ ,
,
即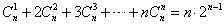 .
.
(法二):左边各组合数的通项为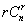
 ,
,
∴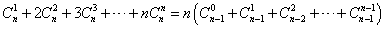
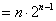 .
.
(法三):

题型三:求复杂事件的概率
例9、(08福建理5)某一批花生种子,如果每1粒发芽的概率为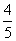 ,那么播下4粒种子恰有2粒发芽的概率是( )
,那么播下4粒种子恰有2粒发芽的概率是( )
A.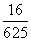 B.
B.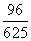 C.
C. D.
D.
解:由 .
.
例10、甲、乙两个围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰,然后负方的队员2号再与对方的获胜队员再赛,负者又被淘汰,一直这样进行下去,直到有一方队员全被淘汰时,另一方获胜,假设每个队员的实力相当,则甲方有4名队员被淘汰,且最后战胜乙方的概率是多少?
解:
根据比赛规则可知,一共比赛了9场,并且最后一场是甲方的5号队员战胜乙方的5号队员,而甲方的前4名队员在前8场比赛中被淘汰,也就是在8次独立重复试验中该事件恰好发生4次的概率,可得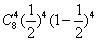 ,又第9场甲方的5号队员战胜乙方的5号队员的概率为
,又第9场甲方的5号队员战胜乙方的5号队员的概率为 ,所以所求的概率为
,所以所求的概率为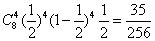 .
.
题型四:求离散型随机变量的分布列、期望和方差
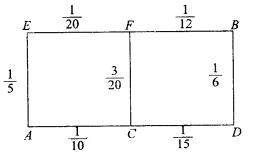
例11、某先生居住在城镇的A处,准备开车到单位B处上班. 若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为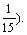
(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求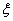 的数学期望
的数学期望
解:
(1)记路段MN发生堵车事件为MN.因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
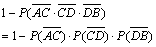
=1-[1-P(AC)][1-P(CD)][1-P(DB)]
=1-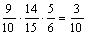 ;
;
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(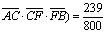 (小于
(小于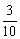 ).
).
路线A→E→F→B中遇到堵车的概率P3为1-P(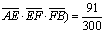 (小于
(小于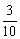 ).
).
显然要使得由A到B的路线途中发生堵车事件的概率最小.只可能在以上三条路线中选择.因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小.
(2)路线A→C→F→B中遇到堵车次数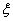 可取值为0,1,2,3.
可取值为0,1,2,3.

答:路线A→C→F→B中遇到堵车次数的数学期望为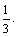
例12、如图所示,甲、乙两只小蚂蚁分别位于一个单位正方体的 点和
点和 点,每只小蚂蚁都可以从每一个顶点处等可能地沿各条棱向各个方向移动,但不能按原线路返回.比如,甲在
点,每只小蚂蚁都可以从每一个顶点处等可能地沿各条棱向各个方向移动,但不能按原线路返回.比如,甲在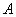 处时可以沿
处时可以沿 、
、 、
、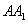 三个方向移动,概率都是
三个方向移动,概率都是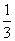 ;到达
;到达 点时,可能沿
点时,可能沿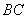 、
、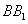 两个方向移动,概率都是
两个方向移动,概率都是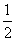 ,已知小蚂蚁每秒钟移动的距离为1个单位.
,已知小蚂蚁每秒钟移动的距离为1个单位.
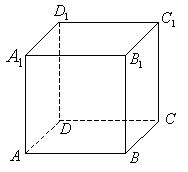
(Ⅰ)若甲、乙两只小蚂蚁都移动1秒钟,则它们所走的路线是异面直线的概率是多少?它们之间的距离为 的概率是多少?
的概率是多少?
(Ⅱ)若乙蚂蚁不动,甲蚂蚁移动3秒钟后,甲、乙两只小蚂蚁之间的距离的期望值是多少?
解:
(Ⅰ)甲蚂蚁移动1秒可以有三种的走法:即沿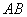 、
、 、
、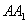 三个方向,当沿
三个方向,当沿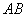 方向时,要使所走的路线成异面直线,乙蚂蚁只能沿
方向时,要使所走的路线成异面直线,乙蚂蚁只能沿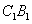 、C1C方向走,概率为
、C1C方向走,概率为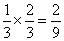 ,同理当甲蚂蚁沿
,同理当甲蚂蚁沿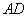 方向走时,乙蚂蚁走
方向走时,乙蚂蚁走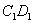 、C1C,概率为
、C1C,概率为 ,甲蚂蚁沿
,甲蚂蚁沿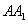 时,乙蚂蚁走
时,乙蚂蚁走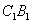 、
、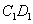 ,概率为
,概率为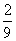 ,因此他们所走路线为异面直线的概率为
,因此他们所走路线为异面直线的概率为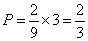 ;
;
甲蚂蚁移动1秒可以有三种走法:即沿 、
、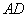 、
、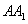 三个方向,当甲沿
三个方向,当甲沿 方向时,要使他们之间的距离为
方向时,要使他们之间的距离为 ,则乙应走
,则乙应走 ,此时的概率为
,此时的概率为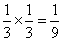 ,同理,甲蚂蚁沿
,同理,甲蚂蚁沿 方向走时、甲蚂蚁沿
方向走时、甲蚂蚁沿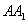 方向走时,概率都为
方向走时,概率都为 ,所以距离为
,所以距离为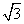 的概率为
的概率为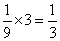 .
.
(Ⅱ)若乙蚂蚁不动,甲蚂蚁移动3秒后,甲乙两个蚂蚁之间距离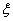 的取值有且只有两个:
的取值有且只有两个: 和
和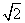 ,当
,当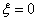 时,甲是按以下路线中的一个走的:
时,甲是按以下路线中的一个走的: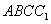 、
、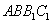 、
、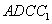 、
、 、
、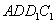 、
、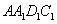 ,所以其概率为
,所以其概率为 ,当
,当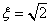 时,甲是按以下路线中的一个走的:
时,甲是按以下路线中的一个走的: 、
、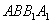 、
、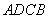 、
、 、
、 、
、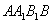 、
、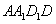 所以其概率为
所以其概率为 ,所以三秒后距离期望值为
,所以三秒后距离期望值为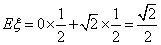 .
.
例13、(08湖北理17)袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球.ξ表示所取球的标号.
(Ⅰ)求ξ的分布列,期望和方差;
(Ⅱ)若η=aξ-b,Eη=1,Dη=11,试求a,b的值.
解:(1)的分布列为:
所以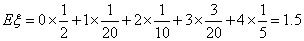 .
.

(2)由 ,得
,得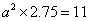 ,即
,即 ,又
,又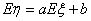 ,所以当
,所以当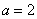 时,由
时,由 ,得
,得 ;当
;当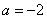 时,由
时,由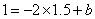 ,得
,得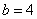 .
.
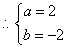 ,或
,或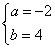 ,即为所求.
,即为所求.
题型五:统计知识
例14、(08广东)某校共有学生2000名,各年级男、女生人数如下表.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
| |
一年级 |
二年级 |
三年级 |
女生 |
373 |
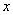
|
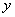
|
男生 |
377 |
370 |

|
A.24 B.18 C.16 D.12
解:
依题意我们知道二年级的女生有380人,那么三年级的学生的人数应该是500,即总体中各个年级的人数比例为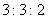 ,故在分层抽样中应在三年级抽取的学生人数为
,故在分层抽样中应在三年级抽取的学生人数为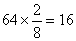 .
.
答案:C
例15、在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布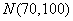 .已知成绩在90分以上(含90分)的学生有12名.
.已知成绩在90分以上(含90分)的学生有12名.
(Ⅰ)试问此次参赛学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?可共查阅的(部分)标准正态分布表 .
.

|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1.2
1.3
1.4
1.9
2.0
2.1 |
0.8849
0.9032
0.9192
0.9713
0.9772
0.9821 |
0.8869
0.9049
0.9207
0.9719
0.9778
0.9826 |
0.888
0.9066
0.9222
0.9726
0.9783
0.9830 |
0.8907
0.9082
0.9236
0.9732
0.9788
0. 9834 |
0.8925
0.9099
0.9251
0.9738
0.9793
0.9838 |
0.8944
0.9115
0.9265
0.9744
0.9798
0.9842 |
0.8962
0.9131
0.9278
0.9750
0.9803
0.9846 |
0.8980
0.9147
0.9292
0.9756
0.9808
0.9850 |
0.8997
0.9162
0.9306
0.9762
0.9812
0.9854 |
0.9015
0.9177
0.9319
0.9767
0.9817
0.9857 |
解:
(Ⅰ)设参赛学生的分数为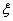 ,因为
,因为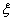 ~N(70,100),由条件知,
~N(70,100),由条件知,
P( ≥90)=1-P(
≥90)=1-P(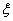 <90)=1-F(90)=1-
<90)=1-F(90)=1-
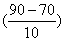
=1-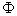 (2)=1-0.9772=0.0228.
(2)=1-0.9772=0.0228.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,因此,参赛总人数约为 ≈526(人).
≈526(人).
(Ⅱ)假定设奖的分数线为x分,则
P(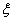 ≥x)=1-P(
≥x)=1-P( <x)=1-F(90)=1-
<x)=1-F(90)=1-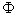
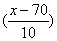 =
= =0.0951,
=0.0951,
即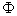
 =0.9049,查表得
=0.9049,查表得 ≈1.31,解得x=83.1.
≈1.31,解得x=83.1.
故设奖的分数线约为83.1分.