题型一:向量的有关概念与运算
此类题经常出现在选择题与填空题中,在复习中要充分理解平面向量的相关概念,熟练掌握向量的坐标运算、数量积运算,掌握两向量共线、垂直的充要条件.
例1、(2007年全国高考II)在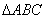 中,已知D是AB边上一点,若
中,已知D是AB边上一点,若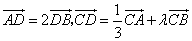 ,则
,则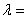 ( )
( )
A.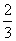 B.
B.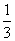 C.
C.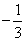 D.
D.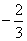
解:
在△ABC中,已知D是AB边上一点,若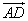 =2
=2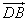 ,
, =
= ,则
,则
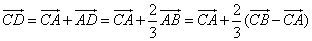 =
=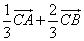 ,
,
∴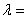
 ,选A.
,选A.
例2.(2007年湖南高考)设 是非零向量,若函数
是非零向量,若函数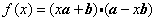 的图象是一条直线,则必有( )
的图象是一条直线,则必有( )
A.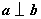 B.
B.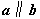
C.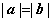 D.
D.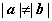
解:
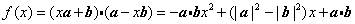 ,若函数
,若函数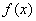 的图象是一条直线,即其二次项系数为0,
的图象是一条直线,即其二次项系数为0,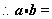 0
0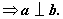 选A.
选A.
例3.已知| a |=1,| b |=1,a与b的夹角为60°,x =2a-b,y=3b-a,则x与y的夹角是多少?
解:
由已知|a|=|b|=1,a与b的夹角α为60°,得a·b=|a||b|cosα=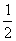 .
.
要计算x与y的夹角θ,需求出|x|,|y|,x·y的值.
∵|x|2=x2=(2a-b)2=4a2-4a·b+b2=4-4× +1=3,
+1=3,
|y|2=y2=(3b-a)2=9b2-6b·a+a2=9-6×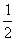 +1=7.
+1=7.
x·y=(2a-b)·(3b-a)=6a·b-2a2-3b2+a·b
=7a·b-2a2-3b2 =7× -2-3=-
-2-3=-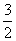 ,
,
又∵x·y=|x||y|cosθ,即-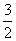 =
=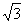 ×
×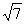 cosθ,
cosθ,
∴cosθ=- ,θ=π-arccos
,θ=π-arccos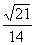 .
.
即x与y的夹角是π-arccos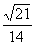 .
.
点评:
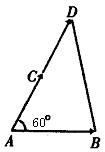
①本题利用模的性质|a|2=a2,②在计算x,y的模时,还可以借助向量加法、减法的几何意义获得,如图所示,设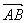 =b,
=b,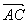 =a,
=a,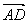 =2a,∠BAC=60°.由向量减法的几何意义,得
=2a,∠BAC=60°.由向量减法的几何意义,得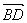 =
= -
- =2a-b.由余弦定理易得|
=2a-b.由余弦定理易得|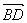 |=
|=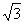 ,即|x|=
,即|x|=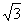 ,同理可得|y|=
,同理可得|y|=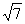 .
.
题型二:平面向量与函数、不等式的综合运用
当平面向量给出的形式中含有未知数时,由向量平行或垂直的充要条件可以得到关于该未知数的关系式.在此基础上,可以设计出有关函数、不等式的综合问题.此类题的解题思路是转化为代数运算,其转化途径主要有两种:①利用向量平行或垂直的充要条件,②利用向量数量积的公式和性质.
例4.已知平面向量a=(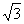 ,-1),b=(
,-1),b=(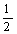 ,
, ).
).
(1) 若存在实数k和t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,试求函数的关系式k=f(t);
(2) 根据(1)的结论,确定k=f(t)的单调区间.
解:
(1)法一:由题意知x=(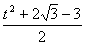 ,
,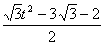 ),
),
y=(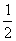 t-
t-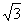 k,
k, t+k),又x⊥y.
t+k),又x⊥y.
故x · y=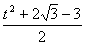 ×(
×( t-
t-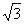 k)+
k)+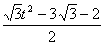 ×(
×( t+k)=0.
t+k)=0.
整理得:t3-3t-4k=0,即k= t3-
t3- t.
t.
法二:∵a=(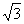 ,-1),b=(
,-1),b=(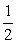 ,
,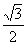 ),∴
),∴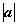 =2,
=2,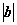 =1且a⊥b.
=1且a⊥b.
∵x⊥y,∴x · y=0,即-k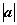 2+t(t2-3)
2+t(t2-3)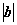 2=0,
2=0,
∴t3-3t-4k=0,即k= t3-
t3- t.
t.
(2) 由(1)知:k=f(t) =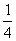 t3-
t3- t,∴kˊ=fˊ(t) =
t,∴kˊ=fˊ(t) =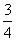 t2-
t2-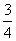 ,
,
令kˊ<0得-1<t<1;令kˊ>0得t<-1或t>1.
故k=f(t)的单调递减区间是(-1,1 ),单调递增区间是(-∞,-1)和(1,+∞).
点评:
第(1)问中两种解法是解决向量垂直的两种常见的方法:一是先利用向量的坐标运算分别求得两个向量的坐标,再利用向量垂直的充要条件;二是直接利用向量垂直的充要条件,其过程要用到向量的数量积公式及求模公式,达到同样的求解目的(但运算过程大大简化,值得注意).第(2)问中求函数的极值运用是求导的方法,这是新旧知识交汇点处的综合运用.
演变:已知平面向量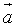 =(
=(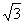 ,-1),
,-1),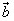 =(
=(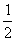 ,
,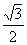 ),若存在不为零的实数k和角α,使向量
),若存在不为零的实数k和角α,使向量 =
=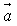 +(sinα-3)
+(sinα-3)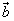 ,
,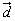 =-k
=-k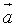 +(sinα)
+(sinα)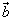 ,且
,且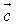 ⊥
⊥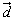 ,试求实数k 的取值范围.
,试求实数k 的取值范围.
解:由条件可得:k=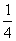 (sinα-
(sinα- )2-
)2- ,而-1≤sinα≤1,
,而-1≤sinα≤1,
∴当sinα=-1时,k取最大值1;sinα=1时,k取最小值-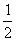 .
.
又∵k≠0,∴k的取值范围为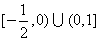 .
.
题型三:平面向量与三角函数的综合运用
向量与三角函数结合,题目新颖而又精巧,既符合在知识的“交汇处”构题,又加强了对双基的考查.
例5.(2007年天津高考)设两个向量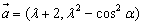 和
和 其中
其中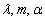 为实数.若
为实数.若 则
则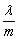 的取值范围是( )
的取值范围是( )
A.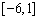 B.
B. C.
C.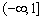 D.
D.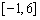
解:
由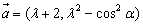



可得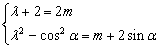 ,
,
设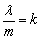 代入方程组可得
代入方程组可得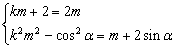
消去 化简得
化简得 ,
,
再化简得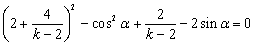 ,
,
再令 代入上式得
代入上式得 ,
,
可得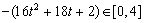 ,解不等式得
,解不等式得 .
.
因而 ,解得
,解得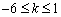 .故选A.
.故选A.
例6.设函数f (x)=a·b,其中向量a=(2cosx,1),b=(cosx,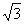 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1- ,且x∈[-
,且x∈[-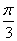 ,
,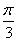 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(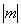 <
<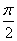 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
思路分析:
本题主要考查平面向量的概念和计算、平移公式以及三角函数的恒等变换等基本技能.
解:
(1)依题设,f(x)=(2cosx,1)·(cosx,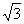 sin2x)
sin2x)
=2cos2x+ sin2x=1+2sin(2x+
sin2x=1+2sin(2x+ ).
).
由1+2sin(2x+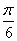 )=1-
)=1-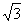 ,得sin(2x+
,得sin(2x+ )=-
)=-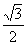 .
.
∵-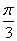 ≤x≤
≤x≤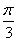 ,∴-
,∴- ≤2x+
≤2x+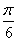 ≤
≤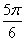 ,
,
∴2x+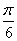 =-
=-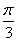 ,即x=-
,即x=-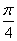 .
.
(2)函数y=2sin2x的图象按向量c=(m ,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(1)得f (x)=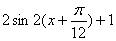 ,∵
,∵ <
<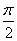 ,∴m=-
,∴m=-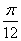 ,n=1.
,n=1.
点评:
①把函数的图像按向量平移,可以看成是C上任一点按向量平移,由这些点平移后的对应点所组成的图象是Cˊ,明确了以上点的平移与整体图象平移间的这种关系,也就找到了此问题的解题途径.②一般地,函数y=f (x)的图象按向量a=(h,k)平移后的函数解析式为y-k=f(x-h).
题型四:平面向量与解析几何的综合运用
由于向量既能体现“形”的直观位置特征,又具有“数”的良好运算性质,是数形结合与转换的桥梁和纽带,因此在向量与解析几何交汇处设计试题,已逐渐成为高考命题的一个新的亮点.平面向量与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,解决此类问题基本思路是将几何问题坐标化、符号化、数量化,从而将推理转化为运算;或者考虑向量运算的几何意义,利用其几何意义解决有关问题.
例7.椭圆的中心是原点O,它的短轴长为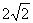 ,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,
,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,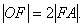 过点A的直线与椭圆相交于P、Q两点.
过点A的直线与椭圆相交于P、Q两点.
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)设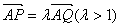 ,过点P且平行于准线l的直线与椭圆相交于另一点M,求证:
,过点P且平行于准线l的直线与椭圆相交于另一点M,求证: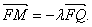
解:
(Ⅰ) 椭圆方程为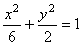 ,离心率
,离心率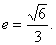
(Ⅱ)证明:设P(x1,y1),Q (x2,y2),又A(3,0),
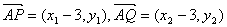 ,
,
由已知得方程组: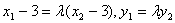 ;
;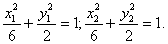
注意λ>1,消去x1、y1和y2得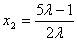 ,因F(2 ,0),M(x1,-y1),
,因F(2 ,0),M(x1,-y1),
故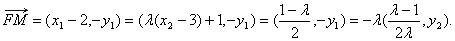
而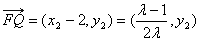 .所以
.所以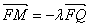 .
.
点评:
运用向量共线的充要条件来处理解几种有关平行、共线等问题思路清晰,易于操作,比用斜率或定比分点公式研究这类问题要简捷的多.
题型五:平面向量与三角形的“心”有关问题
(I)与“重心”有关的向量问题
例8.已知O为平面内一点,A、B、C是平面上不共线的三点,动点P满足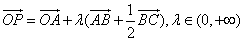 ,则动点P的轨迹一定通过
,则动点P的轨迹一定通过 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
解:
由 得
得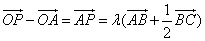 ,取BC的中点D,则
,取BC的中点D,则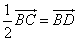 ,故
,故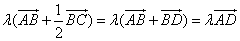 ,所以A、P、D三点共线,故动点P的轨迹一定通过
,所以A、P、D三点共线,故动点P的轨迹一定通过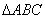 的重心.故选A.
的重心.故选A.
(II)与“垂心”有关的向量问题
例9.已知O为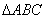 所在平面内一点,满足
所在平面内一点,满足 ,则点O是
,则点O是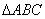 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
解:
设 ,由
,由 可得:
可得: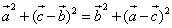 ,即
,即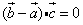 ,∴
,∴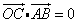 ,故
,故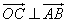 ,同理可得
,同理可得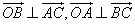 ,∴O是
,∴O是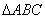 的垂心.故选B.
的垂心.故选B.
例10.已知O是平面上的一定点,A、B、C是平面上不共线的三个点,动点P满足 ,则动点P的轨迹一定通过
,则动点P的轨迹一定通过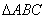
的( )
A.重心 B.垂心 C.外心 D.内心
解:
所给式子可化为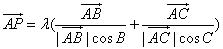 ,
,
由于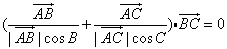 .
.
故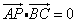 ,∴动点P的轨迹一定通过
,∴动点P的轨迹一定通过 的垂心.故选B.
的垂心.故选B.
(III)与“外心”有关的向量问题
例11.已知O为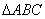 所在平面内一点,若
所在平面内一点,若 ,则O是
,则O是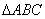 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
解:
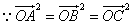 ,∴
,∴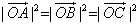 ,即
,即 ,故O是
,故O是 的外心.故选C.
的外心.故选C.
例12.已知O是平面上的一定点,A、B、C是平面上不共线的三个动点,点P满足
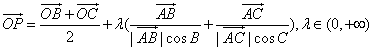 ,则动点P的轨迹一定通过
,则动点P的轨迹一定通过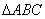 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
解:
设BC的中点为D,则可知当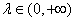 时,
时, 表示垂直于BC的向量,所以点P在BC的垂直平分线上,即动点P的轨迹一定通过
表示垂直于BC的向量,所以点P在BC的垂直平分线上,即动点P的轨迹一定通过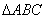 的外心.故选C.
的外心.故选C.
(IV)与“内心”有关的向量问题
例13.已知O为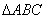 所在平面内一点,A、B、C所对的边分别为a、b、c,若
所在平面内一点,A、B、C所对的边分别为a、b、c,若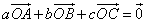 ,则O是
,则O是 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
解:
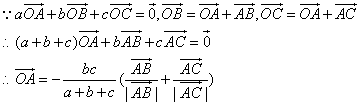
∵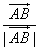 与
与 分别是
分别是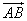 和
和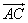 方向上的单位向量,设
方向上的单位向量,设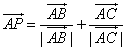 ,可知AP平分
,可知AP平分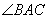 ,所以AO平分
,所以AO平分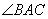 ,同理可证OB平分
,同理可证OB平分 ,OC平分
,OC平分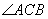 .故应选D.
.故应选D.
专题小结
1、要充分理解平面向量的相关概念,熟练掌握向量的坐标运算、数量积运算,掌握两向量共线、垂直的充要条件.
2、向量与函数、不等式的综合问题,解题思路是转化为代数运算,其转化途径主要有两种:①利用向量平行或垂直的充要条件,②利用向量数量积的公式和性质.
3、平面向量与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,解决此类问题基本思路是将几何问题坐标化、符号化、数量化,从而将推理转化为运算;或者考虑向量运算的几何意义,利用其几何意义解决有关问题.