本章内容是中学数学的重点之一,它既具有相对的独立性,又具有一定的综合性和灵活性,也是初等数学与高等数学的一个重要的衔接点,因而历来是高考的重点.
高考对本章考查比较全面,等差、等比数列,数列的极限的考查几乎每年都不会遗漏.就近五年高考试卷平均计算,本章内容在文史类中分数占13%,理工类卷中分数占11%,由此可以看出数列这一章的重要性.
本章在高考中常见的试题类型及命题趋势:
(1)数列中 与
与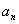 的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意
的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意 与
与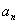 的关系.关于递推公式,在《考试说明》中的考试要求是:“了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项”,近几年命题严格按照《考试说明》,不要求较复杂由递推公式求通项问题.
的关系.关于递推公式,在《考试说明》中的考试要求是:“了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前几项”,近几年命题严格按照《考试说明》,不要求较复杂由递推公式求通项问题.
(2)探索性问题在数列中考查较多,试题没有给出结论,需要考生猜出或自己找出结论,然后给以证明.探索性问题对分析问题解决问题的能力有较高的要求.
(3)等差、等比数列的基本知识必考.这类考题既有选择题,填空题,又有解答题;有容易题、中等题,也有难题.
(4)求和问题也是常见的试题,等差数列、等比数列及可以转化为等差、等比数列求和问题应掌握,还应该掌握一些特殊数列的求和.
(5)将数列应用题转化为等差、等比数列问题也是高考中的重点和热点,从本章在高考中所占的分值来看,一年比一年多,而且多注重能力的考查.
通过上述分析,在学习中应着眼于教材的基本知识和方法,不要盲目扩大,应着重做好以下几方面:
理解概念,熟练运算
巧用性质,灵活自如
考点一:数列的通项与它的前n项和
例1、只能被1和它本身整除的自然数(不包括1)叫做质数.41,43,47,53,61,71,83,97是一个由8个质数组成的数列,小王正确地写出了它的一个通项公式,并根据通项公式得出数列的后几项,发现它们也是质数.试写出一个数P满足小王得出的通项公式,但它不是质数,则P=__________.
解析:
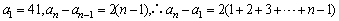 ,
,
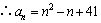 .显然当
.显然当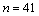 时
时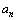 有因数41,此时
有因数41,此时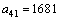 .
.
答案:1681
点评:
本题主要考查了根据数列的前n项写数列的通项的能力.体现了根据数列的前n项写通项只能是满足前n项但不一定满足其所有的性质的特点.
例2、已知等差数列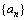 中,
中,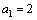 ,前10项之和是15,又记
,前10项之和是15,又记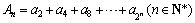 .
.
(1)求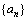 的通项公式;
的通项公式;
(2)求 ;
;
(3)求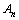 的最大值.(参考数据:ln2=0.6931)
的最大值.(参考数据:ln2=0.6931)
解析:
(1)由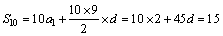 ,得
,得 ,
,
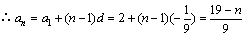 .
.
(2)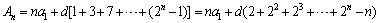
 .
.
(3)法一: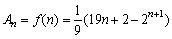 ,
, ,由ln2=0.6931,计算
,由ln2=0.6931,计算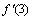 >0,
>0,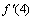 <0,所以极大值点
<0,所以极大值点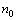 满足
满足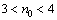 ,但
,但 ,所以只需比较
,所以只需比较 与
与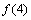 的大小:
的大小: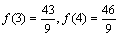 ,
,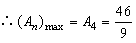 .
.
法二:数列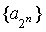 的通项
的通项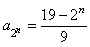 ,
,
令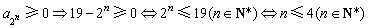 ,
,
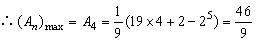 .
.
点评:
求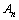 时,也可先求出
时,也可先求出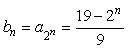 ,这要正确理解“
,这要正确理解“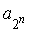 ”,其中
”,其中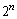 应处在
应处在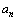 的表达式中
的表达式中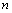 的位置.
的位置.
例3、已知数列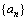 的首项
的首项 ,前
,前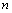 项和为
项和为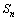 ,且
,且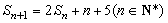 .
.
(1)证明数列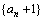 是等比数列;
是等比数列;
(2)令 ,求函数
,求函数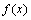 在点
在点 处的导数
处的导数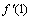 ,并比较
,并比较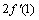 与
与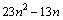 的大小.
的大小.
解析:
(1)由已知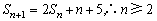 时,
时,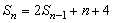 .
.
两式相减,得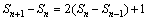 ,即
,即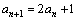 ,从而
,从而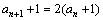 .
.
当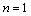 时,
时,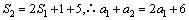 .
.
又 .从而
.从而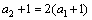 .
.
故总有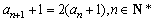 .
.
又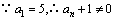 .从而
.从而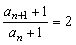 .
.
即 是以
是以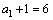 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
(2)由(1)知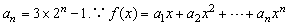 ,
,
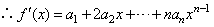 .
.
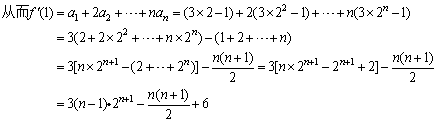
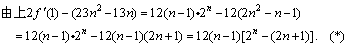
当n=1时,(*)式=0,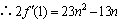 ;
;
当n=2时,(*)式=-12<0,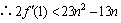 ;
;
当n≥3时,n-1>0.
又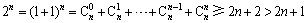 ,
,
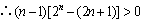 ,即(*)式>0,从而
,即(*)式>0,从而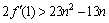 .
.
考点二:等差数列与等比数列
例4、有n2(n≥4)个正数,排成n×n矩阵(n行n列的数表,如下图).

其中每一行的数成等差数列,每一列的数成等比数列,并且所有的公比都相等,且满足:
a24=1,a42=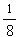 ,a43=
,a43=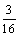 ,
,
(1)求公比q;
(2)用k表示a4k;
(3)求a11+a22+a33+…+ann的值.
分析:
解答本题的关键首先是阅读理解,熟悉矩阵的排列规律,其次是灵活应用等差、等比数列的相关知识求解.
解:
(1)∵每一行的数列成等差数列,
∴a42,a43,a44成等差数列,∴2a43= a42+a44,a44=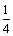 ;
;
又每一列的数成等比数列,a44=a24·q2,a24=1,∴q2=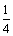 ,且an>0,∴q=
,且an>0,∴q=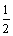 .
.
(2)a4k= a42+(k-2)d=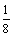 +(k-2)( a43-a42)=
+(k-2)( a43-a42)= .
.
(3)∵第k列的数成等比数列,∴akk= a4k·qk-4=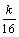 ·(
·(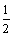 )k-4= k·(
)k-4= k·(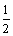 )k (k=1,2,…,n).记a11+a22+a33+…+ann=Sn,则Sn=
)k (k=1,2,…,n).记a11+a22+a33+…+ann=Sn,则Sn=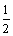 +2·(
+2·(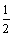 )2+3·(
)2+3·(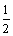 )2+…+n·(
)2+…+n·(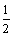 )n,
)n,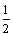 Sn=(
Sn=(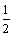 )2+2·(
)2+2·(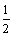 )3+…+(n-1) (
)3+…+(n-1) (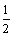 )n+n(
)n+n(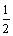 )n+1,
)n+1,
两式相减,得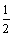 Sn=
Sn=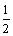 +(
+(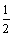 )2+…+(
)2+…+( )n-n(
)n-n(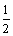 )n+1=1-
)n+1=1-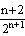 ,
,
∴Sn=2-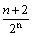 ,即a11+a22+a33+…+ann=2-
,即a11+a22+a33+…+ann=2-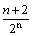 .
.
例5、已知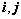 分别是
分别是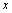 轴,
轴,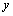 轴方向上的单位向量,
轴方向上的单位向量,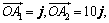 且
且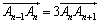 (n=2,3,4,…),在射线
(n=2,3,4,…),在射线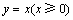 上从下到上依次有点
上从下到上依次有点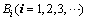 ,
,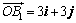 且
且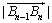 =
=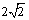 (n=2,3,4,…).
(n=2,3,4,…).
(1)求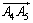 ;
;
(2)求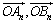 ;
;
(3)求四边形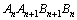 面积的最大值.
面积的最大值.
解析:
(1)由已知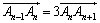 ,得
,得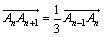 ,
,

(2)由(1)知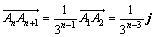 ,
,
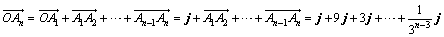
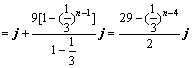 .
.
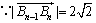 且
且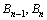 均在射线
均在射线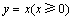 上,
上,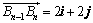 .
.
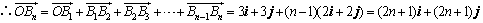 .
.
(3)四边形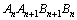 的面积为
的面积为 .
.
又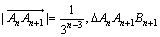 的底边
的底边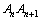 上的高为
上的高为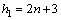 .
.
又 到直线
到直线 的距离为
的距离为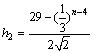 .
.
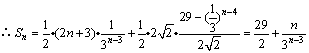 ,
,
而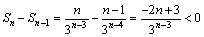 ,
,
 .
.
点评:
本题将向量、解析几何与等差、等比数列有机的结合,体现了在知识交汇点设题的命题原则.其中割补法是解决四边形面积的常用方法.
考点三:数列的极限
例6、给定抛物线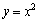 ,过原点作斜率为1的直线交抛物线于点
,过原点作斜率为1的直线交抛物线于点 ,其次过
,其次过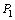 作斜率为
作斜率为 的直线与抛物线交于
的直线与抛物线交于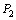 .过
.过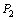 作斜率为
作斜率为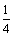 的直线与抛物线交于
的直线与抛物线交于 ,由此方法确定:
,由此方法确定: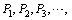 一般地说,过
一般地说,过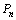 作斜率为
作斜率为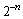 的直线与抛物线交于点
的直线与抛物线交于点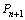 .设
.设 的坐标为
的坐标为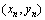 ,试求
,试求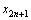 ,再试问:点
,再试问:点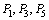 ,…向哪一点无限接近?
,…向哪一点无限接近?
解析:
∵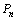 、
、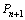 都位于抛物线
都位于抛物线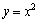 上,从而它们的坐标分别为
上,从而它们的坐标分别为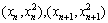 ,∴直线
,∴直线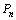
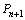 的斜率为
的斜率为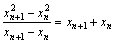 ,于是
,于是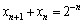 ,
,
即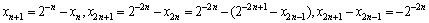 ,
,
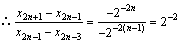 .因此,数列
.因此,数列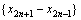 是首项为
是首项为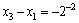 ,
,
公比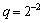 的等比数列.又
的等比数列.又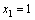 ,
,
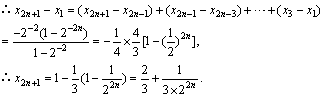
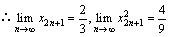 ,因此点列
,因此点列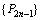 向点
向点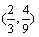 无限接近.
无限接近.
点评:
本例考查极限的计算在几何图形变化中的应用,求解问题的关键是要利用图形的变化发现点运动的规律,从而便于求出极限值来.
例7、已知点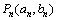 满足:对任意的
满足:对任意的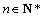 ,
,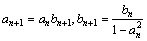 .又已知
.又已知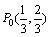 .
.
(1)求过点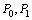 的直线
的直线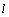 的方程;
的方程;
(2)证明点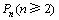 在直线
在直线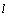 上;
上;
(3)求点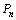 的极限位置.
的极限位置.
解析:
(1) ,
,
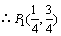 ,则
,则 .
.
化简得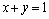 ,即直线
,即直线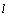 的方程为
的方程为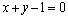 .
.
(2)已知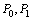 在直线
在直线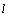 上,假设
上,假设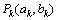 在直线
在直线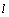 上,则有
上,则有 ,此时
,此时
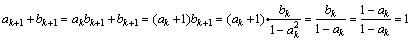 ,
,
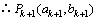 也在直线
也在直线 上.
上.
∴点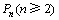 在直线
在直线 上.
上.
(3) ,
,
即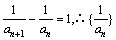 构成等差数列,公差
构成等差数列,公差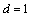 ,首项
,首项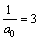 ,
,
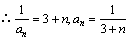 ,故
,故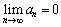 .
.
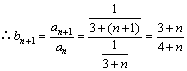 .
.
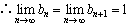 .故
.故 的极限位置为(0,1).
的极限位置为(0,1).
考点四:数学归纳法
例8、设 是满足不等式
是满足不等式 的自然数
的自然数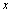 的个数.
的个数.
(1)求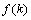 的解析式;
的解析式;
(2)设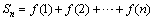 ,求
,求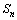 的解析式;
的解析式;
(3) ,试比较
,试比较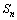 与
与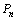 的大小.
的大小.
解析:
先由条件解关于 的不等式,从而求出
的不等式,从而求出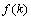 .
.
(1)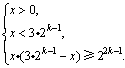 即
即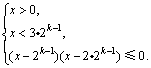
得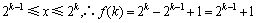 .
.
(2)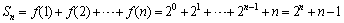 .
.
(3)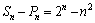 .
.
n=1时,21-12>0;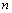 =2时,22-22=0;n=3时,23-32<0;n=4时,24-42=0;n=5时,25-52>0;n=6时,26-62>0.
=2时,22-22=0;n=3时,23-32<0;n=4时,24-42=0;n=5时,25-52>0;n=6时,26-62>0.
猜想:n≥5时,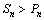 ,下面对n≥5时2n>n2用数学归纳法证明:
,下面对n≥5时2n>n2用数学归纳法证明:
(i)当n=5时,已证25>52.
(ii)假设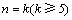 时,
时, ,那么
,那么
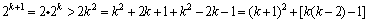 .
.
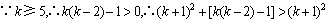 .
.
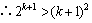 ,即当
,即当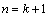 时不等式也成立.
时不等式也成立.
根据(i)和(ii)时,对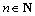 ,n≥5,2n>n2,即
,n≥5,2n>n2,即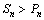 .
.
综上,n=1或n≥5时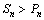 ,n=2或n=4时
,n=2或n=4时 时
时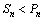 .
.
点评:
这是一道较好的难度不太大的题,它考查了对数、不等式的解法,数列求和及数学归纳法等知识.对培养学生综合分析问题的能力有一定作用.
例9、已知数列 中
中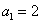 ,
,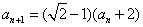 ,
,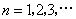 .
.
(1)求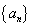 的通项公式;
的通项公式;
(2)若数列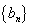 中
中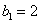 ,
, ,
,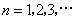 ,
,
证明: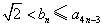 ,
,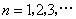 .
.
解:
(1)由题设:
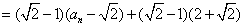
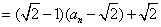 ,
,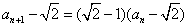 .
.
所以,数列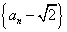 是首项为
是首项为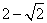 ,公比为
,公比为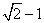 的等比数列,
的等比数列,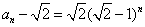 ,
,
即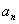 的通项公式为
的通项公式为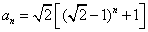 ,
, .
.
(2)用数学归纳法证明.
(ⅰ)当 时,因
时,因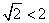 ,
,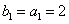 ,所以
,所以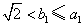 ,结论成立.
,结论成立.
(ⅱ)假设当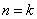 时,结论成立,即
时,结论成立,即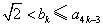 ,也即
,也即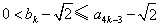 .
.
当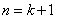 时,
时,
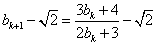
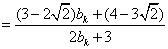
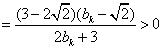 ,
,
又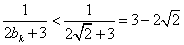 ,
,
所以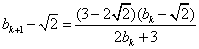


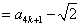 .
.
也就是说,当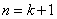 时,结论成立.
时,结论成立.
根据(ⅰ)和(ⅱ)知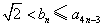 ,
,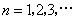 .
.
考点五:数列的应用
例10、李先生因病到医院求医,医生给他开了处方药(片剂),要求每12小时服一片,已知该药片每片220毫克,他的肾脏每12小时排出这种药的60%,并且如果这种药在体内残留量超过386毫克,将会产生副作用,请问:
李先生第一天上午8时第一次服药,则第二天早上8时服完药时,药在他体内的残留量是多少毫克?
如果李先生坚持长期服用此药,会不会产生副作用?为什么?
解:
(1)设第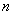 次服药后,药在他体内残留量为
次服药后,药在他体内残留量为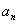 毫克,依题意,
毫克,依题意,
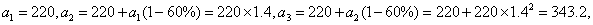
故第二天早上8时第三次服完药时,药在他体内的残留量是343.2毫克.
(2)由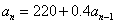 ,
,
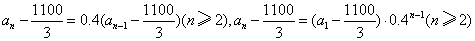 ,
,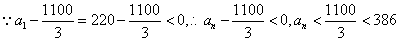 .
.
故长期服用此药不会产生副作用.
例11、(07安徽高考)某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为a1,以后每年交纳的数目均比上一年增加d(d>0),因此,历年所交纳的储务金数目a1,a2,…是一个公差为d的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为r(r>0),那么,在第n年末,第一年所交纳的储备金就变为a1(1+r)n-1,第二年所交纳的储备金就变为a2(1+r)n-2,……,以Tn表示到第n年末所累计的储备金总额。
(1)写出Tn与Tn-1(n≥2)的递推关系式;
(2)求证:Tn=An+Bn,其中{An}是一个等比数列,{Bn}是一个等差数列.
解:
(1)我们有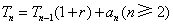 .
.
(2)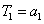 ,对
,对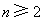 反复使用上述关系式,得
反复使用上述关系式,得

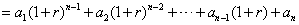 ,①
,①
在①式两端同乘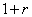 ,得
,得
 ②
②
②-①,得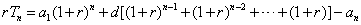
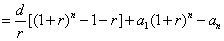 .
.
即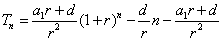 .
.
如果记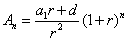 ,
,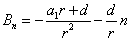 ,则
,则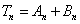 .其中
.其中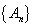 是以
是以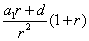 为首项,以
为首项,以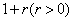 为公比的等比数列;
为公比的等比数列;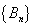 是以
是以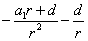 为首项,
为首项,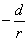 为公差的等差数列.
为公差的等差数列.