高考试题中的三角函数题相对比较传统,难度较低,位置靠前,重点突出.因此,在复习过程中既要注重三角知识的基础性,突出三角函数的图象、周期性、单调性、奇偶性、对称性等性质.以及化简、求值和最值等重点内容的复习,又要注重三角知识的工具性,突出三角与代数、几何、向量的综合联系,以及三角知识的应用意识.
在解题中常用的方法技巧:
1.三角函数恒等变形的基本策略.
(1)常值代换:特别是用“1”的代换,如1=cos2θ+sin2θ=tanθ·cotθ=tan45°等.
(2)项的分拆与角的配凑.如分拆项:sin2θ+2cos2θ=(sin2θ+cos2θ)+cos2θ=1+cos2θ;配凑角:α=(α+β)-β,β=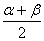 -
-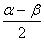 等.
等.
(3)降次与升次.即倍角公式降次与半角公式升次.
(4)化弦(切)法.将三角函数利用同角三角函数基本关系化成弦(切).
(5)引入辅助角.asinθ+bcosθ=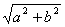 sin(θ+
sin(θ+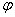 ),这里辅助角
),这里辅助角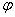 所在象限由a、b的符号确定,
所在象限由a、b的符号确定,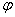 角的值由tan
角的值由tan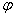 =
=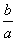 确定.
确定.
(6)万能代换法.巧用万能公式可将三角函数化成tan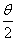 的有理式.
的有理式.
2.证明三角等式的思路和方法.
(1)思路:利用三角公式进行化名,化角,改变运算结构,使等式两边化为同一形式.
(2)证明方法:综合法、分析法、比较法、代换法、相消法、数学归纳法.
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等.
4.解答三角高考题的策略.
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”.
(2)寻找联系:运用相关公式,找出差异之间的内在联系.
(3)合理转化:选择恰当的公式,促使差异的转化.
题型一:三角函数的基本概念
由于三角函数的基本概念是三角函数的基础,加上现在的教材对三角函数的要求有所降低,因而近几年在高考命题时,较少直接命制考查本节知识的题目。
例1、(2007年北京高考)已知 ,那么角
,那么角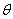 是( )
是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
解:
∵ ,∴当cosθ<0,tanθ>0时,θ∈第三象限;
,∴当cosθ<0,tanθ>0时,θ∈第三象限;
当cosθ>0,tanθ<0时,θ∈第四象限,选C.
例2、已知α是第二象限的角
(1)指出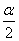 所在的象限,并用图象表示其变化范围;
所在的象限,并用图象表示其变化范围;
(2)若α还满足条件|α+2|≤4,求α的取值区间;
(3)若 ,求α-β的范围.
,求α-β的范围.
解:
依题意,2kπ+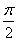 <α<2kπ+π(k∈Z).
<α<2kπ+π(k∈Z).
所以kπ+ <
< <kπ+
<kπ+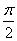 (k∈Z),若k为偶数,则
(k∈Z),若k为偶数,则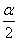 是第一象限的角;若k为奇数,则
是第一象限的角;若k为奇数,则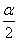 是第三象限的角;其变化范围如图中的阴影部分所示(不含边界).
是第三象限的角;其变化范围如图中的阴影部分所示(不含边界).
因为|α+2|≤4,所以-6≤α≤2,
即α∈(2kπ+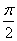 ,2kπ+π)∩[-6,2],
,2kπ+π)∩[-6,2],
结合数轴可知,α∈( ,-π)∪(
,-π)∪(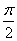 ,2].
,2].
(3)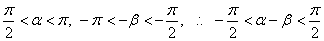 .
.
又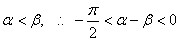 .
.
总结:
理解象限角、终边相同的角、区间角的概念,掌握α角的取值范围与2α、 角的取值范围间的相互关系.
角的取值范围间的相互关系.
题型二:同角三角函数关系式及诱导公式
同角三角函数的关系式和正弦、余弦的诱导公式是三角函数的基础知识,在高考中较少的直接命题,但在高考中充分体现了其工具性。
例3、(2007年安徽高考)已知0<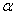 <
<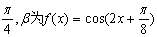 的最小正周期,a=(tan(
的最小正周期,a=(tan(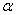 +
+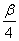 ),-1),b=(cosα,2),且a·b=m,求
),-1),b=(cosα,2),且a·b=m,求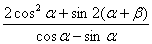 .
.
解:
因为 为
为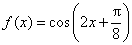 的最小正周期,故
的最小正周期,故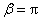 .
.
因 ,又
,又 .
.
故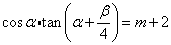 .由于
.由于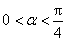 ,所以
,所以
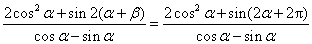
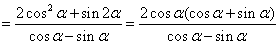
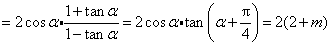 .
.
例4、(2005年湖南高考)已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.
解法一:
由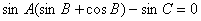 得
得
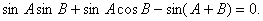
所以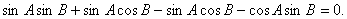 即
即
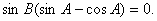
因为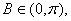 所以
所以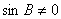 ,从而
,从而
由 知
知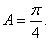 从而
从而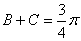 .
.
由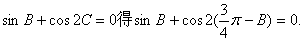
即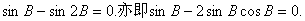
由此得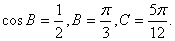
所以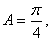
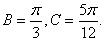
解法二:
由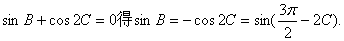
由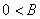 、
、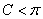 ,所以
,所以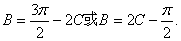
即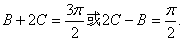
由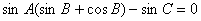 得
得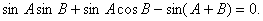
所以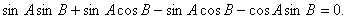
即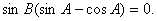
因为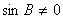 ,所以
,所以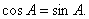
由 从而
从而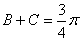 ,知B+2C=
,知B+2C=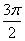 不合要求.
不合要求.
再由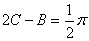 ,得
,得
所以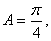
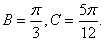
例5、是否存在α、β,α∈(-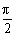 ,
, ),β∈(0,π)使等式sin(3π-α)=
),β∈(0,π)使等式sin(3π-α)=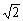 cos(
cos(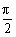 -β),
-β),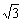 cos(-α)=-
cos(-α)=-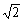 cos(π+β)同时成立?若存在,求出α、β的值;若不存在,请说明理由.
cos(π+β)同时成立?若存在,求出α、β的值;若不存在,请说明理由.
解:由条件得
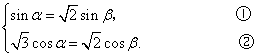
①2+②2得sin2α+3cos2α=2,∴cos2α= .
.
∵α∈(- ,
,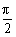 ),∴α=
),∴α=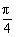 或α=-
或α=-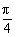 .
.
将α=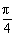 代入②得cosβ=
代入②得cosβ=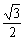 .又β∈(0,π),
.又β∈(0,π),
∴β=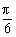 ,代入①可知,符合.
,代入①可知,符合.
将α=-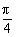 代入②得β=
代入②得β=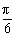 ,代入①可知,不符合.
,代入①可知,不符合.
综上可知α=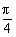 ,β=
,β=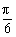 .
.
题型三:三角函数的图象问题
关于三角函数的图象问题,是高考考查的重点,近几年的考查有所加强,以选择题、填空题为主,有时会与三角变换及函数、平面向量等知识综合考查,内容上主要考查三角函数图象的变换、读图和识图以及图象的运用,周期性、单调性、奇偶性、对称性等内容.
例6、(2006年江苏高考)为了得到函数 的图像,只需把函数
的图像,只需把函数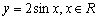 的图像上所有的点( )
的图像上所有的点( )
A.向左平移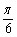 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
B.向右平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移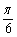 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
解:
先将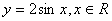 的图象向左平移
的图象向左平移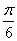 个单位长度,得到函数
个单位长度,得到函数 的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数
的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数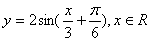 的图像.
的图像.
规律总结:
由函数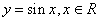 的图象经过变换得到函数
的图象经过变换得到函数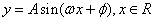 .
.
(1)y=Asinx,x∈R(A>0且A≠1)的图象可以看作把正弦曲线上的所有点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍得到的.
(2)函数y=sinωx, x∈R (ω>0且ω≠1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的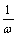 倍(纵坐标不变).
倍(纵坐标不变).
(3)函数y=sin(x+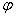 ),x∈R(其中
),x∈R(其中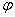 ≠0)的图象,可以看作把正弦曲线上所有点向左(当
≠0)的图象,可以看作把正弦曲线上所有点向左(当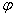 >0时)或向右(当
>0时)或向右(当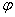 <0时)平行移动|
<0时)平行移动| |个单位长度而得到.(用平移法注意讲清方向:“加左”“减右”)
|个单位长度而得到.(用平移法注意讲清方向:“加左”“减右”)
可以先平移变换后伸缩变换,也可以先伸缩变换后平移变换,但注意:先伸缩时,平移的单位把x前面的系数提取出来.
例7、(2007年安徽高考) 函数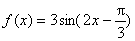 的图象为
的图象为 ,
,
①图象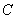 关于直线
关于直线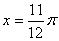 对称;
对称;
②函数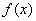 在区间
在区间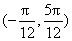 内是增函数;
内是增函数;
③由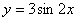 的图象向右平移
的图象向右平移 个单位长度可以得到图象
个单位长度可以得到图象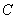 .
.
以上三个论断中,正确的论断的个数是( )
A.0 B.1 C.2 D.3
解:
①图象C关于直线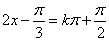 对称,当k=1时,图象C关于
对称,当k=1时,图象C关于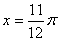 对称;①正确;②x∈
对称;①正确;②x∈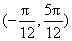 时,
时, ∈(-
∈(- ,
, ),∴函数
),∴函数 在区间
在区间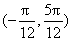 内是增函数;②正确;③由
内是增函数;②正确;③由 的图象向右平移
的图象向右平移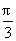 个单位长度可以得到
个单位长度可以得到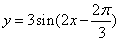 ,得不到图象C,③错误.
,得不到图象C,③错误.
∴正确的结论有2个,选C.
例8、(2007年湖南高考)已知函数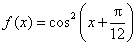 ,
, .
.
(I)设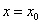 是函数
是函数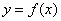 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值.
(II)求函数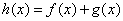 的单调递增区间.
的单调递增区间.
解:
(I)由题设知 .
.
因为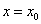 是函数
是函数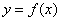 图象的一条对称轴,所以
图象的一条对称轴,所以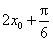
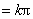 ,
,
即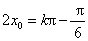 (
(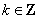 ).
).
所以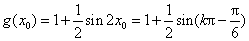 .
.
当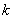 为偶数时,
为偶数时,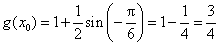 ,
,
当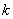 为奇数时,
为奇数时,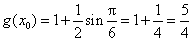 .
.
(II)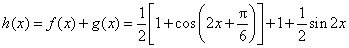
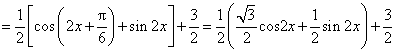
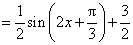 .
.
当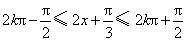 ,即
,即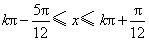 (
(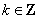 )时,
)时,
函数 是增函数,
是增函数,
故函数 的单调递增区间是
的单调递增区间是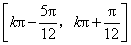 (
(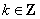 ).
).
例9.已知函数y=asinx+bcosx+c的图象上有一个最低点(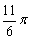 ,1),将图象上每点纵坐标不变,横坐标缩小到原来的
,1),将图象上每点纵坐标不变,横坐标缩小到原来的 倍,然后向左平移1个单位,得到y=f(x)的图象,且f(x)=3的所有正根依次为一个公差为3的等差数列,求f(x)的解析式,并求最小正周期和单调减区间.
倍,然后向左平移1个单位,得到y=f(x)的图象,且f(x)=3的所有正根依次为一个公差为3的等差数列,求f(x)的解析式,并求最小正周期和单调减区间.
解:

由f(x)=3的所有正根依次成等差数列,即曲线y=f(x)与直线y=3的相邻交点间的距离相等,根据三角函数的图象与性质,直线y=3要么与曲线y=f(x)相切,即过f(x)的最高点或最低点,要么过曲线的拐点(凹凸性改变的点),因为(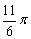 ,1)是图像上的最低点,故y=3与曲线y=f(x)在最高点相切.
,1)是图像上的最低点,故y=3与曲线y=f(x)在最高点相切.
当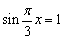 时,f(x)=2c-1=3,所以c=2,此时周期应为公差3,这与上面已知周期6矛盾,故舍去.
时,f(x)=2c-1=3,所以c=2,此时周期应为公差3,这与上面已知周期6矛盾,故舍去.
当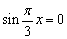 时,f(x)= c=3,此时周期6恰为公差3的2倍,符合题意.
时,f(x)= c=3,此时周期6恰为公差3的2倍,符合题意.
所以 .
.
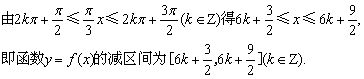
题型四:解斜三角形
三角形中的三角问题一直是高考的热点,一般难度不大,三种题型均有,主要考查正弦定理、余弦定理的应用以及三角恒等变换能力和运算能力.
例10.(2007年福建高考)在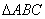 中,
中,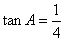 ,
,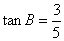 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若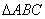 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
解:
(Ⅰ)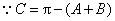 ,
,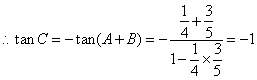 .
.
又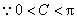 ,
,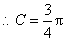 .
.
(Ⅱ)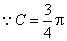 ,
,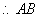 边最大,即
边最大,即 .
.
又 ,
,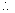 角A最小,BC边为最小边.
角A最小,BC边为最小边.
由 且
且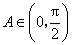 ,得
,得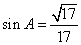 .由
.由 得:
得:
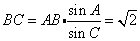 .所以,最小边
.所以,最小边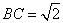 .
.
例11.在某海滨城市附近海面有一台风,据检测,当前台风中心位于城市O(如图)的东偏南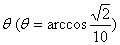 方向300 km的海面P处,并以20 km / h的速度向西偏北
方向300 km的海面P处,并以20 km / h的速度向西偏北 的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭.
的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭.
解法一:
设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60(km) .
若在时刻t城市O受到台风的侵袭,则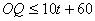 .
.
由余弦定理知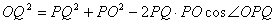 .
.
由于PO=300,PQ=20t.
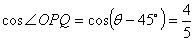 .
.
故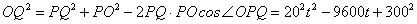 .
.
因此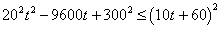 .
.
 .
.
解得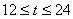 .
.
解法二:
建立坐标系:以O为原点,正东方向为x轴正向. 在时刻t(h)台风中心 的坐标为
的坐标为
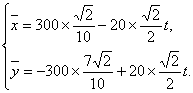
此时台风侵袭的区域是 ,其中
,其中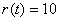 t+60,
t+60,
若在t时,该城市O受到台风的侵袭,则有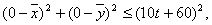
即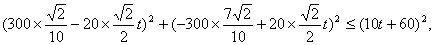
即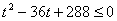 ,解得
,解得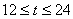 .
.
答:12小时后该城市开始受到台风侵袭.
专题小结
1.三角变换常用的方法技巧有切割化弦法,升幂降幂法、辅助元素法,“1”的代换法等.对于三角公式要记忆准确(在理解基础上),并要注意公式成立的条件,在应用时,要认真分析,合理转化,避免盲目性.
2.三角函数图象的对称性和有界性是高考命题的一个热点.最基本的三角函数图象的形状和位置特征,要准确掌握,它是利用数形结合思想解决三角函数问题的关键.三角函数图象各种变换的实质要熟练掌握,不能从形式上简单判断.
3.解三角形时,要根据条件正确选择正、余弦定理以及三角变换式.要充分发挥图形的作用,注意三角形外接圆半径在正弦定理中的转化功能.