|
一、复习策略
应用问题是指有实际背景或问题有实际意义的数学问题,解答数学应用题,需在理解题意的基础上,把问题转化为相应的数学问题,再根据要求求解.
1、解应用题的一般思路可表示如下:
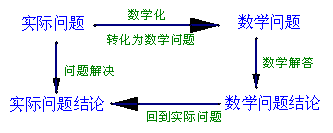
2、解应用题的一般程序:
(1)读:阅读理解文字表达的题意,分清条件和结论,理顺数量关系,这一关是基础.
(2)建:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型.熟悉基本数学模型,正确进行建“模”是关键的一关.
(3)解:求解数学模型,得到数学结论.一要充分注意数学模型中元素的实际意义,更要注意巧思妙作,优化过程.
(4)答:将数学结论还原给实际问题的结果.
3、中学数学中常见应用问题与数学模型
(1)优化问题:实际问题中的“优选”“控制”等问题,常需建立“不等式模型”和“线性规划”问题解决.
(2)预测问题:经济计划、市场预测这类问题通常设计成“数列模型”来解决.
(3)最(极)值问题:工农业生产、建设及实际生活中的极限问题常设计成“函数模型”,转化为求函数的最值.
(4)等量关系问题:建立“方程模型”解决.
(5)测量问题:可设计成“图形模型”利用几何知识解决.
4、解应用问题的一般步骤为:
(1)审题:理解题意,把握问题本质;
(2)建模:分析题中的数量关系,建立相应数学模型,将应用问题转化为数学问题;
(3)解模:用数学知识与方法解决转化了的数学问题;
(4)回归:回到应用问题,检验结果的实际意义,给出答案.
复习中应加强概率、函数、不等式、线性规划以及函数与不等式、函数与数列、数列与不等式等综合问题的训练.
二、典例剖析
(一)函数模型
(I)函数模型为正比例函数
例1、某服装个体户在进一批服装时,进价已按原价打了七五折,他打算对该批服装定一新价标在价目卡上,并注明按该价降价20%销售.这样,仍可获得25%的纯利.求这个个体户给这批服装定的新标价与原价之间的函数关系.
解:设原价为x元,新标价为y元.
则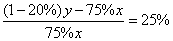 ,化简得 ,化简得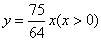 . .
(II)函数模型为反比例函数
例2、学校请了30个木工,要制作200把椅子和100张课桌,已知制作一张课桌与制作一把椅子的工时数之比为10∶7,问30名工人应当如何分配(一组做课桌,另一组做椅子),能使完成任务最快.
解:
设x个工人做课桌,则有(30- )个工人做椅子,一个工人在单位时间内可制作7a张课桌或10a把椅子,所以 )个工人做椅子,一个工人在单位时间内可制作7a张课桌或10a把椅子,所以
制作100张课桌所需的时间为函数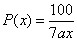 , ,
制作200把椅子所需的时间为函数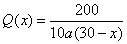 , ,
完成任务所需要的时间为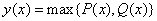 , ,
为求得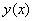 的最小值,需满足 的最小值,需满足 . .
即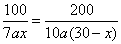 ,解得 ,解得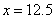 ,考虑到人数 ,考虑到人数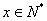 , ,
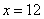 时, 时,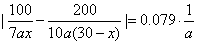 . .
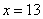 时, 时,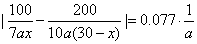 . .
所以用13个工人制作课桌,17名工人制作椅子完成任务最快.
(III)函数模型为一次函数
例3、我国是水资源比较贫乏的国家之一,各地采用价格调控手段以达到节约用水的目的.某市用水收费方法是:水费=基本费+超额费.该市规定:(1)若每户每月用水量不超过最低限量m立方米时,只付基本费9元和每月的定额损耗费a元;(2)若每户每月用水量超过m立方米时,除了付基本费和损耗费外,超过部分每立方米付n元的超额费;(3)每户每月的损耗费不超过5元.
(Ⅰ)求每户月水费y(元)与月用水量x(立方米)的函数关系;
(Ⅱ)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示,试分析一、二、三各月份的用水量是否超过最低限量,并求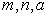 的值. 的值.
月份 |
用水量(立方米) |
水费(元) |
一 |
4 |
18 |
二 |
5 |
26 |
三 |
2.5 |
10 |
解:
(Ⅰ)由题意,每月用水量为x(立方米),支付费用y(元),则
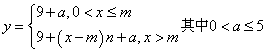 . .
(Ⅱ)∵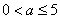 ,∴ ,∴ ,由表知,一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于最低限量 ,由表知,一、二月份的水费均大于14元,故用水量4立方米,5立方米都大于最低限量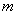 立方米,将 立方米,将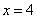 和 和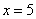 分别代入 分别代入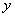 的解析式,得 的解析式,得
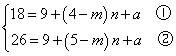
由②-①得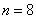 ,从而 ,从而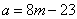 ③. ③.
又三月份用水量为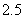 立方米,若 立方米,若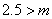 ,将 ,将 代入 代入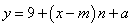 得 得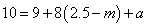 ,得 ,得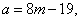 这与③矛盾,∴ 这与③矛盾,∴ ,即三月份用水量 ,即三月份用水量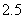 立方米没有超过最低限量.此时有 立方米没有超过最低限量.此时有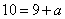 ,∴ ,∴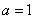 ,代入③得 ,代入③得 . .
综上:一、二月份用水量超过最低限量,三月份用水量没有超过最低限量,且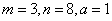 . .
说明:
(1)分析图表是数学应用的一个重要方面;
(2)本题中对三月份的用水量是否超过最低限量的分析采用了假设检验的思想,应好好体会.
例4、某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量 与时间 与时间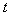 之间近似满足如图所示的曲线. 之间近似满足如图所示的曲线.
(1)写出服药后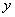 与 与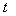 之间的函数关系式; 之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药时间为早晨7:00,问一天中怎样安排服药的时间(共4次)效果最佳?
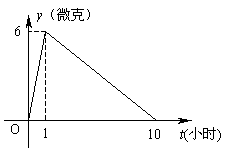
解:
(1)依题得,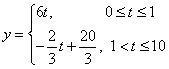 . .
(2)设第二次服药是在第一次服药后t1小时,则 ,因而第二次服药应在11︰00; ,因而第二次服药应在11︰00;
设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药量的和,即有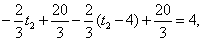 解得t2=9小时,故第三次服药应在16:00; 解得t2=9小时,故第三次服药应在16:00;
设第四次服药在第一次后t3小时(t3>10),则此时第一次服进的药已吸收完,此时血液中含药量应为第二、三次的和, 解得t3=13.5小时,故第四次服药应在20︰30. 解得t3=13.5小时,故第四次服药应在20︰30.
(IV)函数模型为二次函数
例5、已知某商品的价格上涨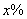 ,销售的数量就减少 ,销售的数量就减少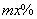 ,其中 ,其中 为正的常数. 为正的常数.
(1)当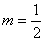 时,该商品的价格上涨多少,就能使销售的总金额最大? 时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求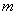 的取值范围. 的取值范围.
解:
(1)设商品现在定价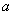 元,卖出的数量为 元,卖出的数量为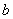 个. 个.
由题设:当价格上涨x%时,销售总额为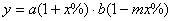 , ,
即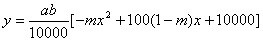 ,( ,( ), ),
取 得: 得: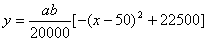 ,当 ,当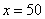 时, 时,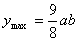 , ,
即:该商品的价格上涨50%时,销售总金额最大.
(2)二次函数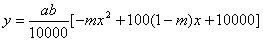 , ,
在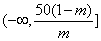 上递增,在 上递增,在 上递减, 上递减,
适当地涨价能使销售总金额增加,即在 内存在一个区间,使函数 内存在一个区间,使函数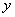 在此区间上是增函数,所以 在此区间上是增函数,所以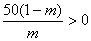 ,解得 ,解得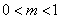 ,即所求 ,即所求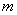 的取值范围是 的取值范围是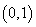 . .
例6、某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出. 当每辆车的月租金每增加50元时,未租出的车将会增加一辆. 租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:
(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为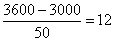 ,所以这时租出了88辆车. ,所以这时租出了88辆车.
(Ⅱ)设每辆车的月租金定为x元,则租赁公司的月收益为
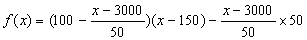 , ,
整理得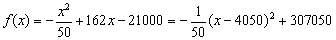 . .
所以,当x=4050时,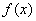 最大,最大值为 最大,最大值为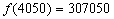 , ,
即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大月收益为307050元.
例7、距离船只A的正北方向100海里处有一船只B,以每小时20海里的速度沿北偏西60°角的方向行驶,A船只以每小时15海里的速度向正北方向行驶,两船同时出发,问几小时后两船相距最近?
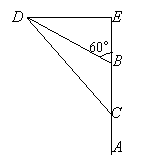
解:
设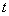 小时后 小时后 行驶到点 行驶到点 , , 行驶到点 行驶到点 ,则BD=20t, ,则BD=20t,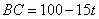 , ,
过 作 作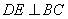 于 于 , ,
∴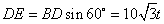 , ,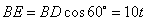 , ,
∴ , ,
∴
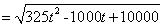 , ,
∴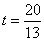 时 时 最小,最小值为 最小,最小值为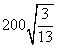 ,即两船行驶 ,即两船行驶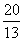 小时相距最近. 小时相距最近.
(V)函数模型为指数函数
例8、有一个受到污染的湖泊,其湖水的容积为V立方米,每天流出湖泊的水量都是r立方米,现假设下雨和蒸发正好平衡,且污染物质与湖水能很好地混合,用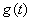 表示第 表示第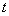 天每立方米湖水所含污染物质的克数,我们称为在第t天的湖水污染质量分数,已知目前污染源以每天p克的污染物质污染湖水,湖水污染质量分数满足关系式 天每立方米湖水所含污染物质的克数,我们称为在第t天的湖水污染质量分数,已知目前污染源以每天p克的污染物质污染湖水,湖水污染质量分数满足关系式 + + 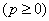 ,其中, ,其中,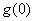 是湖水污染的初始质量分数. 是湖水污染的初始质量分数.
(1)当湖水污染质量分数为常数时,求湖水污染的初始质量分数;
(2)求证:当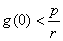 时,湖泊的污染程度将越来越严重; 时,湖泊的污染程度将越来越严重;
(3)如果政府加大治污力度,使得湖泊的所有污染停止,那么需要经过多少天才能使湖水的污染水平下降到开始时污染水平的5%?
解:
(1)∵ 为常数,有 为常数,有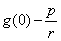 =0,∴ =0,∴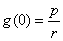 . .
(2) 设0<t1<t2,则
g(t1)-g(t2)=[g(0)-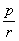 ] ]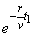 -[g(0)- -[g(0)-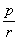 ] ]
=[g(0)-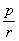 ][ ][ - -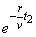 ] ]
=[g(0)-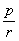 ] ] , ,
∵ <0,t1<t2, <0,t1<t2,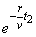 > >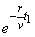 ,∴ ,∴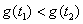 . .
故湖水污染质量分数随时间变化而增加,污染越来越严重.
(3)污染停止即P=0,g(t)=g(0)·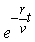 ,设经过t天能使湖水污染下降到初始污染水平5%即g(t)=5% g(0). ,设经过t天能使湖水污染下降到初始污染水平5%即g(t)=5% g(0).
∴ = =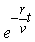 ,∴t= ,∴t=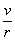 ln20, ln20,
故需要 ln20天才能使湖水的污染水平下降到开始时污染水平的5%. ln20天才能使湖水的污染水平下降到开始时污染水平的5%.
(VI)函数模型为其它函数
例9、一批零兼营的文具商店规定:凡购买铅笔51支以上(含51支),按批发价结算,而少于51支则按零售价结算,批发价每购60支比零售60支少付一元.现有班长来购铅笔,若给全班每人购一支,需支付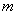 元( 元(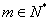 ),但若多买10支,则可按批发价结算,恰好也支付 ),但若多买10支,则可按批发价结算,恰好也支付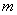 元,问该班有多少学生? 元,问该班有多少学生?
解:
设全班有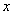 人,根据题意设 人,根据题意设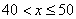 ,则铅笔零售价为 ,则铅笔零售价为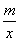 元,批发价为 元,批发价为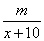 , ,
则根据题意,有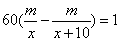 ,整理得 ,整理得
 ① ①
由函数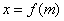 的定义域,值域得 的定义域,值域得
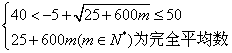 , ,
解得 ,代入①得 ,代入①得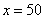 ,∴该班有50个学生. ,∴该班有50个学生.
例10、某工厂生产一种机器的固定成本为5000元,且每生产1台需要增加投入25元,销售后,为了对今后的销售提供参考的数据,对销售市场进行调查后得知,市场对此产品的需求量为每年500台,已知销售收入函数为:
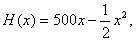 其中x是产品售出的数量,且 其中x是产品售出的数量,且 . .
(I)若x为年产量,y为利润,求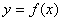 的解析式; 的解析式;
(II)当年产量为何值时,工厂的年利润最大,其最大值是多少?
解:
(I) ,产品全部售出;当 ,产品全部售出;当 时,产品只能售出500台, 时,产品只能售出500台,
故
(II)当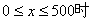

(二)数列模型
例11、一艘太空飞船飞往地球.第一次观测时发现一个正三角形的岛屿(我们记其边长为1);第二次观测时,发现它并非正三角形,而是每边中央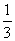 处向外有一正三角形海峡,形成正六边形;第三次观测时,发现原先每一小边的中央 处向外有一正三角形海峡,形成正六边形;第三次观测时,发现原先每一小边的中央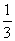 处都有一向外突出的海峡(正三角形、如图),……,把这个过程无限继续下去,就得到著名的教学模型——柯克岛. 处都有一向外突出的海峡(正三角形、如图),……,把这个过程无限继续下去,就得到著名的教学模型——柯克岛.
(1)把第k次观测到的岛的面积记为ak,{ak}有无极限?如果我们把这个极限叫岛的面积,柯克岛的面积是多少?
(2)把第k次观测到的岛的海岸线长记为bk,求{bk}的通项公式,{bk}有无极限?如果把此极限当作柯克岛的海岸线长,它是多少?
(3)以上结果能说明什么问题?

解:
(1)记 ck为第k次观测时的边数,c1=3,由于每一边中央突起一个三角形,即每一边变为4条边,故ck+1=4ck,从而第k次观测时,柯克岛的边数是ck=3·4k-1,(k∈N),
又以边长为dk,则dk+1= dk,∴ {dk}成等比数列,公比为 dk,∴ {dk}成等比数列,公比为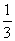 , d1=1, , d1=1,
∴ dk=(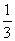 )k-1, )k-1,
∴ ak+1=ak+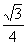 ·( ·(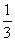 dk)2·3·4k-1=ak+ dk)2·3·4k-1=ak+ , ,
∴ an=(an-an-1)+(an-1-an-2)+……+(a2-a1)+a1
= = =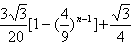 . .
所以,an的极限存在,且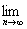 an= an=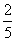 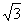 . .
(2)由(1)可知 bk=ck·dk=3×4k-1×( )k-1=3·( )k-1=3·(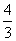 )k-1, )k-1,
所以,{bn}是等比数列,且公比q= >1.故{bn}的极限不存在. >1.故{bn}的极限不存在.
(3)以上结果说明了一个面积有限的平面区域的周界长度可以是无限的.
三、解析几何模型
例12、有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)
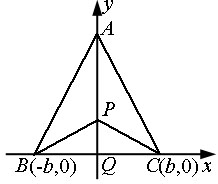
(Ⅰ)若希望点P到三镇距离的平方和为最小,点P应位于何处?
(Ⅱ)若希望点P到三镇的最远距离为最小,点P应位于何处?
(Ⅰ)解:设P的坐标为(0,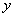 ),则P至三镇距离的平方和为 ),则P至三镇距离的平方和为
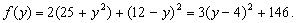
所以,当 时,函数 时,函数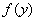 取得最小值. 取得最小值.
答:点P的坐标是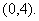
(Ⅱ)解法一:P至三镇的最远距离为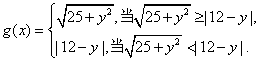
由 解得 解得 记 记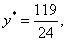 于是 于是 因为 因为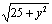 在[ 在[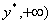 上是增函数,而 上是增函数,而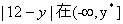 上是减函数. 所以 上是减函数. 所以 时,函数 时,函数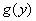 取得最小值. 取得最小值.
答:点P的坐标是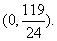
解法二:P至三镇的最远距离为
由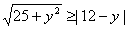 解得 解得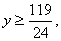 记 记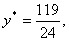 于是 于是

函数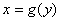 的图象如图 的图象如图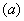 ,因此, ,因此,
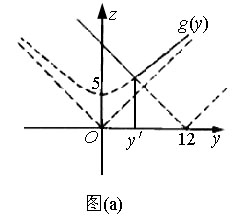
当y=y′时,函数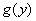 取得最小值. 取得最小值.
答:点P的坐标是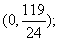
解法三:因为在△ABC中,AB=AC=13,
且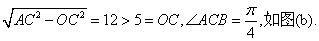
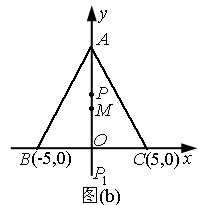
所以△ABC的外心M在线段AO上,其坐标为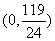 , ,
且AM=BM=CM. 当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,这时P到A、B、C三点的最远距离为P1C和P2A,且P1C≥MC,P2A≥MA,所以点P与外心M重合时,P到三镇的最远距离最小.
答:点P的坐标是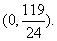 - 返回 -
|