|
一、复习策略
高考圆锥曲线试题一般有3题(1个选择题, 1个填空题, 1个解答题),共计22分左右,考查的知识点约为20个左右. 其命题一般紧扣课本,突出重点,全面考查. 选择题和填空题考查以圆锥曲线的基本概念和性质为主,难度在中等以下,一般较容易得分,解答题重点考查圆锥曲线中的综合问题.圆锥曲线的综合问题包括:解析法的应用,与圆锥曲线有关的定值问题、最值问题、参数问题、应用题和探索性问题,圆锥曲线知识的纵向联系,圆锥曲线知识和三角、向量等代数知识的横向联系,解答这部分试题,需要较强的代数运算能力和图形认识能力,要能准确地进行数与形的语言转换和运算,推理转换,并在运算过程中注意思维的严密性,以保证结果的完整.
解决圆锥曲线综合题,关键是熟练掌握每一种圆锥曲线的定义、标准方程、图形与几何性质,注意挖掘知识的内在联系及其规律,通过对知识的重新组合,以达到巩固知识、提高能力的目的.
(1) 当直线与圆锥曲线相交时:涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
(2)对于求曲线方程中参数的取值范围问题,需构造参数满足的不等式,通过求不等式(组)求得参数的取值范围;或建立关于参数的目标函数,转化为函数的值域.
(3)对于圆锥曲线的最值问题,解法常有两种:当题目的条件和结论能明显体现几何特征及意义,可考虑利用数形结合法解;当题目的条件和结论能体现一种明确的函数关系,则可先建立目标函数,再求这个函数的最值.
二、典例剖析
题型一:与圆锥曲线定义有关的问题
例1.(2008年北京高考)若点P到直线x=-1的距离比它到点(2,0)的距离小1,则点P的轨迹为( )
A.圆 B.椭圆 C.双曲线 D.抛物线
答案:D
例2.P是双曲线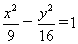 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( ) 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
A. 6 B.7 C.8 D.9
答案:D
解:
设双曲线的两个焦点分别是F1(-5,0)与F2(5,0),则这两点正好是两圆的圆心,当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大,此时|PM|-|PN|=(|PF1|+2)-(|PF2|-1)=6+3=9,故选D.
题型二:求圆锥曲线的标准方程、离心率、准线方程等
例3.设F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为( )
A.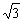 -1 B.2- -1 B.2-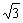 C. C.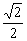 D. D.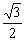
答案:A
解:易知圆F2的半径为c,(2a-c)2+c2=4c2,(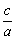 )2+2( )2+2(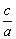 )-2=0, )-2=0,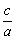 = =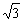 -1. -1.
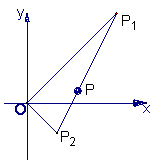
例4.如图,已知△P1OP2的面积为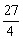 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为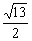 的双曲线方程. 的双曲线方程.
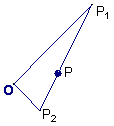
解:以O为原点,∠P1OP2的角平分线为x轴建立如图的直角坐标系.
设双曲线方程为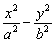 =1(a>0,b>0). =1(a>0,b>0).
由e2=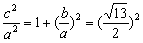 ,得 ,得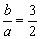 . .
∴两渐近线OP1、OP2方程分别为y=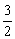 x和y=- x和y=-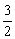 x. x.
设点P1(x1,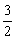 x1),P2(x2,- x1),P2(x2,-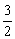 x2)(x1>0,x2>0),则由点P分 x2)(x1>0,x2>0),则由点P分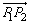 所成的比λ= 所成的比λ=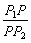 =2,得P点坐标为( =2,得P点坐标为(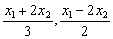 ),又点P在双曲线 ),又点P在双曲线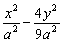 =1上,所以 =1上,所以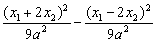 =1, =1,
即(x1+2x2)2-(x1-2x2)2=9a2,整理得8x1x2=9a2.①
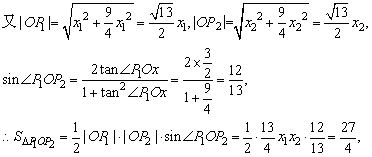
即x1x2=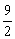 .② .②
由①、②得a2=4,b2=9,故双曲线方程为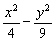 =1. =1.
题型三:直线与圆锥曲线的位置关系
例5.如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为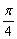 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积. 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
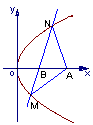
解法一:由题意,可设l的方程为y=x+m,其中-5<m<0.
由方程组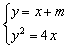 ,消去y,得x2+(2m-4)x+m2=0 ① ,消去y,得x2+(2m-4)x+m2=0 ①
∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式Δ=(2m-4)2-4m2=16(1-m)>0,
解得m<1,又-5<m<0,∴m的范围为(-5,0).
设M(x1,y1),N(x2,y2)则x1+x2=4-2m,x1·x2=m2,
∴|MN|=4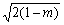 . .
点A到直线l的距离为d=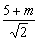 . .
∴S△=2(5+m)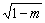 ,从而S△2=4(1-m)(5+m)2. ,从而S△2=4(1-m)(5+m)2.
=2(2-2m)·(5+m)(5+m)≤2(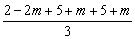 )3=128. )3=128.
∴S△≤8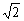 ,当且仅当2-2m=5+m,即m=-1时取等号. ,当且仅当2-2m=5+m,即m=-1时取等号.
故直线l的方程为y=x-1,△AMN的最大面积为8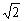 . .
解法二:由题意,可设l与x轴相交于B(m,0),l的方程为x = y+m,其中0<m<5.
由方程组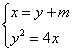 ,消去x,得y2-4y-4m=0 ① ,消去x,得y2-4y-4m=0 ①
∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式Δ=(-4)2+16m=16(1+m)>0必成立,
设M(x1,y1),N(x2,y2)则y1+y2=4,y1·y2=-4m,
∴S△=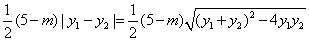
=4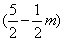 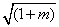 =4 =4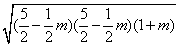
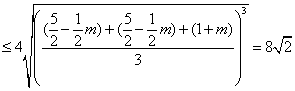 . .
∴S△≤8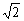 ,当且仅当 ,当且仅当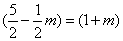 即m=1时取等号. 即m=1时取等号.
故直线l的方程为y=x-1,△AMN的最大面积为8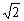 . .
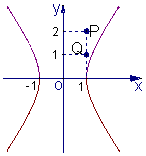
例6.已知双曲线C:2x2-y2=2与点P(1,2).
(1)求过P(1,2)点的直线l的斜率取值范围,使l与C分别有一个交点,两个交点,没有交点.
(2)若Q(1,1),试判断以Q为中点的弦是否存在.
解:
(1)当直线l的斜率不存在时,l的方程为x=1,与曲线C有一个交点.当l的斜率存在时,设直线l的方程为y-2=k(x-1),代入C的方程,并整理得
(2-k2)x2+2(k2-2k)x-k2+4k-6=0 (*)
(ⅰ)当2-k2=0,即k=±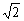 时,方程(*)有一个根,l与C有一个交点. 时,方程(*)有一个根,l与C有一个交点.
(ⅱ)当2-k2≠0,即k≠±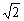 时 时
Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k).
①当Δ=0,即3-2k=0,k=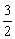 时,方程(*)有一个实根,l与C有一个交点. 时,方程(*)有一个实根,l与C有一个交点.
②当△>0,即k<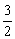 ,又k≠± ,又k≠±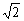 ,故当k<- ,故当k<-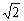 或- 或-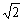 <k< <k<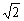 或 或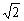 <k< <k<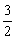 时,方程(*)有两不等实根,l与C有两个交点. 时,方程(*)有两不等实根,l与C有两个交点.
③当Δ<0,即k>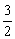 时,方程(*)无解,l与C无交点. 时,方程(*)无解,l与C无交点.
综上知:当k=±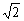 ,或k= ,或k=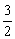 ,或k不存在时,l与C只有一个交点; ,或k不存在时,l与C只有一个交点;
当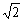 <k< <k< ,或- ,或-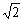 <k< <k<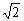 ,或k<- ,或k<-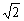 时,l与C有两个交点; 时,l与C有两个交点;
当k>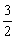 时,l与C没有交点. 时,l与C没有交点.
(2)假设以Q为中点的弦存在,设为AB,且A(x1,y1),B(x2,y2),则2x12-y12=2,2x22-y22=2两式相减得:2(x1-x2)(x1+x2)=(y1-y2)(y1+y2).
又∵x1+x2=2,y1+y2=2,∴2(x1-x2)=y1-y2 即kAB=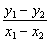 =2. =2.
但渐近线斜率为±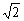 ,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在. ,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在.
题型四:圆锥曲线中的定值问题
例7.(08安徽)设椭圆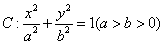 过点 过点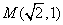 ,且左焦点为 ,且左焦点为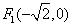 . .
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点P(4,1)的动直线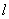 与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足 与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足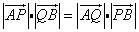 ,证明:点Q总在某定直线上. ,证明:点Q总在某定直线上.
解:(Ⅰ)由题意:
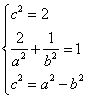 ,解得a2=4,b2=2,所求椭圆方程为 ,解得a2=4,b2=2,所求椭圆方程为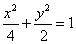 . .
(Ⅱ)方法一:设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题设知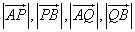 均不为零,记 均不为零,记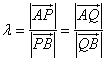 ,则 ,则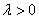 且 且 . .
又A、P、B、Q四点共线,从而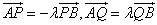 . .
于是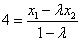 , ,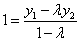 . .
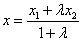 , ,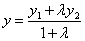 . .
从而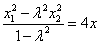 , (1) , (1)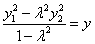 , (2) , (2)
又点A、B在椭圆C上,即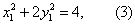
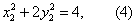
(1)+(2)×2并结合(3),(4)得4x+2y=4,
即点Q(x,y)总在定直线2x+y-2=0上.
方法二:设点Q(x,y),A(x1,y1),B(x2,y2).由题设,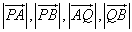 均不为零. 均不为零.
且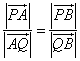
又P,A,Q,B四点共线,可设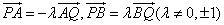 ,于是 ,于是
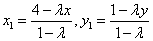 (1) (1)
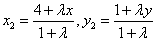 (2) (2)
由于A(x1,y1),B(x2,y2)在椭圆C上,将(1)(2)分别代入C的方程x2+2y2=4,整理得
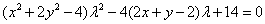 (3) (3)
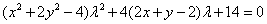 (4) (4)
(4)-(3)得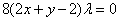 . .
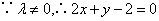 ,即点Q(x,y)总在定直线2x+y-2=0上. ,即点Q(x,y)总在定直线2x+y-2=0上.
题型五:圆锥曲线中的最值问题
例8.如图,已知椭圆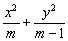 =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||. =1(2≤m≤5),过其左焦点且斜率为1的直线与椭圆及其准线的交点从左到右的顺序为A、B、C、D,设f(m)=||AB|-|CD||.
(1)求f(m)的解析式;
(2)求f(m)的最值.
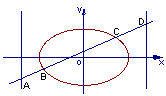
解:
(1)设椭圆的半长轴、半短轴及半焦距依次为a、b、c,则a2=m,b2=m-1,c2=a2-b2=1.
∴椭圆的焦点为F1(-1,0),F2(1,0).
故直线的方程为y=x+1,又椭圆的准线方程为x=±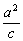 ,即x=±m. ,即x=±m.
∴A(-m,-m+1),D(m,m+1).
考虑方程组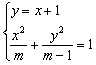 ,消去y得:(m-1)x2+m(x+1)2=m(m-1). ,消去y得:(m-1)x2+m(x+1)2=m(m-1).
整理得:(2m-1)x2+2mx+2m-m2=0.
Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2.
∵2≤m≤5,∴Δ>0恒成立,xB+xC=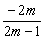 . .
又∵A、B、C、D都在直线y=x+1上.
∴|AB|=|xB-xA|·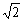 =(xB-xA)· =(xB-xA)·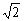 ,|CD|= ,|CD|=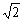 (xD-xC). (xD-xC).
∴||AB|-|CD||=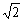 |xB-xA+xC-xD|= |xB-xA+xC-xD|=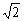 |(xB+xC)-(xA+xD)|. |(xB+xC)-(xA+xD)|.
又∵xA=-m,xD=m,∴xA+xD=0.
∴||AB|-|CD||=|xB+xC|·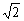 =| =|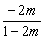 |· |·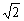 = =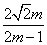 (2≤m≤5). (2≤m≤5).
故f(m)=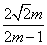 ,m∈[2,5]. ,m∈[2,5].
(2)由f(m)= 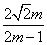 ,可知f(m)= ,可知f(m)=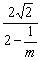 . .
又2-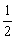 ≤2- ≤2-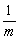 ≤2- ≤2-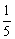 ,∴f(m)∈ ,∴f(m)∈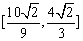 . .
故f(m)的最大值为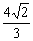 ,此时m=2;f(m)的最小值为 ,此时m=2;f(m)的最小值为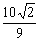 ,此时m=5. ,此时m=5.
题型六:多曲线的综合问题
例9.已知椭圆C1: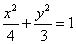 ,抛物线C2: ,抛物线C2: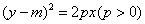 ,且C1、C2的公共弦AB过椭圆C1的右焦点. ,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥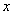 轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上; 轴时,求m、p的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在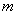 、 、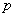 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说明理由. 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m、p的值;若不存在,请说明理由.
解:
(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为 x=1,
从而点A的坐标为(1,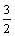 )或(1,- )或(1,-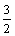 ). ).
因为点A在抛物线上,所以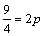 ,即 ,即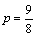 . .
此时C2的焦点坐标为(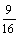 ,0),该焦点不在直线AB上. ,0),该焦点不在直线AB上.
(II)解法一:假设存在m、p的值使C2的焦点恰在直线AB上,由(I)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1).
由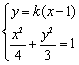 消去y得 消去y得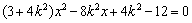 ① ①
设A、B的坐标分别为(x1,y1), (x2,y2),则x1,x2是方程①的两根,x1+x2=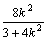 . .
由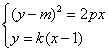
消去y得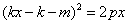 . ② . ②
因为C2的焦点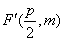 在直线 在直线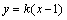 上, 上,
所以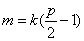 ,即 ,即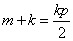 .代入②有 .代入②有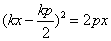 . .
即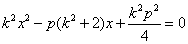 . ③ . ③
由于x1,x2也是方程③的两根,所以x1+x2=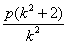 . .
从而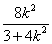 = =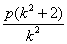 .解得 .解得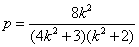 ④ ④
又AB过C1、C2的焦点,所以
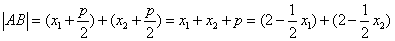 , ,
则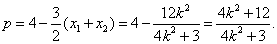 ⑤ ⑤
由④、⑤式得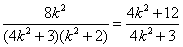 ,即k4-5k2-6=0. ,即k4-5k2-6=0.
解得k2=6. 于是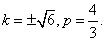
因为C2的焦点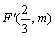 在直线 在直线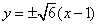 上,所以 上,所以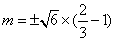 . .
∴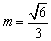 或 或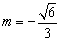 . .
由上知,满足条件的m、p存在,且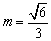 或 或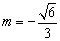 , ,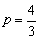 . .
解法二:设A、B的坐标分别为(x1,y1),(x2,y2).
因为AB既过C1的右焦点F(1,0),又过C2的焦点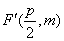 , ,
所以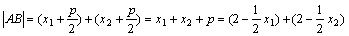 . .
即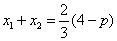 . ① . ①
由(Ⅰ)知x1≠x2,p≠2,于是直线AB的斜率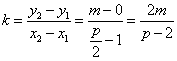 , ② , ②
且直线AB的方程是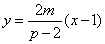 , ,
所以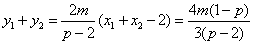 . ③ . ③
又因为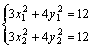 ,所以 ,所以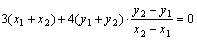 . ④ . ④
将①、②、③代入④得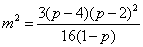 . ⑤ . ⑤
因为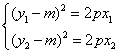 ,所以 ,所以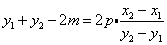 . ⑥ . ⑥
将②、③代入⑥得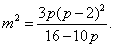 ⑦ ⑦
由⑤、⑦得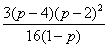 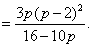 即 即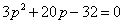 . .
解得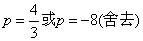 .将 .将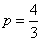 代入⑤得 代入⑤得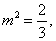
∴ 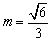 或 或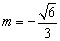 . .
由上知,满足条件的m、p存在,且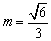 或 或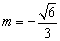 , ,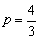 . . - 返回 -
|