近几年来,本章的内容在高考中都有所涉及,特别是带电粒子在磁场力作用下的圆周运动,几乎成为必考内容.加强对与该知识点有关联的习题训练,并掌握一般解题方法,对高考取得好成绩至关重要.
一、重难点分析
本章内容为历年高考的重点之一.高考涉及到内容主要有五个概念:磁感应强度、磁感线、磁通量、安培力、洛伦兹力;两个定则:安培定则和左手定则;三个模型;质谱仪、回旋加速器和磁流体发电机.纵观近几年的高考题,可以发现本章部分以考查基本概念和洛伦兹力的内容较多,对于知识的应用方向,一般考查磁场对通电导体受到安培力,分析通电线圈在磁场中受磁场力的合力,带电粒子在磁场中或在复合场中的运动问题.
纵观近五年的高考,分析高考考试大纲,在复习中要掌握以下知识:
1、磁感应强度:在磁场中垂直于磁场方向的通电直导线,受到的磁场力F与电流和导线长度的乘积的比值叫通电导线所在处的磁感应强度.大小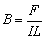 ,方向为该处磁场的方向.磁感应强度是客观存在的,与L的大小及有无没有关系,L又可称为电流元. ,方向为该处磁场的方向.磁感应强度是客观存在的,与L的大小及有无没有关系,L又可称为电流元.
2、磁感线:是为了形象的描述磁场而人为假设的曲线,并不是客观存在于磁场中的真实曲线;磁感线的疏密表示磁场的强弱,密的地方磁场强,疏的地方磁场弱,磁感线上某点的切线方向表示磁场的方向;磁感线不相交也不相切;所有磁场的磁感线都是闭合的.
3、磁通量:穿过某一面的磁感线的条数叫穿过该面的磁通量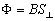 ,根据 ,根据 可知磁感应强度又可叫磁通密度. 可知磁感应强度又可叫磁通密度.
4、安培力:磁场对电流的作用力叫安培力,其大小F=BIL式中F、B、L要两两垂直,方向由左手定则判定.公式中F、B、L不两两垂直时可分解B或把L投影,当L弯曲时可取它的有效长度.
5、洛伦兹力:运动电荷在磁场中受到的磁场力叫洛伦兹力.当电荷的运动速度方向与磁场垂直时,洛伦兹力的大小F=qvB,洛伦兹力的方向用左手定则判定.安培力是洛伦兹力的宏观表现,洛伦兹力的方向始终与速度的方向垂直,洛伦兹力对运动电荷不做功.
6、带电粒子在匀强磁场中的圆周运动:带电粒子以速度v垂直射入匀强磁场B中,若只受洛伦兹力作用,则带电粒子在与B垂直的平面内做匀速圆周运动.洛伦兹力F提供向心力,由牛顿第二定律得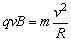 ,所以 ,所以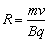 ,运动周期 ,运动周期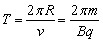 .圆心的确定:可以在圆弧上任意确定两个点的速度方向,根据洛伦兹力和速度垂直,则这两个洛伦兹力的交点就是圆心;也可以在圆弧上任意确定两个点作出它们之间弦的中垂线,则圆心一定在中垂线上;半径的确定:一般作出几何图形根据几何知识求解;在磁场中运动时间的确定,确定带电粒子所通过的圆弧的圆心角θ,则 .圆心的确定:可以在圆弧上任意确定两个点的速度方向,根据洛伦兹力和速度垂直,则这两个洛伦兹力的交点就是圆心;也可以在圆弧上任意确定两个点作出它们之间弦的中垂线,则圆心一定在中垂线上;半径的确定:一般作出几何图形根据几何知识求解;在磁场中运动时间的确定,确定带电粒子所通过的圆弧的圆心角θ,则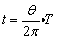 . .
7、带电粒子在复合场中的运动:当带电粒子受到的合外力为零时,带电粒子处于静止状态或匀速直线运动状态;当带电粒子受到的合外力只提供向心力时,粒子做匀速圆周运动;当带电粒子受到的合外力不断变化,且与速度方向不在同一直线上,粒子作不规则的曲线运动.可以应用牛顿运动定律、运动学、动量、能量等知识解题.
二、典型例题
例1、(2005·江苏)把长L=0.15m的导体棒置于磁感应强度B=1.0×10-2T的匀强磁场中,使导体棒和磁场方向垂直,如图所示,若导体棒中的电流I=2.0A,方向向左,则导体棒受到的安培力大小F=_____N,安培力的方向为竖直向_____.(选填“上”或“下”)
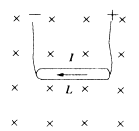
解析:
由安培力的公式得:F=BIL=1.0×10-2×2.0×0.15N=3×10-3N,由左手定则可判定,安培力方向竖直向下.
答案:3×10-3N 下
例2、(’05全国)在同时存在匀强电场和匀强磁场的空间中取正向坐标系Oxyz(z轴正方向竖直向上),如图所示.已知电场方向沿z轴正方向,场强大小为E;磁场方向沿y轴正方向,磁感应强度的大小为B;重力加速度为g.问:一质量为m,带电量为+q的质点从原点出发能否在坐标轴(x、y、z)上以速度v作匀速运动?若能,m、q、E、B、v及g应满足怎样的关系?若不能,说明理由.
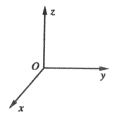
解析:
已知带电质点受到的电场力为qE,方向沿z轴正方向;质点受到的重力为mg,沿z轴负方向.
假设质点在x轴上做匀速运动,则它受的洛伦兹力必沿z轴正方向(当v沿x轴正方向)或沿z轴负方向(当v沿x轴负方向),要质点做匀速运动必分别有
qvB+qE=mg ①
或qE=qvB+mg ②
假设质点在y轴上做匀速运动,则无论沿y轴正方向还是负方向,洛伦兹力都为0,要质点做匀速运动必有qE=mg ③
假设质点在z轴上做匀速运动,则它受的洛伦兹力必平行于x轴,而电场力和重力都平行于z轴,三力的合力不可能为0,与假设矛盾,故质点不可能在z轴上做匀速运动.
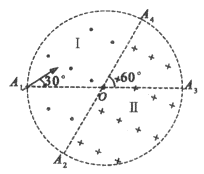
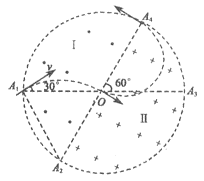
例3、(’05广东)如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进入Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t,求Ⅰ区和Ⅱ区中磁感应强度的大小(忽略粒子重力).
解析:
设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,用B1、B2、R1、R2、T1、T2分别表示在磁场Ⅰ区和Ⅱ区中磁感应强度、轨道半径和周期
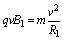 ① ①
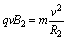 ② ②
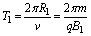 ③ ③
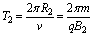 ④ ④
设圆形区域的半径为r.如图所示,已知带电粒子过圆心且垂直A2A4进入Ⅱ区磁场.连接A1A2,ΔA1OA2为等边三角形,A2为带电粒子在Ⅰ区磁场中运动轨迹的圆心,其轨迹的半径R1=A1A2=OA2=r ⑤
圆心角∠A1A2O=60°,带电粒子在Ⅰ区磁场中运动的时间为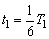 ⑥ ⑥
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即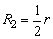 ⑦ ⑦
在Ⅱ区磁场中运动的时间为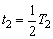 ⑧ ⑧
带电粒子从射入到射出磁场所用的总时间t=t1+t2 ⑨
由以上各式可得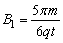 ⑩ ⑩
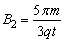 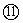
点评:
带电粒子在磁场中的运动问题的关键是确定圆心和半径,圆心的确定可以根据几何知识:圆心必在弦的中垂线上,两不同点的切线的垂线的交点是圆心;求带电粒子在磁场中运动的时间,可以求粒子轨迹是整个圆周的几分之几,然后时间就是周期的几分之几.
例4、(’04湖北)如图所示,在y>0的空间中存在匀强电场,场强沿y轴负方向;在y<0的空间中,存在匀强磁场,磁场方向垂直xy平面(纸面)向外.一电量为q、质量为m的带正电的运动粒子,经过y轴上y=h处的点P1时速度为v0,方向沿x轴正方向;然后,经过x轴上x=2h处的P2点进入磁场,并经过y轴上y=-2h处的P3点.不计重力.求:
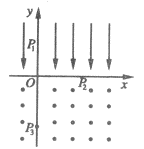
(1)电场强度的大小.
(2)粒子到达P2时速度的大小和方向.
(3)磁感应强度的大小.
解析:
(1)粒子在电场、磁场中运动的轨迹如图所示.设粒子从P1到P2的时间为t,电场强度的大小为E,粒子在电场中的加速度为a,由牛顿第二定律及运动学公式有
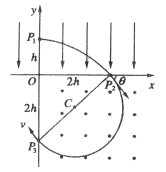
qE=ma ①
v0t=2h ②
 ③ ③
由①,②,③式解得
(2)粒子到达P2时速度沿x方向的分量仍为v0,以v1表示速度沿y方向分量的大小,v表示速度的大小,θ表示速度和x轴的夹角,则有
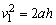 ④ ④
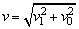 ⑤ ⑤
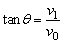 ⑥ ⑥
由②、③、④式得v1= v0 ⑦
由⑤、⑥、⑦式得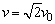 ⑧ ⑧
θ=45°
(3)设磁场的磁感应强度为B,在洛伦兹力作用下粒子做匀速圆周运动,由牛顿第二定律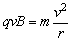 ⑨ ⑨
r是圆周的半径.此圆周与x轴和y轴的交点分别为P2、P3、因为OP2=OP3,θ=45°,由几何关系可知,连线P2P3为圆轨道的直径,由此可求得
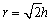 ⑩ ⑩
由⑧、⑨、⑩可得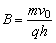
点评:
带电粒子电场中的运动可以用平抛运动的知识求解;解带电粒子在磁场中运动问题时,先要正确确定圆周运动的圆心和半径,圆心的确定可以分别作出不同位置的两个速度的垂线,两个垂线的交点就是圆心,也可以先找到圆周的弦,作出该弦的中垂线,则圆心一定在该中垂线上;半径的确定可以在确定圆心的基础上,作出几何图形根据几何知识求解.
例5、如图中①所示,把轻质导线圈用细线挂在磁铁N极附近,磁铁的轴线穿过线圈的圆心且垂直于线圈的平面.当线圈内通过图示方向的电流时,线圈将怎样运动?

解析:
(1)等效法:把环形电流等效成图②所示的条形磁铁P,可见两条形磁铁只是相互吸引而没有转动.
(2)利用结论法:把条形磁铁等效成图③所示的环形电流,由图可见两电流相互平行,方向相同,故两环形电流没有转动,只有相互吸引,即线圈将向磁铁平移.
例6、在xOy平面内有许多电子(质量为m,电量为e)从坐标原点O不断地以相同大小的速度v0沿不同的方向射入第Ⅰ象限,如图所示.现加上一个垂直于xOy平面的磁感强度为B的匀强磁场,要求这些电子穿过该磁场后都能平行于x轴向x轴正方向运动.试求出符合条件的磁场的最小面积.
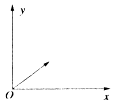
解析:
所有电子在所求的匀强磁场中均做匀速圆周运动,半径为R=mv0/eB,设与x轴成α角入射的电子从坐标为(x,y)的P点射出磁场,则有
x2+(R-y)2=R2 ①
①式即为电子离开磁场的下边界b时的表达式,当α=90°时,电子运动轨迹为磁场的上边界α,其表达式为(R-x)2+y2=R2 ②
其①、②式所确定的面积就是磁场的最小范围,如图所示,其面积为
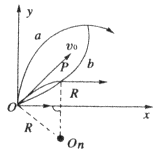
S=2(πR2/4-R2/2)=( π-2)(mv0/eB)2/2.
答案:S=(π-2)(mv0/eB)2/2
例7、一带电质点,质量为m,电荷量为q,以平行于Ox轴的速度v从y轴上的A点射入图中第一象限所示的区域.为了使该质点能从x轴上的B点以垂直于Ox轴的速度v射出,可在第一象限中适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,求这个圆形磁场区域的最小半径.(重力忽略不计).
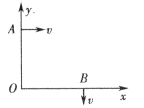
解析:
因为电荷有正、负两种可能性,磁场也有垂直于纸面向外和向里两种可能性,所以粒子从A到B也有两种可能的绕行方向.
(1)当粒子沿顺时针方向绕行时,偏转角为90°,即质点在磁场中运动的轨迹为圆周的1/4,射入方向与射出方向均应与圆周(虚线所示)相切,过这两个切点M、N作入射和出射方向的垂线,其交点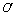 即为圆心(如图所示)该粒子在磁场内的运动轨迹就是以 即为圆心(如图所示)该粒子在磁场内的运动轨迹就是以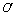 为圆心、 为圆心、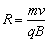 为半径的一段圆弧MN(虚线所示),在通过M、N两点所在圆周中,以MN为直径的圆周最小,所以磁场的最小半径为 为半径的一段圆弧MN(虚线所示),在通过M、N两点所在圆周中,以MN为直径的圆周最小,所以磁场的最小半径为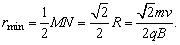
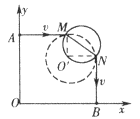
(2)当粒子沿逆时针方向绕行时,偏转角为270°,如图所示.因为M、N两点应位于磁场的边界上,MN弧必须在磁场内,所以最小半径就是弧MN的半径,即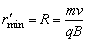 .因为 .因为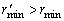 ,所以磁场的最小半径为 ,所以磁场的最小半径为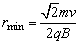 . .

- 返回 -
|