|
一、复习策略
动量变化量的计算
一条直线上的动量变化量的计算
一条直线上的动量变化量的计算分以下两种情况:
物体沿一条直线运动,方向不变:
选速度方向为正方向,有: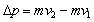
当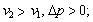
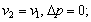
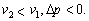
二、典型剖析
例1、质量为2kg的物体从静止开始以5m/s2加速度做匀加速直线运动,10s后撤去外力,物体做匀速直线运动,又经5s,物体开始做减速运动直到停止.分别求出各运动过程中的动量变化量.
解析:
设加速度的方向为正方向,在加速运动中有: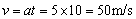
动量变化量为: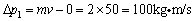
匀速运动中,速度不变,动量不变,故有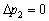
减速运动中,初速度为v,末速度为零.
则有: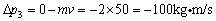
②物体在一条直线运动,方向改变:
设初速度的方向为正方向,则有: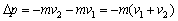
例2、质量为2kg的球,以5m/s的速度垂直撞击墙面,又以3m/s的速度反弹回来,试求此过程中球的动量变化量.
解析:设初速度的方向为正方向,则有:
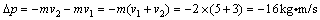
1、曲线运动中的动量变化量的计算
例3、质量为2kg的小球,在水平面内,以10m/s的速率作半径为10cm的匀速圆周运动,如图所示,试求小球在AB、AC、AD过程中的动量变化量.
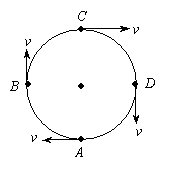
解析:在AB过程中,作矢量三角形如图①
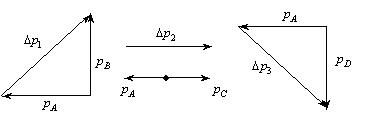
① ② ③
∵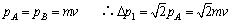
方向与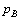 成45°角. 成45°角.
在AC过程中,设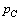 方向为正方向,如图②所示,则有: 方向为正方向,如图②所示,则有:
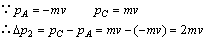
方向与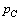 方向相同. 方向相同.
在AD过程中,作矢量三角形如图③所示,则有:
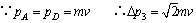
方向与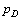 成45°角. 成45°角.
2、动量守恒定律解题技巧
应用动量守恒定律解题的步聚:
(1)确定研究对象——系统;
(2)分析系统受力情况,判断是否符合动量守恒定律的条件;
(3)确定相互作用的始、末时刻及相应的动量;
(4)选正方向,以确定各动量的正负;
(5)分析始、末状态,由动量守恒定律列方程;
(6)求解并检验.
例4、A、B两船及船上的货物的质量和分别为1000kg和2000kg,A、B两船分别以2m/s与3m/s的速率分别向东与向西方向行驶,当两船头尾相齐时,同时交换50kg的货物,交换货物时货物的移动方向与船速度垂直,求交换货物后两船的速度各多大?
解析:
以甲船余下部分与乙船的50kg货物为系统,向东为正方向,则由动量守恒定律得:
∴ 950×2-50×3=1000v1
故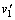 =1.75m/s,方向向东. =1.75m/s,方向向东.
以乙船余下部分与甲船的50kg的货物为系统,向西为正方向,由动量守恒定律得:
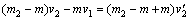
∴ 1950×3-50×2=2000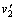
故 = 2.975m/s,方向向西. = 2.975m/s,方向向西.
说明:
如何巧选动量守恒的系统,对运用动量守恒定律是极为重要的,本题的选择方法,使系统内的两部分在作用以后具有相同的速度,只有一个未知量,这样可直接运用方程求解.动量是矢量,在运用动量守恒定律时.对同一个系统内的两个部分,必须以同一个方向为正方向,如第一个方向以向东为正方向,但对两个系统却不要求以同一方向为正方向,如第二个方向以向西为正方向。
3、弹性碰撞问题的分析方法
弹性碰撞指碰撞过程中不但系统的总动量守恒,而且碰撞前后的动能相等.
如两个物体弹性碰撞前的速度分别为v1、v2,弹性碰撞后的速度分别为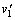 、 、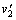 ,则有: ,则有:
动量守恒: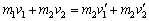 ① ①
动能相等: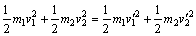 ② ②
由①②两式得: ③ ③
由①、③两式可以非常方便地求出碰后两物体的速度.
例5、如图所示,质量为m1的小球1从光滑曲线滑下,进入水平面后与质量为m2的小球2弹性正碰.碰后它们的落点到离水平面边缘的水平距离分别为s1和s2.试就(1)s1︰s2=1︰2;(2)s1︰s2=1︰3;(3)s1︰s2=3︰1;讨论m1与m2的关系.
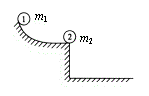
解析:
设小球1碰前的速度为v0,碰后小球1、2的速度分别为v1、v2.碰撞前后系统的总动量守恒,且总动能相等,则有:
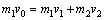 ① ①
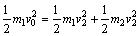 ② ②
由①②两式得: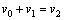 ③ ③
由①③两式得: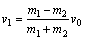 ④ ④
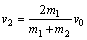 ⑤ ⑤
讨论:
设v0方向为正方向,则v2>0.若m1>m2,则v1>0.比较④⑤两式可知: 。 。
若 即质量相等的两物体发生弹性碰撞后,它们的速度交换. 即质量相等的两物体发生弹性碰撞后,它们的速度交换.
若m1<m2,则v1<0,即小球1反弹,比较|v1|与v2的大小.
若|v1|=v2,可得: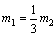
若|v1|>v2,可得: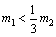
若|v1|<v2,可得: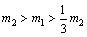
综上所述,本题碰后两球的速度关系取决于它的质量关系,其中m1=m2时两球速度交换是个界限,它决定着v1的方向为正还是为负.只有当m1<m2时,入射小球1反弹,它的速度大小才有|v1|≥v2的可能.这里决定|v1|与v2大小的界限是
有了上述清晰的图景,再分析本题就有了依据.由于两球都将从平台上作平抛运动,它们落地所用的时间相同,故两球位移大小之比为|v1|︰v2.
(1)当s1︰s2 =1︰2,表明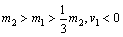
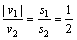 即: 即: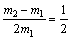 ∴m1︰m2=1︰2 ∴m1︰m2=1︰2
(2)当s1︰s2 =1︰3,有两种可能:
当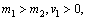 有: 有: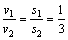 即: 即: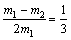
∴m1︰m2=3︰1
当 有: 有: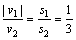 即: 即: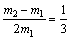
∴ m1︰m2=3︰5
(3)当s1︰s2 =3︰1时,只能是m1<m2,且v1<0,有: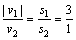
即: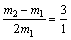 ∴ m1︰m2=1︰5. ∴ m1︰m2=1︰5.
4、求变力做功的几种方法
(1)将变力做功转化为恒力做功
我们知道变力做功不能直接用公式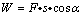 来计算,但在某些特殊情况下,将变力做功转换成恒力做功,就可以用求功公式直接求解. 来计算,但在某些特殊情况下,将变力做功转换成恒力做功,就可以用求功公式直接求解.
例6、如图所示,某人用大小不变的力F拉着放在光滑平面上的物体,开始时与物体相连的绳和水平面间的夹角是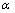 ,当拉力F作用一段时间后,绳与水平面间的夹角为 ,当拉力F作用一段时间后,绳与水平面间的夹角为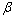 ,已知图中滑轮顶部的高度是h,求绳的拉力T对物体做的功,假定绳的质量,滑轮的质量与滑轮间的摩擦不计. ,已知图中滑轮顶部的高度是h,求绳的拉力T对物体做的功,假定绳的质量,滑轮的质量与滑轮间的摩擦不计.
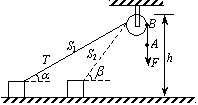
解析:
设绳对物体的拉力为T,显然人对绳的拉力F等于T,由于T在对物体做功的过程中,大小不变,但T的方向时刻在改变,因此上述问题是个变力做功问题.但在绳的质量、滑轮的质量及滑轮与绳的摩擦不计的情况下,人对绳的拉力F对绳做的功就等于绳的拉力T对物体做的功.而F的大小与方向都不变,因此,只要计算恒力F对绳做的功,就能解决问题.
设绳的拉力T对物体做的功为WT,人的拉力F对绳做的功为WF,由图可知,在绳与水平夹角由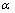 变到 变到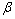 的过程中,拉力F的作用点的位移大小为: 的过程中,拉力F的作用点的位移大小为: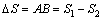
由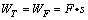 可知: 可知:
 . .
(2)用动能定理求解变力所做的功
如果我们所要研究的对象所受的一个或几个力中,只有一个变力,而其余都是恒力,而且这些恒力的功比较容易计算,研究对象本身的动能增量也较容易计算时,用动能定理就可以求出这个变力所做的功.
例7、质量m=1kg的物体,从轨道的A点由静止下滑,轨道AB是弯曲的,且A点高出B点h=0.8m,如图所示.如果物体在B点的速度为2m/s,求物体在轨道AB上克服摩擦力所做的功.
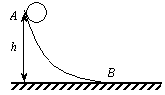
解析:
物体由A到B过程中,共受三个力作用:重力mg、支持力N、摩擦力f,由于轨道是弯曲的,轨道对物体的支持力是一个变力,摩擦力也是一个变力,但支持力N不做功.只有重力和摩擦力做功,由动能定理得:
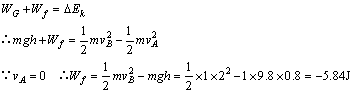
故物体在轨道上滑下时克服摩擦阻力所做的功为5.84J.
(3)用机械能守恒定律求变力做的功
如果物体只受重力和弹力作用,或只有重力和弹力做功时,则W外是重力和弹力做功的总和,动能定理就转化成机械能守恒定律.如果重力和弹力中有一个力是变力时,要求这个变力做的功,则可用机械能守恒定律求解.
例8、如图所示,质量为m=2kg的小球系在轻弹簧的一端,另一端固定在悬点O处,将弹簧拉至水平位置A,使弹簧无形变由静止释放,小球到达距O点下方h=0.5m处的B点的速度为2m/s.求小球从A到B的过程中弹簧弹力做的功.
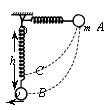
解析:
小球在运动过程中,只受重力和弹力作用,故系统机械能守恒.以B点为重力势能零势面,A点为弹性势能零势面,则在初态A有:
对末态B有: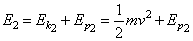
由机械能守恒定律得:E1=E2
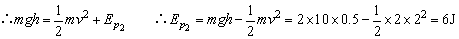
因弹性势能增加,故弹力做负功.
因此,小球从A到B的过程中,弹簧弹力做的功为-6J.
(4)用功能原理求变力所做的功
功能原理的内容是:系统所受的外力和内力(除重力、弹力外)所做的功的代数和等于系统的机械能的增量.如果这些力中,只有一个变力做功,就可用功能原理求变力所做的功.
例9、一辆车通过一根跨过定滑轮的绳子PQ提升井中质量为m的物体,如图所示.绳的P端拴在车的挂钩上,Q端拴在物体上,设绳的伸长、绳的质量、定滑轮的质量、滑轮上的摩擦忽略不计.开始时车在A点,左、右两侧绳都已绷紧,并且是竖直的,左侧绳长为H,提升时,车加速向左运动,沿水平方向从A经过B驶向C.设A到B的距离也为H,车在B点时的速度为vB,求车由A到B的过程中,Q端绳子的拉力对物体所做的功.
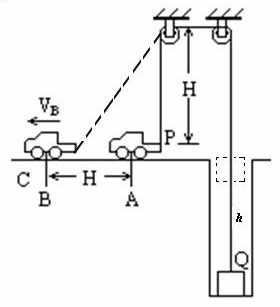
解析:
Q端绳子对物体的拉力等于汽车对P端绳子的拉力,这个力是变力,故本题是变力做功问题,可用功能原理求解.
设绳的P端到达B处时,左边绳与水平地面所成的夹角为θ,物体从井底上升的高度为h,速度为v,所求的功为W,则由功能原理有: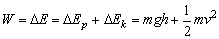
因绳的总长不变,故有: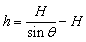
沿车速vB分解成垂直于绳的速度v1和沿绳的方向的速度v2,则有: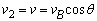
又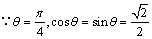 即 即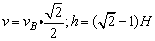
故有: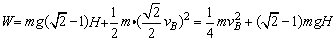
故Q端绳子对物体做的功为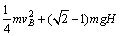
(5)利用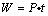 求变力所做的功 求变力所做的功
例10、一辆汽车的质量为105kg,该车从静止开始以恒定功率行驶,经过40s,前进40m,速度达到最大值.如果车受的阻力始终是车重的0.05倍,问车的最大速度是多少?
解析:
汽车在运动过程中,功率恒定,速度增加,所以牵引力不断减小,当减小到与阻力相等时速度达到最大值.汽车所受阻力是恒力,牵引力是变力.牵引力做功不能直接用公式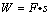 来求解,但可用公式W=P·t来求解.因为汽车达到最大速度时牵引力等于阻力,故有: 来求解,但可用公式W=P·t来求解.因为汽车达到最大速度时牵引力等于阻力,故有: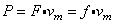
牵引力的功为: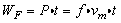
设阻力f做的功为Wf,由动能定理得: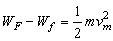

即: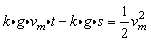
将: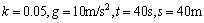 代入上式得: 代入上式得:
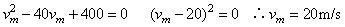
故此汽车的最大速度为20m/s.
(6)用数列求和公式求变力所做的功
例11、把一根长木桩打入泥土中,已知木桩在泥土中遇到的阻力与木桩进入泥土中的深度成正比,比例系数为k.把木桩等分成n段,将第一段打入泥土中时,给予木桩的能量为E,求把木桩的第n段打入泥土中和将整个木桩打入泥土中时,给予木桩的能量分别是多少?
解析:
木桩所受阻力f与木桩进入泥土中的深度x之间的关系为: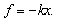
在把木桩打入泥土中时,要克服泥土的阻力做功,而阻力f是变力,因此本题属于变力做功的问题.
只要知道了木桩克服阻力做了多少功,由动能定理就可以知道需要给予木桩的能量.下面我们就用等差数列求和公式来求阻力f在木桩进入泥土过程中所做的功.
函数f =-kx的图象如图所示,图中OA同x轴及f轴的平行线所围成的面积就是阻力f所做的功.
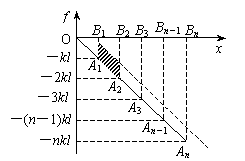
设木桩全长为nL,木桩n段进入泥土过程中,阻力f所做的功可分别用△OA1B1的面积S1、梯形B1A1A2B2的面积S2、梯形B2A2A3B3的面积S3……梯形Bn-1An-1AnBn的面积Sn来表示.
从图中不难看出:S1、S2、S3……Sn的大小是一个等差数列,其公差为:
d=平行四边形B1A1A2C的的面积,而△OA1B1的面积是将木桩的第一段打入泥土中时阻力所做的功,显然这个功是负值,故有:
由等差数列的通项公式 可知,将木桩的第n段打入泥土中阻力f所做的功为: 可知,将木桩的第n段打入泥土中阻力f所做的功为: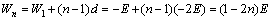
故将木桩的第n段打入泥土中必须给予木桩的能量为: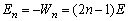
再由数列求和公式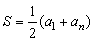 可知,将木桩全部打入泥土中阻力所做的功为: 可知,将木桩全部打入泥土中阻力所做的功为:
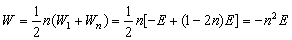
故将木桩全部打入泥土中必须给予木桩的总能量为: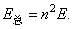
(7)用图象求变力所做的功
例12、用锤子把铁钉钉入木块中,设每次打击时,锤子给予铁钉的动能都相同,铁钉进入木块所受阻力跟钉入的深度成正比.如果钉子第一次被击入木块的深度为2cm,求第二次打击后可再进入的深度.
解析:
钉子进入木块所受的阻力f跟钉子进入木块的深度x间的大小关系为:f=kx
钉子得到锤子给予的动能,克服木块的阻力而做功,因阻力是变力,在钉子进入木块的过程中,阻力做功的过程是变力做功的问题.
作出f=kx的图象如图所示.第一次钉子克服阻力所做的功等于OA线下三角形的面积W1,第二次钉子克服阻力所做的功为AB线下面的梯形面积W2,因为每次打击时给予钉子动能都相等.故有W1=W2
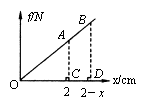
设第二次打击后,钉子再进入的深度为x,由图可知:△OAC∽△OBD
故由相似三角形的性质可知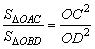
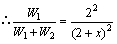 即: 即: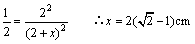
故在第二次打击后,钉子再进入木块的深度为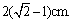
5、动能定理的应用
例13、总质量为M的列车,沿水平直线轨道匀速前进,其末节车厢质量为m,中途脱节,司机发觉时机车已行驶L的距离,于是立即关闭油门,撤去牵引力.设运动的阻力与重力成正比,机车的牵引力是恒定的.当列车的两部分都停止时,它们的距离是多少?
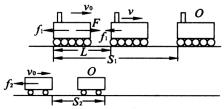
解析:
机车和车厢运动过程如图所示.对机车和车厢分别用动能定理得:
机车脱钩后全过程: ① ①
车厢脱钩后,有: ② ②
机车原来匀速行驶时有: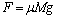 ③ ③
由图可知: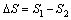 ④ ④
由①②③④式解得: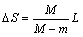
6、机械能守恒定律及其应用
例14、如图所示,质量为m1和m2的物体A、B通过定滑轮连接,A放在光滑水平面上,且m1>m2,B由静止开始下落.下落过程中绳始终拉紧,A在水平面上向右运动.当B下落h高度时,拉A的绳子与水平方向成θ角.若不计绳的质量和滑轮的摩擦.求此时B的速度.
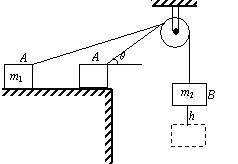
解析:
取A、B这个系统及地球—起为研究对象,在整个过程中只有重力对系统做功,所以系统的机械能守恒.
设B下落h时速度为v2,那么此时A的速度为: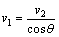 (想一想,为什么) (想一想,为什么)
由机械能守恒定律得: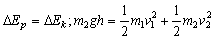
即: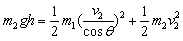
∴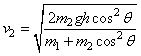
7、动量与能量综合问题的分析方法
例15、如图所示,在光滑水平地面上有一辆质量为M的小车,车上装有一个半径为R的光滑圆环.一个质量为m的小滑块从跟车面等高的平台以v0的初速度滑入圆环.试问:小滑块的初速度v0满足什么条件时,才能使它运动到环顶时恰好对环顶无压力?
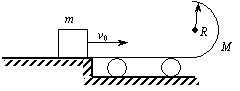
解析:
滑块滑到圆环的最高点恰对环顶无压力时,应有:
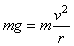 ① ①
式中v是滑块相对圆心O点的线速度,方向向左.
设小车此时的速度为v1,并以该速度为正方向,则滑块对地的速度为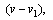 对滑块和小车组成的系统,由于水平方向所受合外力为零,由动量守恒定律得: 对滑块和小车组成的系统,由于水平方向所受合外力为零,由动量守恒定律得:
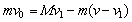 ② ②
由滑块和小车组成的系统机械能守恒得:
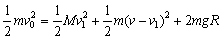 ③ ③
由①②③式联立解得:
说明:公式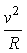 中的v是相对圆心O的线速度,而本题中的圆心是以v1向右运动的,所以滑块对地的速度为v-v1. 中的v是相对圆心O的线速度,而本题中的圆心是以v1向右运动的,所以滑块对地的速度为v-v1. - 返回 -
|