1、二倍角的正弦、余弦、正切
在和角公式S(α＋β)、C(α＋β)、T(α＋β)中，令α=β就可以得出对应的二倍角的三角函数公式．
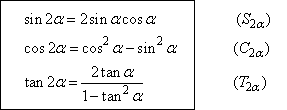
点拨：
（1）倍角公式是和角公式的特例．
（2）因为sin2α＋cos2α=1所以公式C2α还可变形为：
cos2α=2cos2α－1或 cos2α=1－2sin2α．
（3）公式成立的条件：C2α中α∈R；S2α中α∈R；T2α中α≠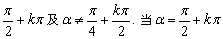
（k∈Z）时，显然tanα的值不存在，但tan2α的值是存在的，这时求tan2α的值可利用诱导公式，即：
．
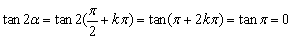（4）理解二倍角的含义：二倍角公式不仅可运用于将2α作为α的2倍的情况，还可以运用于诸于将4α作为2α的2倍，将α作为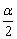
的2倍；将
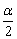作为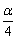
的2倍；将3α作为
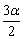的2倍；将
的2倍等等情况．
（5）注意公式的逆用：
例如：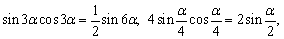
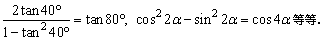
2、半角的正弦、余弦、正切
在倍角公式cos2α=1－2sin2α、cos2α=2cos2α－1中以α代替2α，以
代替α，即得：cosα=1－2sin2
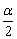，cosα=2cos2
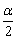－1，所以有
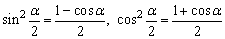即得：
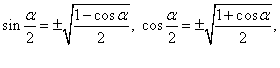
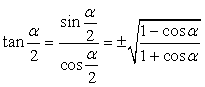称之为半角公式．
点拨：
（1）半角公式中正、负号的选取由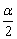
所在象限确定．
（2）称公式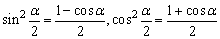
为降幂公式．
（3）
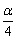可看做
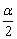的半角；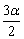
可看做3α的半角；
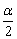可看做α的半角；2α可看做4α的半角等等．
（4）公式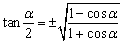
成立的条件为：α≠2kπ＋π(k∈Z)．
（5）
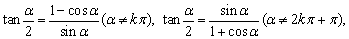k∈Z．
说明：半角公式不要求记忆．
3、积化和差与和差化积公式
将公式S（α＋β）加上S（α－β）即可得：
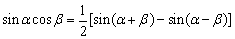，另外将公式S（α＋β）减去S（α－β）、C（α＋β）加上C（α－β）、C（α＋β）减去C（α－β）可得出另三个公式，即得积化和差公式如下：
在上述公式中令α＋β=θ，α－β=φ可得以下和差化积公式：
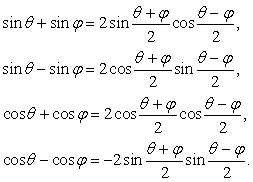
点拨：
（1）积化和差公式的推导，用了“解方程组”的思想，和差化积公式的推导用了“换元”的思想．
（2）正确地运用积化和差与和差化积公式的关键在于对式子的深刻观察：①观察角度的和差特点；②观察式子的整体结构特点．
说明：积化和差与和差化积公式不要求记忆．
，求sinα，cosα，tanα的值．
．
．
的值.