|
一、一周知识概述
本周学习了正弦、余弦的五组诱导公式及其简单应用——化简、求值.并对“任意角的三角函数”这一部分内容进行了检测和讲评.
二、重点知识讲解
1、正、余弦的诱导公式
公式一:sin(α+k·360°)=sinα
cos(α+k·360°)=cosα(k∈Z)
公式二:sin(180°+α)=-sinα
cos(180°+α)=-cosα
公式三:sin(-α)=-sinα
cos(-α)=cosα
公式四:sin(180°-α)=sinα
cos(180°-α)=-cosα
公式五:sin(360°-α)=-sinα
cos(360°-α)=cosα
总结:
α+k·360°(k∈Z),-α,180°±α,360°-α的三角函数,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
注:正切等其余的函数的诱导公式可通过同角三角函数关系式推导出。
2、诱导公式的推导
诱导公式二、三可由单位圆中的三角函数线来导出,即寻求180°+α(或-α)与α的同名三角函数值之间的关系,公式四、五可由公式一、二、三推导.
由五组诱导公式,可将任意角的三角函数值转化为0°~90°的三角函数值,从而利用数学用表查值.
利用诱导公式可以把任意角的三角函数转化为锐角三角函数,即:

例1、推导出180°+α,-α,180°-α,360°-α的正切、余切的诱导公式.
精析:
借助公式二、三、四、五和同角三角函数关系式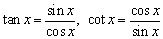 推导. 推导.
解答:过程略.
tan(180°+α)=tanα,cot(180°+α)=cotα
tan(-α)=-tanα,cot(-α)=-cotα
tan(180°-α)=-tanα,cot(-α)=-cotα
tan(360°-α)=-tanα,cot(360°-α)=-cotα
小结:
“函数名不变,正负看象限”不仅对于公式一~五成立,对于正切、余切函数也都成立,应深刻理解其含义.
2、诱导公式的应用——化简、求值、证明.
例2、设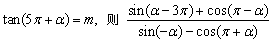 的值为( ) 的值为( )
A.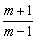 B. B.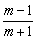
C.-1 D.1
精析:
利用诱导公式将条件等式和欲求式都化到α的同名三角函数上去,再利用同角三角函数基本关系式求解.
解答:
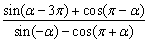 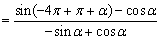
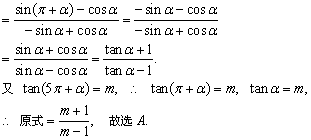
答案:A
例3、计算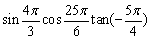 =____________. =____________.
精析:
诱导公式的一个重要作用就是将任意角的三角函数转化为锐角三角函数,于是可着眼于角的变换,并辅以特殊角的三角函数值求解.
解答: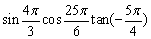
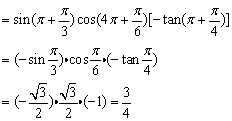
例4、已知A、B、C为△ABC的三个内角,求证:
(1)cos(2A+B+C)=-cosA;
(2)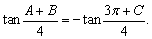
精析:
△ABC的三内角应满足A+B+C=π,注意到左右两边角的差异,利用诱导公式可证.
解答:
∵ A、B、C是△ABC的三个内角,∴ A+B+C=π.
(1)cos(2A+B+C)=cos(π+A)=-cosA;
(2)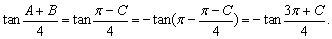
三、难点知识解析
灵活运用诱导公式对含n的式子的讨论等是本节内容的难点.
例5、已知函数f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β都是非零实数,且满足f(1997)=-1,则f(1998)=( )
A.-1 B.0
C.1 D.2
精析:
利用诱导公式寻求f(1998)与f(1997)的关系,并注意1998π=1997π+π的数量关系.
解答:
f(1997)=asin(1997π+α)+bcos(1997π+β)=-asinα-bcosβ,
f(1998)=asin(1998π+α)+bcos(1998π+β)=asinα+bcosβ,
两式相加,有f(1997)+f(1998)=0,
∴ f(1998)=1,故选C.
答案:C
例6、若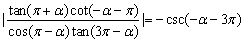 ,则α的取值范围是__________. ,则α的取值范围是__________.
精析:
采取逆向思维的方法,先用诱导公式和同角基本关系式将式子化简,再对比左右两边,得出α的取值范围.
解答:
原式变形为
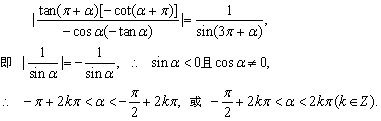
例7、化简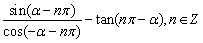 . .
精析:
为能应用诱导公式,需对整数n的奇偶性进行讨论.
解答:
当n为偶数时,设n=2k(k∈Z),
原式=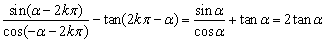 ; ;
当n为奇数时,设n=2k+1(k∈Z),
原式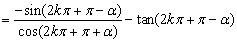
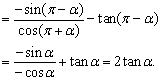
故原式=2tanα.
例8、化简
(1)tan1°·tan2°·tan3°·…·tan88°·tan89°
(2)2-sin221°-cos221°+sin417°+sin217°cos217°+cos217°
精析:
对90°的偶数倍的诱导公式应能熟练掌握和运用,而对于90°的奇数倍的诱导公式若能加以探索和掌握,则更能在解题时得心应手.
解答:
(1)∵ tanα=cot(90°-α),且tanα·cotα=1
∴ 原式
=tan1°·tan2°·tan3°·…·tan44°·tan45°·cot44°·…
·cot1°
=1·1·…·tan45°=tan45°=1
(2)原式
=2-(sin221°+cos221°)+sin217°(sin217°+cos217°)+cos217°
=2-1+sin217°+cos217°=2
|