|
一、一周知识概述
本周学习两个重要的概念:冲量和动量及一个重要的定理:动量定理。理解和掌握冲量的概念,知道冲量与力的区别,会求合力的冲量。理解和掌握动量的概念,知道动量与速度的区别,知道动量的运算服从平行四边形法则,会求动量的变化。能从牛顿运动定律和运动学公式推导出动量定理表达式,理解和掌握动量定理,知道动量定理的适用范围,并会用动量定理进行计算和解释现象。
二、重、难点知识归纳及讲解
(一)、冲量(I)
1、物理意义:表示物体在力的作用下经过一段时间累积的物理量。
2、定义:力F与力的作用时间t的乘积,叫做力F的冲量。
3、定义式:I=F·t.
4、冲量是矢量,方向由力的方向决定,与方向不变的力的方向相同。
5、单位:牛顿·秒(N·s)
6、冲量与力的比较
相同点:都是矢量,服从矢量的运算法则。
不同点:力具有瞬时性,其效果是产生加速度;冲量是过程量,力必须有一定的时间积累,其作用效果是改变物体的动量。
7、合力的冲量
(1)t相同,先求F合,再求I合=F合t.
(2)t不相同,先求各分力的冲量F1t1、F2t2……等,再求合冲量。
(二)、动量(p)
1、物理意义:动力学中描述物体运动状态的物理量,是状态量,具有相对性和瞬时性。
2、定义:物体的质量m和速度v的乘积mv,叫动量。
3、公式:p=mv
4、单位:千克·米/秒(kg·m/s)
5、动量是矢量,方向与速度的方向相同。
注:尽管1kg·m/s=1N·s,但冲量的单位必须用牛顿·秒,动量的单位必须用千克·米/秒。
6、动量与速度的区别
动量是动力学中反映物体运动状态的物理量,由m与v乘积决定,速度是运动学中反映物体运动状态的物理量,仅由v决定。
7、动量的变化(△p)
(1)末动量p与初动量p0的矢量差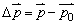 叫物体动量的变化。 叫物体动量的变化。
(2)在一条直线上:△p=mv-mv。(选取一个正方向)。
不在一条直线上:由矢量运算法则求解。
如图:可由矢量三角形求△p.

(3)动量的变化△p是对应一物理过程的过程量,它的大小和方向由过程初、末状态动量的矢量差决定,不能由某一时刻的动量大小和方向决定。(可比较v与△v的差别)
(三)、动量定理
1、动量定理的内容:物体所受合外力的冲量等于物体动量的变化。
2、表达式:I合=△p=p-p0.
F合t=mv-mv0.
或F1t1+F2t2+…+Fntn=mv-mv0.
3、对动量定理的理解
(1)动量定理反映了合外力的冲量是物体动量变化的原因。
(2)动量定理是矢量方程,研究的对象一般是单个物体。
(3)动量定理的适用范围:可以是恒力也可以是变力;宏观低速运动的物体,或微观现象高速运动的粒子。
4、动量定理与牛顿第二定律
动量定理的表达式变形可以得到牛顿第二定律另一种表达式:
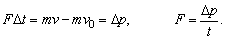
牛顿第二定律反映的是力与状态变化的瞬时关系,而动量定理是冲量与状态变化的过程关系。对于只涉及初、末状态的问题和变力问题,用动量定理这时就显露出独到的优越性。
5、用动量定理定性解释某些物理现象
用动量定理定性解释某些物理现象一般可分为两大类:
(1)物体的动量变化量△p是一定的,由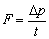 可知,作用时间越短,力就越大;反之作用力越小。 可知,作用时间越短,力就越大;反之作用力越小。
(2)作用力不变,由△p=Ft可知,作用力时间越长,动量变化越大。
用动量定理解释现实问题可以开阔思路,引发学生学习物理的成就感。
(四)、例题分析
平抛曲线运动中的动量、冲量问题
例1、将质量为m=1kg的小球,从距水平地面高h=5m处,以v0=10m/s的水平速度抛出;不计空气阻力,取g=10m/s2。求:
(1)平抛运动过程中小球动量的增量△p;
(2)小球落地时的动量p′;
(3)飞行过程中小球所受的合外力的冲量I。
分析:
作出示意图,水平方向v0不变,△vx=0;竖直方向自由落体.
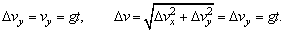
由速度合成可求v。
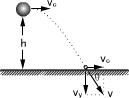
解:由平抛运动的竖直分运动为自由落体,有:

(1)因水平方向分运动为匀速直线运动,v0保持不变,所以其速度的增量 △v=△vy=vy=gt=10m/s
由 △p=△py=m△v-0=mvy=10kg·m/s.
(2)由速度合成,有:
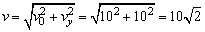 m/s m/s
所以小球落地时的动量大小为:
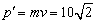 kg·m/s kg·m/s
p′的方向为: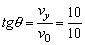 =1,与水平方向夹角为45°,斜向下方。 =1,与水平方向夹角为45°,斜向下方。
(3)小球飞行过程中只受重力作用,而重力mg是恒力,所以小球所受冲量为I=mgt=1×10×1=10N·s
方向竖直向下。
说明:此题考查动量、动量的增量和冲量等基本概念,以及矢量求和(合成)和用分运动研究曲线运动的方法。解题时要特别注意矢量性。
圆周运动中的动量和动量的增量问题
例2、质量为m=3kg的质点,以速度v=2m/s绕圆心O作匀速圆周运动,如图所示。
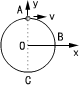
(1)小球由A到B转过1/4个圆周的过程中,动量变化量的大小为________,方向为________;
(2)若从A到C转过半个圆周的过程中,动量的增量的大小为_____,方向为_______,向心力的冲量I为________。
解析:
(1)如图所示,将vA移至B点,连两箭头末端得△v,解三角形,得:
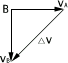
 kg·m/s kg·m/s
(2)如图所示,将vA移至C点,连两箭头末端得△v,由图知△v=vB+vA=2v,所以△p=m△v=12kg·m/s,方向沿-x方向。质点只受一个力的作用,此过程中向心力的冲量就是使质点动量变化的惟一原因,所以I=12kg·m/s。
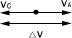
答案:
(1)△p=6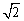 kg·m/s,θ=45°沿-x偏-y方向45°; kg·m/s,θ=45°沿-x偏-y方向45°;
(2)△p=12kg·m/s,沿-x方向,I=12kg·m/s.
说明:此题考查动量的增量,重点是矢量性及矢量运算方法。不在同一直线的两个矢量的和、差只能用几何方法求解。注意向心力的冲量不能用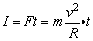 求解,因为 求解,因为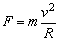 只是大小不变,它的方向随时变化,不是恒力。 只是大小不变,它的方向随时变化,不是恒力。
例3、质量为m=1.0kg的小球从h1=20m高处自由下落到水平地面上,反弹后上升的最大高度为h2=5.0m,小球与地面作用的平均时间为△t=0.1s.求在接触时间内,小球受到的平均作用力。
精析:
这是一个动量定理的问题。以小球为研究对象,小球受两个力的作用,即重力、地面对它的作用力。要解决这个问题,可选择不同的时间段用动量定理.
解法一:
分析小球受力如图所示,在小球与地面接触时间内运用动量定理
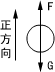
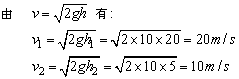
取向上为正方向,在△t=0.1s内列出动量定理方程:
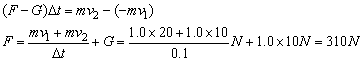
解法二:
在小球开始下落到小球弹回到5m高处的时间内用动量定理
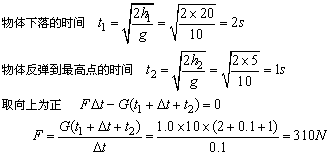
例4、据报道,1980年一架英国战斗机在威尔士上空与一只秃鹰相撞,飞机坠毁。小小的飞鸟撞坏庞大、坚实的飞机,真难以想象。试通过估计,说明鸟类对飞机的飞行的威胁,设飞鸟的质量m=1kg,飞机的飞行速度为v=800m/s,若两者相撞,试估算鸟对飞机的撞击力。
解析:
可认为碰撞前后飞机的速度不变,一直以800m/s的速度飞行,以飞机为参考系,以鸟为研究对象,由于撞击的作用很大,碰撞后可认为鸟同飞机一起运动,相对于飞机的末速度v′=0.设碰撞时鸟相对飞机的位移L=20cm(可认为是鸟的尺寸),则撞击的时间约为;

选飞机飞行的方向为正方向,根据动量定理得:

由①②两式解得鸟受的平均作用力:
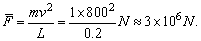
根据牛顿第三定律知,飞机受的撞击力的大小也为3×106N.
- 返回 -
|