（一）匀变速直线运动的规律的几个重要推论
1、速度位移关系式：vt2－v02=2as
根据匀变速直线运动的速度公式 vt=v0＋at和位移公式
，两式联立消去t即可得到速度位移关系式.在有些问题中，没有给出或者不涉及时间t，应用速度位移关系式解题比较方便。
2、某段时间内中间时刻的瞬时速度等于这段时间内的平均速度：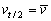
。
证明：由 vt=v0＋at可知，经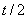
后的瞬时速度为：
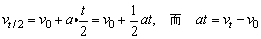
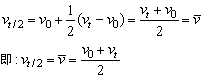
3、某段位移内中间位置的瞬时速度v中与这段位移的初、末速度的关系为：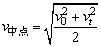
。
证明：
4、在连续相等的时间（T）内的位移之差为恒量：△s=aT2
证明：设物体以初速度 v0、加速度a做匀变速直线运动，
则自计时起时间T内的位移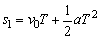
，
前2T时间内位移s2为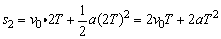
，
故第二个T内的位移SⅡ为：
SⅡ=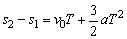
.
连续相等的相同内的位移差
。
即△ s=aT2.
对于任意两个连续的单位时间 T内如第(n－1)T内和第nT内的位移差可以这样讨论：由速度和位移公式有：
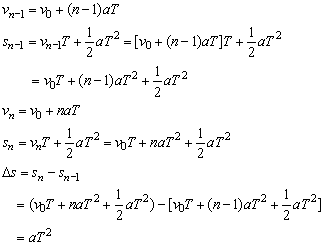
5、初速度为零的匀变速直线运动中，连续相等的时间T内的位移之比为奇数比.
s1︰s2︰s3︰…︰sn=1︰3︰5︰…︰(2n－1)
证明：
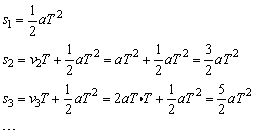
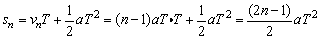
故 s1︰s2︰s3︰…︰sn=1︰3︰5︰…︰(2n－1)
6、初速度为零的匀变速直线运动中，物体通过连续相等的位移s所用时间比为：
t1︰t2︰t3︰…︰tn=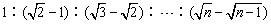
证明：
由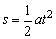
，有：
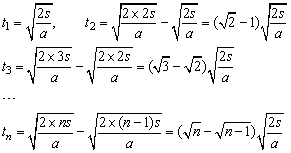
故 t1︰t2︰t3︰…︰tn=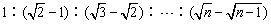
（二）学生实验：练习使用打点计时器和研究匀变速直线运动
1、实验原理
根据实验的目的：学会使用打点计时器和用打点计时器测匀变速物体的加速度。因此如何根据纸带求物体的加速度是本实验的重点。
物体做加速度为 a的匀加速直线运动，设任意连续相等的时间T内的位移分别为s1、s2、s3、…sn。则有：
△s=s2－s1=s3－s2=……=sn－sn－1=aT2
由此还可得到： s4－s1=s5－s2=s6－s3=3aT2
若在纸带上选六个计数点，则有：
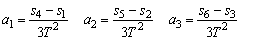
故物体的加速度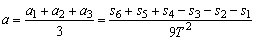
以上是运用逐差法求加速度的，我们还可以利用 v—t图象求物体的加速度。先由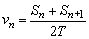
求出各点的瞬时速度，再作出v—t图象，图线的斜率即为物体运动的加速度。
2、注意事项
（1）应调整使细绳与木板平行，小车运动要平稳。
（2）选用合适的钩码，使小车的加速度适当大一些。
（3）操作时，应先接通电源，后释放小车。
（4）纸带上所选取的记数点不宜太少，不要分段测量各段位移，应一次性测量出各记数点到记数起点O之间的距离。读数时估读到毫米的下一位。
（5）处理纸带数据时，应注意：s1，s2，…，sn是连续相邻相等的时间内的位移，而不是各记数点到起点O的距离。
（三）例题
例 1、一个做匀加速直线运动的质点，在最初两个连续的4s时间内发生的位移分别为s1=24m和s2=64m，求质点运动的初速度和加速度。
解析：
解法
1 ：由于做匀变速直线运动的物体，在任意两个连续相等的时间间隔内的位移差为一常量：
△s=aT2 。据此可求加速度：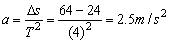 
设初速度为 v0 ，在最初 4s 内位移为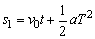
，经化简，可知初速度为：
解法 2 ：在最初的两个连续的 4s 时间内，质点的平均速度为：
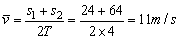
在第一个 4s 时间内，质点的平均速度为：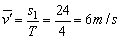 
由于做匀变速直线运动的物体在某段时间内的平均速度等于该段时间中间时刻的瞬时速度。
可见： 4s 末质点的瞬时速度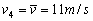 
，
2s
末的瞬时速度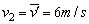 
，
则加速度为：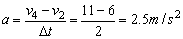 
；
由 vt=v0 ＋
at ，
可得： v0=vt－at=v2－2a=6-2×2.5=1m/s.
答案： v0=1m/s ， a=2.5m/s2.
例 2、一观察者站在列车第一节车厢的前端，列车从静止开始做匀加速运动。第一节车厢驶过他身边所用的时间为t1，设每节车厢等长。求第n节车厢驶过他身边需要多少时间？（车厢之间的距离不计）
解法
1 ：
设列车加速度为 a ，每节车厢长 L ，
以 t1 ， t2 ，…，
tn 为列车发生 1 个 L、 2 个 L、……、
n 个 L 的位移所需的时间，
则第一节车厢通过观察身边时，有：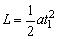
①
（n－1）节车厢通过观察身边时，有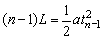
②
n节车厢通过观察身边时，有
③
则第 n节车厢通过观察者身边，即列车发生第n个位移所需时间为：
t=tn－tn－1 ④
由①②③④联立，解得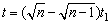
解法 2：
因为列车初速度为零，且做匀加速运动，如记t1、t2、…、tn为列车发生第1个L、第2个L、……、第n个L的位移所需的时间，则此等分位移的时间比为：
t1︰t2︰…︰tn=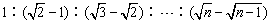
故△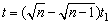
解法 3：
设第n节车厢通过观察者身边的初速度为vn－1，则：
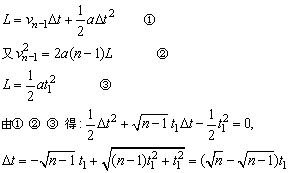
解法4：作出列车的速度—时间图象，如图所示，两块阴影面积相等，即：
。 
