|
一、一周知识概述
本周学习内容是高二下数学第九章的第五节,即§9.5空间向量及其运算,共用时六课时.具体安排为:空间向量及其加减与数乘运算用时1课时;共线向量及共面向量用时1课时;空间向量基本定理用时1课时,两个向量的数量积1课时,另两课时为这一节学习内容的综合习题课.
在本周的课本学习中,我们首先把平面向量及其线性运算推广到空间向量.在同学们已有了空间直线和平面平行,以及平面和平面平行的概念,这一推广对同学们来说应该不会感到太难,但我们仍要牢记,现在研究的范围已由平面扩大到空间.一个向量已是一个平移,两个不平行的向量确定的平面已不是一个平面,而是互相平行的平面集,其中我们可以通过在空间上一步步地验证运算法则和运算律,一方面通过学习空间向量复习了平面向量(高一学习的),另一方面培养了我们的空间观念.
当我们把平面向量推广到空间向量后,很自然地要认识空间向量的两个最基本的子空间:共线向量和共面向量,把平行向量基本定理和平面向量基本定理推广到空间,然后由这两个定理推出空间直线和平面的向量表达式.有了这两个表达式,我们就可很方便地使用向量工具解决空间的共线和共面问题.
在学习共线和共面向量定理后,我们学习空间最重要的基础定理:空间向量基本定理.这个定理是空间几何研究数量化的基础.有了这个定理空间结构变得简单明了,整个空间被三个不共面的基向量所确定.这样,空间的一个点或一个向量与实数组(x,y,z)建立起了一一对应关系.
最后,我们学习了本节的最后一个知识点——两个向量的数量积,将平面两个向量的数量积推广到空间,建立起了向量在轴上的投影的概念,并学习了内积的几个运算性质.
通过这一周的学习,同学们建立起了空间向量的概念,初步将空间向量与空间图形联系起来,并通过课堂内外的例、习题的讲解与学习,初步学会用向量知识来解决立体几何问题的方法与技巧.
二、重、难点知识的归纳与剖析
(一)本周学习与研究中的四个重点
1、空间向量的运算及运算律
空间向量加法,减法,数乘向量的意义及运算律与平面向量类似.学习过程中,我们要加强直观说理,结合式与图之间的互相转换加深理解.如:
(1)首尾相接的若干向量之和等于由起始向量的始点指向末尾向量的终点的向量.因此,求空间若干向量之和时,可通过平移将它们转化为首尾相接的向量;
(2)首尾相接的若干向量若构成一个封闭图形,则它们的和为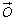 ; ;
(3)两个向量相加的平行四边形法则在空间仍成立.因此求始点相同的两个向量之和时,可考虑用平行四边形法则.
2、共线向量定理和共面向量定理
由于空间向量的平行(共线)的定义、共线向量定理等与平面向量完全相同,都是平面向量的相关知识向空间的推广,因此,我们可以在熟练地掌握平面向量这些知识的基础上来加深理解.其中要明确如下几点:
(1) 的两条有向线段所在直线既可能是同一直线,也可能是平行直线;当 的两条有向线段所在直线既可能是同一直线,也可能是平行直线;当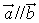 时,也具有同样的意义; 时,也具有同样的意义;
(2)运用确定平面的条件可以将空间向量问题转化为平面向量问题;
(3)理解共线向量定理时,应知道该定理包含两个命题:

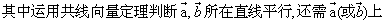 有一点不在 有一点不在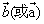 上; 上;
(4)空间直线的向量参数方程是空间共线向量定理的具体体现;

3、空间向量基本定理
空间向量基本定理与平面向量基本定理类似,区别仅在于基底中多了一个向量,从而分解结果中也多了一“项”,因此不难理解.空间向量基本定理说明了用空间三个不共面已知向量组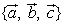 可以线性表示出空间任意一个向量,而且表示的结果是唯一的. 可以线性表示出空间任意一个向量,而且表示的结果是唯一的.
4、两个向量的数量积的计算方法及其应用.
理解两个向量的数量积的定义是利用两个向量的数量积开展计算的关键,其中还要结合它的一些性质.其具体应用是思考如下几个问题:
(1)如何把已知的几何条件转化为向量表示?
(2)考虑一些未知的向量能否用基向量或其它已知向量表示?
(3)如何对已经表示出来的向量进行运算,才能获得需要的结论?
(二)本周学习与研究中的难点
应用向量解决立体几何问题是贯穿于本节学习始终的一个难点.它涉及到如何利用向量的运算法则及定律将一些线线间的关系用向量刻画,然后利用共线向量定理,共面向量定理证明多点共线,多线共面问题,最后利用向量的数量积的定义及性质来解决有关求线段长,求异面直线所成的角的计算问题.突破该难点的方法可以采用多练习去实现,从练习中悟出其中的技巧和方法.
三、例题点评
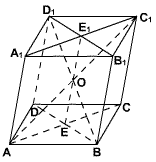
例1、如图中,已知点O是平行六面体ABCD-A1B1C1D1体对角线的交点,点P是任意一点,则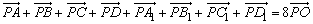 . .
分析:
将要证明等式的左边分解成两部分: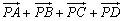 与 与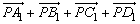 ,第一组向量和中各向量的终点构成平行四边形ABCD,第二组向量和中的各向量的终点构成平行四边形A1B1C1D1,于是我们就想到了应该先证明: ,第一组向量和中各向量的终点构成平行四边形ABCD,第二组向量和中的各向量的终点构成平行四边形A1B1C1D1,于是我们就想到了应该先证明:
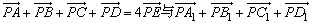 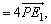
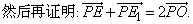 将以上所述结合起来就产生了本例的证明思路. 将以上所述结合起来就产生了本例的证明思路.
解答:
设E,E1分别是平行六面体的面ABCD与A1B1C1D1的中心,于是有
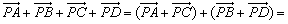 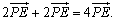

点评:
在平面向量中,我们证明过以下命题:已知点O是平行四边形ABCD对角线的交点,点P是平行四边形ABCD所在平面上任一点,则 ,本例题就是将平面向量的命题推广到空间来. ,本例题就是将平面向量的命题推广到空间来.
例2、已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.
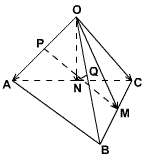
分析:欲证PM⊥QN,只要证明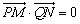
解答:
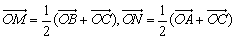

点评:
欲证 用相同的几个向量表示出来,然后利用向量的数量积. 用相同的几个向量表示出来,然后利用向量的数量积.
例3、如图,E是正方体ABCD-A1B1C1D1的棱C1D1中点,试求向量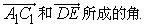
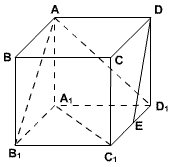
分析:
利用数量积定义,求出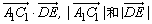 ,再求出所成角的余弦. ,再求出所成角的余弦.
解答:
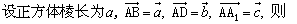

点评:
求向量 所成角,首先应将 所成角,首先应将 用一组基底表示出来,再利用公式 用一组基底表示出来,再利用公式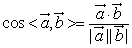 . .
|