本周学习如何建立空间直角坐标系，会用坐标来表示空间向量和空间中的点的位置关系，并会进行空间向量的坐标运算，利用坐标来研究平行向量，垂直向量间应满足的坐标关系，会求空间两点间的距离，两向量间的夹角．
空间向量的坐标运算关键是建立恰当的坐标系，因为它虽不影响线线、线面、面面位置关系的确定，但它对坐标的影响很大，更对计算的繁简有很大影响.
空间向量的坐标运算类似于平面向量的坐标运算，为解决立体几何问题提供有力的工具：夹角公式可求解立体几何中“线线”“线面”成角问题；空间两点间距离公式可计算空间线段的长度；利用向量的平行与垂直证明线线平行、线线垂直等问题带来了方便.
（一）本周学习与研究中的三个重点
1、空间右手直角坐标系及其在空间右手直角坐标系下的向量坐标运算．
空间直角坐标系是在仿射坐标系的基础上，选取空间任意一点O和一个单位正交基底{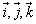
}（
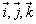按右手系排列）建立的坐标系．具体选择坐标系时，注意O点的任意性，一方面既要有利于作图的直观性，另一方面又要注意有关要求点的坐标容易表示．
在空间右手直角坐标系下的点，向量坐标是唯一的，这一点的理解和证明可仿照向量分解定理的唯一性理解和证明．由此说明相等的向量其坐标是唯一的，这为后面的解题中常常需要进行向量的平移提供理论依据．
空间向量的坐标运算，加法、减法和数量积等与平面向量类似，具有类似的运算法则，同学们学习中可类比的学习．虽然一个向量在不同空间的表达方式不同，但其实质没变，即向量
在平面上是用唯一确定的有序实数对表示，即
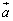=(x,y)，而在空间则用唯一确定的有序实数组表示，即
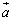=(x,y,z)．如向量的数量积
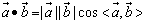在二维、三维空间都是这样定义的．不同点仅是向量在不同空间具有不同的表达形式．如在平面上,
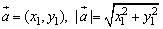,在空间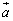
=(a1,a2,a3), 
，不论在平面或空间都有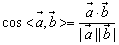
．
2、空间两向量平行、垂直的充要条件
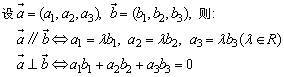
空间两向量平行时与平面两向量平行的表达式不一样，但实质是一致的，即对应坐标成比例，且比值为λ，空间两向量垂直的充要条件形式与平面向量里类似，仅多了一项基向量而已．
3、空间两向量的夹角公式，距离公式，中点坐标公式
（1）
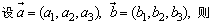
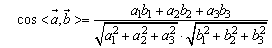
（2）
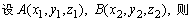
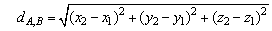
（3）
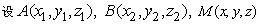为AB的中点，
则由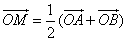
可知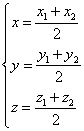
夹角公式在平面向量正文里没有涉及，但可根据数量积的定义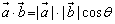
推出．这里应注意两向量夹角范围是：0°≤θ≤180°，当θ=0°时，表示两向量为同向共线向量，当θ=90°时，表示两向量垂直，当θ=180°时，表示两向量为反向共线向量．
两点间的距离公式是长度公式的推广．其推导过程是首先根据向量的减法，推出向量
的坐标表示，然后再用长度公式推出．
这几个公式都与坐标原点的选取无关．
（二）本周学习与研究中的两个难点
1、空间任意一点的坐标确定
空间任一点P的坐标确定办法如下：过P分别作三个坐标平面的平行平面（或垂面），分别交坐标轴于A、B、C三点，|x|=OA，|y|=OB，|z|=OC，当
方向相同时，x>0，反之x<0，同理，可确定y、z．具体理解，可以以长方体作为模型，以其一共点的三条棱，建立空间直角坐标系来理解．
这其中同学们应准确判断一点在各坐标平面内的射影的坐标，并比较它们间的关系，以及一些特殊点，如落在坐标轴上的点的坐标形式等．
2、距离公式，夹角公式的应用
应用距离公式、夹角公式解决立体几何问题，关键在于选择建立适当的空间直角坐标系．它们在立体几何中的应用有：计算两异面直线所成角时，当用几何方法较困难时，可以建立适当的空间直角坐标系后，利用向量方法求解，此时应注意异面直线所成的角的范围与向量夹角范围的区别；求线段的长度时，有时用几何方法较难构造三角形，此时，可考虑应用向量方法，表示出线段两端点的坐标，然后再用两点间的距离加以解决．
试问是否存在实数λ，μ，v.
如果存在，算出λ，μ，ν，如果不存在，请给出证明．