|
一、一周知识概述
本周主要学习高二下数学第九章的第5节,两个平面平行的判定和性质.
在本周的学习中,共有两个知识点:两个平面平行的判定定理,两个平面平行的性质定理.通过本周的学习,要理解平面与平面平行与相交两种位置关系,面面平行的判定和性质.
二、重、难点知识讲解
重点:两个平面平行的判定定理和性质定理;
难点:证明两个平面平行的判定定理的方法;
疑点:证明两个平面平行的判定定理时怎样用反证法思想
(一)平面与平面平行的判定定理
如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
由此我们可以得到如下推论:如果一个平面内有两条相交直线都平行于另一个平面内的两条直线,那么这两个平面平行.
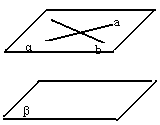
定理中的条件缺一不可,用符号语言表示为: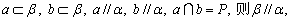 两个平面平行问题的判定或证明,是将其转化为一个平面内的直线与另一个平面平行的问题,即“线面平行,则面面平行”,必须注意这里的“线面”是指一个平面内的两条相交直线和另一个平面. 两个平面平行问题的判定或证明,是将其转化为一个平面内的直线与另一个平面平行的问题,即“线面平行,则面面平行”,必须注意这里的“线面”是指一个平面内的两条相交直线和另一个平面.
两个平面平行的画法
图示:

(二)平面与平面平行的性质定理
如果两个平行平面都和第三个平面相交,那么它们的交线平行,由两个平面平行,我们还有:
1、如果两个平面平行,那么其中一个平面内的直线平行于另一个平面;
2、和两个平行平面同时垂直的直线,叫做这两个平行平面的公垂线。它夹在这两个平行平面间的部分叫这两个平行平面的公垂线段。公垂线段的长度叫做两个平行平面的距离。
注意:①两个平面平行,其中一个平面内的直线必平行于另一个平面.但这两个平面内的所有直线并不一定相互平行.它们可能是平行直线,也可能是异面直线,但不可能是相交直线.
②两个平面平行的性质定理指出两个平面平行时所具有的性质:如果两个平面平行同时与第三个平面相交,那么它们的交线平行.
③一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.
(三)线线平行,线面平行,面面平行的转化。
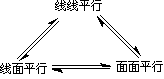
要理解这三者之间的联系,由相应的判定定理和性质定理将它们联结起来。
三、例题讲解
例1、α、β是两个不重合的平面,可判定平面α与平面β平行的是( )
A.α、β都垂直于平面γ
B.α内不共线的三点到平面β的距离都相等
C.l、m是平面α内两条直线,且l∥β,m∥β
D.l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
分析:
本题是属于基本概念类的问题,其实是下列哪个选项可以推证出α∥β.对于有的选项我们只要列举反例即可,也可以用淘汰法解选择题.
解:
考查四个选项:对于A,设直线c⊥平面γ,经过直线c作平面α和平面β,即α⊥γ且β⊥γ.但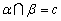 ,即α与β不平行,从而选项A不正确;对于B,条件极具有迷惑性,极易错误地判定B是对的.这是因为“α内不共线三点到β距离都相等”.易造成下列两个错觉,一是不共线三点可确定两条相交直线,二是由距离相等,极易认为相交线均平行于β.其实B中条件并没有指明三点在β的同一侧,也就是说明三点可能在β的两侧.虽然到β的距离都相等,但α与β仍是相交的.所以B也不正确;对于C,当α、β相交于直线c,并且l、m是α内都与c平行的直线,则有l∥m,但 ,即α与β不平行,从而选项A不正确;对于B,条件极具有迷惑性,极易错误地判定B是对的.这是因为“α内不共线三点到β距离都相等”.易造成下列两个错觉,一是不共线三点可确定两条相交直线,二是由距离相等,极易认为相交线均平行于β.其实B中条件并没有指明三点在β的同一侧,也就是说明三点可能在β的两侧.虽然到β的距离都相等,但α与β仍是相交的.所以B也不正确;对于C,当α、β相交于直线c,并且l、m是α内都与c平行的直线,则有l∥m,但 ,即α和β不平行.从而选项C也不正确;对于D,由于平行于两条异面直线的平面必垂直于这两条异面直线的公垂直线,所以α和β都垂直于异面直线l、m的公垂线,从而α和β平行.即D是正确的. ,即α和β不平行.从而选项C也不正确;对于D,由于平行于两条异面直线的平面必垂直于这两条异面直线的公垂直线,所以α和β都垂直于异面直线l、m的公垂线,从而α和β平行.即D是正确的.
例2、在棱长为a的正方体ABCD—A1B1C1D1中,设M,N,E,F分别是棱A1B1,A1D1,C1D1,B1C1的中点.
(1)求证:E、F、B、D四点共面.
(2)求证:面AMN∥平面EFBD.
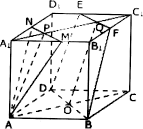
分析:
(1)要证四点共面,只须判断出 EF 所在直线与 BD 所在直线互相平行即可 .
(2)要证明面面平行,只须证明出线面平行即可.
解答:
(1)分别连结 B1D1,ED,FB,则由正方体性质得 B1D1∥BD ,
∵ E,F 分别是 D1C1和 B1C1的中点,
∴ EF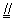 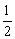 B1D1,∴ EF B1D1,∴ EF 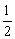 BD. BD.
∴ E ,F ,B ,D 四点共面.
(2)连结 A1C1交 MN 于 P 点,交 EF 于点 O ,
连结 AC 交 BD 于点 O ,分别连结 PA , QO.
∵ M 、 N 为 A1B1, A1D1的中点 .
∴ MN ∥ EF , EF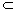 平面 EFDB. 平面 EFDB.
∴ MN ∥面 EFDB.
∵ PQ AO ,∴四边形 PAOQ 为平行四边形, AO ,∴四边形 PAOQ 为平行四边形,
∴ PA ∥ OQ.
而 OQ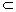 平面 EFBD ,∴ PA∥面 EFBD. 平面 EFBD ,∴ PA∥面 EFBD.
且 PA∩MN=P , PA , MN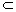 面 AMN. 面 AMN.
∴平面 AMN ∥平面 EFBD.
点评:
判定或证明两个平面平行的方法主要是利用两个平面平行的判定定理,将面面平行问题转化为线面平行,然后又将线面平行问题转化为线线平行问题,实现这之间的转化,具体如下:线线平行 线面平行 线面平行 面面平行 面面平行
例3、a和b是两条异面直线,求证:
(1)过a和b分别存在平面a、b,使a∥b;
(2)a和b的距离等于平面a和b的距离.
证明:(1)在直线a上任取点P,
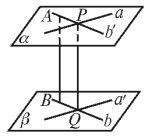
过P作b′∥b.
∵ a、b是异面直线,
∴ a、b′是相交直线.
设a、b′确定平面为α.
同理在b上任取一点Q,过Q点作a′∥a,a′、b是相交线.
a′,b可确定一个平面,设为β.
∵ a′∥a,a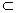 α,∴ a′∥α 同理b∥α. α,∴ a′∥α 同理b∥α.
又∵ a′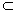 β,b β,b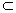 β,a′∩b=Q,∴ α∥β. β,a′∩b=Q,∴ α∥β.
因此分别存在过a和b的平面α、β,使α∥β.
(2)设AB是两条异面直线a和b的公垂线,
则AB⊥a,AB⊥b.
∵ a′∥a,AB⊥a′,
又a′和b是β内的相交直线,
∴ AB⊥β,同理AB⊥α.
因此,线段AB的长既是异面直线a和b的距离,又是平行平面α和β的距离.
所以异面直线a和b的距离等于两个平行平面a和b的距离.
点评:
(1)空间的两条异面直线分别存在于两个平行平面内.
(2)两条异面直线的距离等于两个平行平面的距离.因此:异面直线的距离也可转化为直线和平面的距离.
例4、ABCD为空间四边形,M、E、F分别为△BAC、△ACD及△ADB的重心.
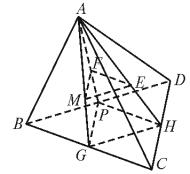
(1)求证:面MEF∥面BCD;
(2)求S△MEF与S△BCD面积比值.
解:
(1)证明:连AM、AE及AF,分别延长,使之交BC、CD、DB于G、H、P三点
因E、F、M分别为三角形的重心,
∴ 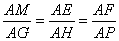 = =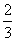
∴ 连ME、EF、FM及连GH、HP、PG后有
ME∥GH,EF∥PH,
即ME∥面BCD,EF∥面BCD.
故面EFM∥面BCD.
(2)解:由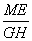 = =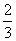 , ,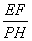 = =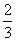 , ,
ME=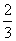 GH,EF= GH,EF=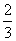 PH. PH.
而GH=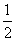 BD,PH= BD,PH=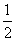 BC, BC,
故ME=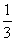 BD,EF= BD,EF=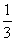 BC. BC.
即 = =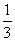 . .
则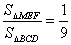 . .
点评:
题目的解决离不开平行平面判定及性质,但同时要求对基本性质,旧的知识点熟悉,清楚其在解题中作用.
|