|
一、一周知识概述
本周主要是学习了棱锥的有关知识和多面体欧拉定理的发现.要求掌握棱锥、正棱锥的概念及性质;会求棱锥的体积,能利用等积法求点面距离;掌握欧拉公式的内容及证明,会应用欧拉公式解决一些简单问题.
二、重难点讲解
1、棱锥的定义
棱锥的定义:如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥.
正棱锥的定义:如果一个棱锥的底面是正多边形,并且顶点在底面上的射影是底面的中心,这样的棱锥叫正棱锥.
2、棱锥的性质
如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比.
特别地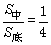 (S中指的是中截面面积) (S中指的是中截面面积)
正棱锥的性质
(1)正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).
(2)正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形;正棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形.

4、棱锥的体积
V锥=
利用三棱锥的体积求点面距离一般是通过等体积变换实现的,这往往是求点面距离的最佳选择.
例1、若正四棱锥底面边长为a,侧棱与底面成60°角,求正四棱锥的侧棱和斜高.
[解析]
例2、P是△ABC所在平面外的一点,PA,PB,PC两两垂直,PA=PB=PC=3,求P到平面ABC的距离.
[解析]
例3、已知S一ABCD是一个正四棱锥,延长CD到E,使DE=2CD,经过B、E和棱SC的中点F作一个平面,此平面把四棱锥分成两部分,求这两部分的体积之比.
[解析]
5、欧拉公式
(1)简单多面体的定义
表面经过连续变形可变为球面的多面体,叫做简单多面体.
一切凸多面体,如棱柱、棱锥、正多面体等均是简单多面体.不是凸多面体的多面体,可能是简单多面体,也可能不是.
(2)多面体欧拉定理
简单多面体的顶点数V,棱数E及面数F间有关系:
V+F-E=2.
①关系式V+F-E=2叫欧拉公式,又称为欧拉示性数.不同类型的多面体,它们的欧拉示性数也不同.
②在推导欧拉公式时,将复杂的不易想象的多面体的顶点数、面数、棱数的关系问题转化成我们熟知的、易掌握的平面图形的顶点数、面数、棱数的关系问题.这种空间问题平面化的转化思想应予以重视.
③欧拉公式可看成平面多边形的顶点数V,面数F,棱数E满足的关系式V+F-E=2的推广形式.
(3)对于简单多面体而言,V+F-E是一个常数,其棱数E有三种计算方法:(1)E=V+F-2;(2)E=各面多边形的边数之和的一半;(3)E=顶点数与共顶点的棱数之积的一半.
例4、已知单晶铜外形是简单多面体,单晶铜有三角形和八边形两种晶面,如果单晶铜有24个顶点,以每个顶点为一端都有三条棱,计算单晶铜的两种晶面的数目.
[解析]
例5、一个正多面体各个面的内角和为3600°,求它的面数、顶点数和棱数.
[解析]
|