|
一、一周知识概述
本周学习内容是高二下数学第九章的第四节,即§9.4直线和平面垂直,共用时四课时.具体安排为:直线和平面垂直的判定定理1课时,正射影和三垂线定理2课时,另一课时利用正射影及三垂线定理进行线线垂直,线面垂直间的互化的灵活运用的习题课.
在本周的课本学习中,我们首先解决了利用直线和平面垂直的定义直接判定线面垂直时要考虑平面内的每一条直线(由于平面内的直线有无数条)的困难,学习了直线与平面垂直的判定定理.根据这一定理,只要在平面内选择两条相交直线,考虑它们是否与平面外的直线垂直即可,这个定理将原本判定线面垂直的问题,转化为判定直线和直线垂直来解决,然后我们学习了正射影、平面的斜线、斜足、斜线段等概念.同学们在学习过程中要充分利用好教材上P23图9-39,借助这一图形来正确理解点、线、图形F在平面内的射影的概念,这样为学习三垂线定理及其逆定理等内容打好基础,最后利用直线和平面垂直的判定定理证明了三垂线定理及其逆定理,得到了一个证明线线垂直的好工具.在直线和平面垂直的判定定理、三垂线定理、三垂线定理的逆定理等定理的证明过程中,同学们将会体会到将空间几何问题转化成平面几何问题的这一学习立体几何的主要思想,并且通过课堂内、外的习题练习,熟悉并熟练掌握线线垂直与线面垂直的互相转化的方法与技巧.
二、重难点知识的归纳与剖析
(一)本周学习与研究中的两个重点
1、直线与平面垂直的判定定理
如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
关于定理的理解须注意如下几点:
(1)定理中的三个条件:两个线线垂直和一个相交条件推得结论.三个条件缺一不可,尤其是最后一个——两条相交直线这一条件极易忽视.如命题1:如果一条直线垂直于平面内的两条直线,那么这条直线垂直于这个平面;命题2:如果一条直线垂直于平面内的无数条直线,那么这条直线垂直于这个平面.以上两个命题都是错误的,因为对于这两个命题,都没有体现出两直线相交这一特性,无数条直线可以是一簇平行线,并不一定具备有两条相交直线和已知直线垂直,因此,也就不一定得出这一直线垂直于这个平面这一结论.
(2)要判定一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,这是无关紧要的.
(3)作用:直线和平面垂直的判定定理是判定直线和平面垂直的理论依据,它可以将要证线面垂直问题,转化成证线线垂直问题.
2、三垂线定理及其逆定理
(1)三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
(2)三垂线定理的逆定理:在平面内的一条直线,如果和这个平面内的一条斜线垂直,那么它也和这条斜线的射影垂直.
理解这两定理要抓住其中组成元素及关系.三垂线定理及其逆定理涉及到一个平面和四条直线,三个垂直关系,它们间的关系见下表:
| |
三垂线定理 |
三垂线定理的逆定理 |
条件 |
PA⊥α,AO为PO在α内的射影,a⊥AO,a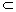 α α
|
PA⊥α,AO为PO在α内的射影,PO⊥α,a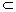 α α
|
结论 |
a⊥PO |
a⊥AO |
三垂线定理及其逆定理利用了平面的斜线和它在这个平面上的射影所确定的平面POA的垂线a与平面POA内所有直线垂直的关系,从而缩短了线线垂直与线面垂直的变化过程,它的实质是实现由线线的相交垂直证明线线的空间垂直,而逆定理恰恰相反.
这两个定理给我们提供了证明两线垂直的一种较好的方法,与同直线垂直平面则直线与平面内直线垂直一起作为我们立体几何中证明线线垂直的两种常用方法.
在应用三垂线定理及逆定理时,首先要恰当地选择平面与该平面的垂线,常常成为应用三垂线定理解决问题的关键,要注意图形位置的变化,摆脱思维定势,其次对“平面内一直线”要理解好,否则定理不一定成立.
最后活用三垂线定理及逆定理,既是重点,又是难点.
区别两个定理是我们对两个定理的灵活运用的基础,一方面从两个定理的条件和结论上区分,另一方面从两个定理的作用上加以区分.
(二)本周学习与研究中的难点
理解分清三垂线定理及其逆定理中各条直线之间的关系;灵活运用直线与平面垂直的判定定理、三垂线定理及其逆定理是本周学习与研究中的两个难点.
突破第一个难点,关键是掌握定理中所指的“三垂一”关系:(1)垂线PA与平面α的垂直关系;(2)射影AD与α上直线l的垂直关系;(3)斜线PO与α上直线l的垂直关系.
突破第二个难点关键是加强训练,特别是要消除“三垂线定理及其逆定理中的平面一定是水平放置的平面”的错觉,应能在各种“环境”中找到使用定理的条件——“一面四线”.因此其中的灵活性并非轻而易举地获得,得进行大量的训练,从训练中去体会它们的灵活性.
三、例题点评
例1、如图所示P—ABC中,AP⊥平面ABC,底面△ABC是斜边为AB的直角三角形,AE⊥PB于E,AF⊥PC于F,求证:PB⊥平面AEF.

[分析、解答、点评]
例2、在空间四边形ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.
[分析、解答、点评]
例3、在正方体ABCD—A1B1C1D1中,P为DD1的中点,O为底面ABCD的中心,求证:B1O⊥PA.
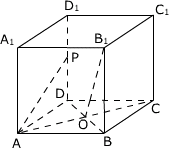
[分析、解答、点评]
例4、已知△ABC是锐角三角形,AD⊥平面ABC,H是点A在平面DBC内的射影,求证H不可能是△DBC的垂心.
[解答]
|