|
一、一周知识概述
本周学习内容是高二(下)数学第九章的第三节,即§9.3直线和平面平行与平面和平面平行.
在本周的课本学习中,我们学习两个知识点,直线和平面平行,平面和平面平行.通过这周的学习,我们理解了直线和平面平行,平面和平面平行等基本概念;学会如何判定直线和平面平行,平面和平面平行,同时学到了直线和平面,平面和平面平行的性质.
二、重、难点知识的归纳与剖析
(一)本周学习与研究中的三个重点
1、直线和平面平行的判定定理
直线和平面平行的判定定理,是通过直线和直线平行来判定直线和平面平行.这里所说的直线和直线,是指平面内的一条直线和平面外的一条直线.这个定理用符号来表示即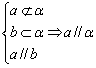 ,应用此定理时,要注意3个条件必须具备. ,应用此定理时,要注意3个条件必须具备.
2、直线和平面平行的性质定理
直线和平面平行的性质定理,是由直线和平面平行推出直线和直线平行.这里所说的直线和直线,是指与平面平行的一条直线和过这条直线的平面与已知平面(线面平行中的哪个面)的交线.这个定理用符号来表示,即 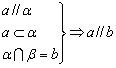 . .
这里要防止“一条直线平行于一个平面,就平行于这个平面内的一切直线”的错误理解.
在直线和平面的位置关系中,平行关系不仅应用较多,同时又是学习平面和平面位置关系的基础,因此直线和平面平行的判定定理和性质定理是§9.2节的两个重点.
3、平面和平面平行的判定定理和两个平面平行的性质
(1)两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
定理中的条件缺一不可,用符号语言表示为: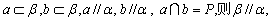 两个平面平行问题的判定或证明,是将其转化为一个平面内的直线与另一个平面平行的问题,即“线面平行,则面面平行”,必须注意这里的“线面”是指一个平面内的两条相交直线和另一个平面. 两个平面平行问题的判定或证明,是将其转化为一个平面内的直线与另一个平面平行的问题,即“线面平行,则面面平行”,必须注意这里的“线面”是指一个平面内的两条相交直线和另一个平面.
(2)两个平面平行的性质:
①两个平面平行,其中一个平面内的直线必平行于另一个平面.但这两个平面内的所有直线并不一定相互平行.它们可能是平行直线,也可能是异面直线,但不可能是相交直线.
②两个平面平行的性质定理指出两个平面平行时所具有的性质:如果两个平面平行同时与第三个平面相交,那么它们的交线平行.
③一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.
(二)本周学习与研究中的两个难点
1、线线平行、线面平行、面面平行之间的相互转化
线线平行、线面平行、面面平行之间的相互转化,是我们同学们学习中的难点.两平面关系转化为直线与平面关系,直线与直线关系是两个平面平行的性质定理的一个主要特点,我们要充分理解判定定理和性质定理之间的联系与区别,适时地进行直线与直线,直线与平面,两平面之间关系的转化.
线线关系或面面关系及线面关系的相互转化关系如下表所示:

此外,我们可总结出:证明两直线平行的方法有:
(1)依定义采用反证法;
(2)利用公理4;
(3)线面平行的性质定理;
(4)面面平行的性质定理.
证明直线和平面平行的方法有:
(1)依定义采用反证法;
(2)线面平行的判定定理;
(3)面面平行的性质.
2、反证法结合线面垂直的定义在证明中的应用
这一点同学们可通过证明教材P21例1、例3及课后练习的第3题的训练,从中悟出反证法证明问题的巧妙性.
三、例题点评
例1、已知A、B、C、D四点不共面,M、N是分别是△ABD和△BCD的重心,求证:MN∥平面ACD.
分析:
证明平面外的一条直线和该平面平行,只要在平面内找到一条直线和已知直线平行即可.即要证线面平行,必须先证明线线平行.本题可利用平面几何中的有关三角形重心的性质寻求这种线线平行关系.
解答:如图,连结BM,BN并延长分别交AD、DC于P、Q两点,连PQ.
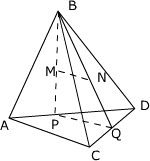
∵M、N分别是△ABD和△BCD的重心,
∴ P、Q分别是AD、DC中点.
又∵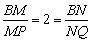 , ,
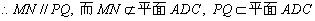 , ,
∴ MN∥平面ACD.
点评:
证明线面平行,主要找线线平行,实现线线平行,线面平行,面面平行间的相互转化.
例2、在棱长为a的正方体ABCD-A1B1C1D1中,设M,N,E,F分别是棱A1B1,A1D1,C1D1,B1C1的中点.
(1)求证:E、F、B、D四点共面
(2)求证:面AMN∥平面EFBD
分析:
(1)要证四点共面,只须判断出EF所在直线与BD所在直线互相平行即可.(2)要证明面面平行,只须证明出线面平行即可.
解答:(1)分别连结B1D1,ED,FB,则由正方体性质得B1D1//BD,
∵ E,F分别是D1C1和B1C1的中点,
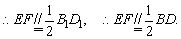
∴ E,F,B,D四点共面;
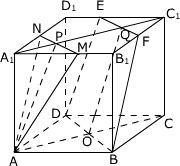
(2)连结A1C1交MN于P点,交EF于点Q,连结AC交BD于点O,分别连结PA,QO.
∵ M、N为A1B1,A1D1的中点,
∴ MN//EF, EF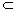 平面EFDB. 平面EFDB.
∴ MN∥面EFDB.

点评:
判定或证明两个平面平行的方法主要是利用两个平面平行的判定定理,将面面平行问题转化为线面平行,然后又将线面平行问题转化为线线平行问题,实现这之间的转化,具体如下:

例3、α、β是两个不重合的平面,可判定平面α与平面β平行的是( )
A.α、β都垂直于平面γ
B.α内不共线的三点到平面β的距离都相等
C.l、m是平面α内两条直线,且l∥β,m∥β
D.l、m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
分析:
本题是属于基本概念类的问题,其实是下列哪个选项可以推证出α∥β.对于有的选项我们只要列举反例即可,也可以用淘汰法解选择题.
解答:
考查四个选项:对于A,设直线c⊥平面γ,经过直线c作平面α和平面β,即α⊥γ且β⊥γ.但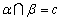 ,即α与β不平行,从而选项A不正确; ,即α与β不平行,从而选项A不正确;
对于B,条件极具有迷惑性,极易错误地判定B是对的.这是因为“α内不共线三点到β距离都相等”,易造成下列两个错觉,一是不共线三点可确定两条相交直线,二是由距离相等,极易认为相交线均平行于β.其实B中条件交没有指明三点在β的同一侧,也就是说明三点可能在β的两侧.虽然到β的距离都相等,但α与β仍是相交的.所以B也不正确;
对于C,当α、β相交于直线c,并且l、m是α内都与c平行的直线,则有l∥m,但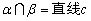 ,即α和β不平行.从而选项C也不正确; ,即α和β不平行.从而选项C也不正确;
对于D,由于平行于两条异面直线的平面必垂直于这两条异面直线的公垂直线,所以α和β都垂直于异面直线l、m的公垂线,从而α和β平行.即D是正确的.
例4:求证:过平面α内一点A,所作与α平行的直线在同一平面内.
分析:先由两相交直线确定一个平面β,然后再证过A的任一与α平行的直线在β内.
证明:如图,设过A的两直线a、b确定平面β,
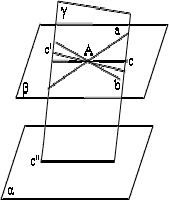
∵ a∥α,b∥α,a∩b=A,∴ α∥β.
过A任作一直线c,且c∥α,若c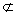 β, β,
过c作平面γ,设γ∩β=c′,γ∩α=c″.
由c∥α,知c∥c″,由α∥β,知c′∥c″.
从而在平面γ内过点A有c,c′两条相交直线与c″平行.
这是不可能的,故c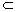 β. β.
|