一、一周知识概述

　　本周学习内容是高二下数学第九章的第七节，即直线和平面所成的角与二面角.

　　在本周的课本学习中，我们首先学习到平面的斜线和平面所成的角，二面角以及二面角的平面角这些概念，从概念中归纳出求直线和平面所成的角以及二面角的平面角的求法，即将这些空间角转化成平面内两条相交直线所成的角．在学习二面角的概念时掌握其一种特殊情况：平面的垂直关系．学会如何利用两平面垂直的判定定理判定两个平面是否垂直，又会利用两平面垂直的性质来求解相关问题，其中还了解到一个比较有用的的定理；最小角定理：cosθ=cosθ1cosθ2，最后学习了一些运用相关知识进行解题实践．

二、重、难点知识的归纳与剖析

（一）本周学习与研究中的四个重点

1、直线与平面所成的角的概念及求法

　　（1）直线与平面所成的角的定义

　　一个平面的斜线和它在这个平面内的射影的夹角叫做这条斜线和这个平面所成的角（或斜线和平面的夹角）.

　　（2）斜线在平面上的射影

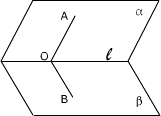
　　设O是斜线上不同于斜足A的任一点，过O作OB⊥α于B，则AB所在直线叫斜线OA在平面α上的射影，如图所示．

　　理解这一概念应注意两点：一是点O的任意性；二是斜线在平面上的射影是过斜足和垂足的一条直线而不是线段.

　　（3）直线和平面所成的角的求法

　　转化成直线和它在平面内的射影这一平面内的相交直线所成的角来处理，具体操作如下：

　　①在直线上任取一点作平面的垂线，连结垂足和斜足得到射影；

　　②在直角三角形中计算直线和平面所成角的大小.

　　此外还有向量法.

2、二面角及二面角的平面角的概念和求法

　　（1）二面角及二面角的平面角定义

　　从一条直线l出发的两个半平面α、β所组成的图形叫做二面角．该直线l称为二面角的棱，两个半平面α、β均称为二面角的面，二面角记为α—l—β.

　　一个平面垂直于二面角α—l—β的棱l，且与两个半平面的交线分别是射线OA、OB，O为垂足，则∠AOB叫做二面角α—l—β的平面角.

　　二面角的概念可类比角的概念来理解.

　　（2）二面角的平面角的作法和求解方法

　　根据定义来作二面角的平面角，方法大体有三种：

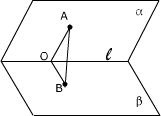
　　①过棱上的任一点O，分别在两半平面内作棱的垂线，则这两条线所成的角即为二面角的平面角，如图所示，∠AOB即为所求，此法亦称定义法.

　　②垂面法：在二面角的棱上任选一点，过该点作棱的垂面，垂面与两个半平面相交，则交线所成的角为二面角的平面角.

　　③在其中一平面α内任取一点A，过A作AB⊥β于B，过B作BO⊥l于O，连AO，则∠AOB为所求二面角的平面角，此法亦称三垂线法.

　　求二面角的平面角的方法(步骤)——转化为平面角来求.

　　①先作出二面角的平面角；

　　②解三角形求角或应用有关平面几何知识求出平面角.

3、两平面垂直的判定定理和性质定理

　　（1）判定定理：如果一个平面过另一个平面的一条垂线，那么这两个平面互相垂直.

　　（2）性质定理：如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面.

　　从两个平面垂直的判定定理和性质定理中，可以看出平面与平面的垂直问题可转化为直线与平面垂直的问题，即从线面垂直可得出面面垂直，反过来，由面面垂直又可推得线面垂直．这说明线面垂直与面面垂直之间有密切关系，可以互相转化.

（二）本周学习与研究中的两个难点

1、最小角定理即公式：cosθ=cosθ1cosθ2的灵活应用.

　　公式cosθ=cosθ1cosθ2的灵活应用的关键是熟记这三个角的含义和关系．θ表示斜线与平面内不同于射影的直线所成的角，θ1表示斜线与斜线在平面上的射影所成的角，θ2表示斜线在平面上的射影与平面内不同于射影的直线所成的角，在斜线与平面内的直线所成的角中θ1最小．

　　公式cosθ=cosθ1cosθ2的应用类型主要有下列几种：

　　（1）利用其求二面角的大小；

　　（2）利用其实现不在同一平面的角间的转化；

　　（3）利用其判断一些线线、线面关系．

　　掌握公式的灵活应用，应先在头脑中建立包含这三个角的立体模型，并熟记它们的位置，然后会推导这一公式，从推导中去摸索和掌握这三个角间的关系，最后通过适当的练习进行巩固．

2、空间角的求法

　　空间的角的求解贯穿整个立体几何的始终，一方面通过它们的求解，可以检验立体几何中相关概念的掌握情况，另一方面通过它们的求解，可以培养同学们的空间想象能力、逻辑推理能力、思维的转换能力，其间的变化之多之妙亦构成同学们学习立体几何的绊脚石，亦能激起我们学习数学的兴趣.突破这一难点，最好的方法莫过于“熟能生巧”——多练，从练习中去体会，从练习中去升华.

三、例题点评

例1、正四面体ABCD，E为棱AD的中点，连CE，求CE和平面BCD所成角的正弦值.

[解析]

例2、已和VC是△ABC所在平面的一条斜线，点N是V在平面ABC上的射影，且在△ABC的高CD上，AB=a，VC与AB之间的距离为h，点M∈VC，如图．

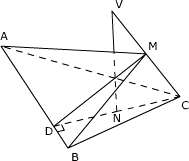
（1）证明：∠MDC是二面角M—AB—C的平面角；

（2）当∠MDC=∠CVN时，证明VC⊥平面AMB.

[解析]

例3、如图，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱PA⊥平面ABCD，E、F分别是AB、PC的中点．

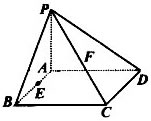
(1)求证：CD⊥PD；

(2)求证：EF∥平面PAD；

(3)当平面PCD与平面ABCD成多大角时，直线EF⊥平面PCD？

[解析]

例4、如图所示，四棱锥P—ABCD底面为一直角梯形，BA⊥AD，CD⊥AD，且AB=2，CD=4，侧面PAD⊥底面ABCD，侧面PBC为边长等于10的正三角形.

（1）求PC与底面所成角正弦值的大小；

（2）求侧面PAD与侧面PBC所成的二面角的余弦值.

[解析]