|
一、一周知识概述
本周我们学习了,带电粒子在磁场中的运动,质谱仪、回旋加速器,安培分子电流假说,磁性材料三节内容。重点是带电粒子在磁场中的运动规律:当带电粒子的初速度方向和磁场方向垂直时,粒子在匀强磁场中做匀速圆周运动,半径 ,周期 ,周期 。质谱仪、回旋加速器都是根据带电粒子在磁场中运动规律设计的。安培分子电流假说、磁性材料,是从理论上来解电与磁的关系,即磁的电本性,此外还要注意宏观带电体,在电场、磁场、重力场中运动的情况,要根据各个场对带电粒子作用的特点综合的分析带电粒子的运动。 。质谱仪、回旋加速器都是根据带电粒子在磁场中运动规律设计的。安培分子电流假说、磁性材料,是从理论上来解电与磁的关系,即磁的电本性,此外还要注意宏观带电体,在电场、磁场、重力场中运动的情况,要根据各个场对带电粒子作用的特点综合的分析带电粒子的运动。
二、重、难点知识归纳与讲解
(一)带电粒子在匀强磁场中的运动规律
1、带电粒子的速度方向若与磁场方向平行,带电粒子不受洛伦兹力作用,将以入射速度做匀速直线运动。
2、带电粒子若垂直进入匀强磁场且只受洛伦兹力的作用,带电粒子一定做匀速圆周运动,其轨道平面一定与磁场垂直。
由洛伦兹力提供向心力,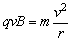 得轨道半径: 得轨道半径: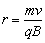 。 。
由轨道半径与周期的关系得: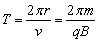 。 。
可见,周期与入射速度和运动半径无关。荷质比相同的带电粒子,当它们以不同的速度在磁场中做匀速圆周运动时,无论速度相差多大,由于其运动半径,与速度成正比,所以它们运动的周期都相同。
(二)质谱仪
利用不同质量而带同样电量的带电粒子在磁场中做匀速圆周运动的轨道半径不同,可以制成测定带电粒子质量的仪器——质谱仪。
如图所示,粒子带电量为q,质量为m,经加速电压U加速后进入匀强磁场中,在加速电场中,由动能定量得: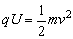 ,在匀强磁场中轨道半径: ,在匀强磁场中轨道半径: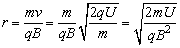 ,所以粒子质量 ,所以粒子质量 。 。
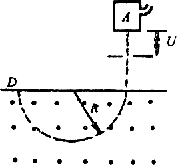
(三)回旋加速器的工作原理
粒子源位于两D形盒的缝隙中央处,从粒子源放射出的带电粒子经两D形盒间的电场加速后,垂直磁场方向进入某一D形盒内,在洛仑兹力的作用下做匀速圆周运动,若带电粒子的电荷量为q,质量为m,进入D形盒时速度为v,匀强磁场的磁感应强度为B。
使高频电源的周期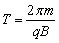 ,则当粒子从一个D形盒飞出时,缝隙间的电场方向恰好改变,带电粒子在经过缝隙时再一次被加速,以更大的速度进入另一个D形盒,以更大的速率在另一D形盒内做匀速圆周运动……;利用缝隙间的电场使带电粒子加速,利用D形盒中的磁场控制带电粒子转弯,每经过缝隙一次,带电粒子的速度增大一次,粒子的速度和动能逐次增大,在两D形盒内运动的轨道半径也逐次增大,设粒子被引出D形盒前最后半周的轨道半径的R,则带电粒子从加速器飞出的速度和动能达到最大分别为: ,则当粒子从一个D形盒飞出时,缝隙间的电场方向恰好改变,带电粒子在经过缝隙时再一次被加速,以更大的速度进入另一个D形盒,以更大的速率在另一D形盒内做匀速圆周运动……;利用缝隙间的电场使带电粒子加速,利用D形盒中的磁场控制带电粒子转弯,每经过缝隙一次,带电粒子的速度增大一次,粒子的速度和动能逐次增大,在两D形盒内运动的轨道半径也逐次增大,设粒子被引出D形盒前最后半周的轨道半径的R,则带电粒子从加速器飞出的速度和动能达到最大分别为:
 。 。
(四)安培分子电流假说
1、在原子、分子中有一种环形电流——分子电流。分子电流使每个物质微粒都成为一个小磁体,它的两侧相当于两个磁极。
2、磁铁内部的分子电流是由原子内部电子的运动形成的。可见,磁铁和电流产生磁场的本质都一样,那就是:运动电荷可以产生磁场。
(五)磁性材料
1、任何物质都是由大量的分子组成的,因而任何物质都能被外磁场或多或少地磁化。磁化的过程,就是使分子电流的取向从杂乱无章变成大致相同的过程。
2、根据物质在外磁场中表现出的特性,物质可粗分为三类:顺磁性物质、抗磁性物质和铁磁性物质。其中把顺磁性物质、抗磁性物质称为弱磁性物质,铁磁性物质称为强磁性物质。
3、磁性材料通常是指强(铁)磁性物质,磁性材料按磁化后去磁的难易可分为两类:
(1)软磁性材料:容易去磁的物质。如软铁、硅钢、镍铁合金和锰锌铁氧体、镍锌铁氧体等。适用于需要反复磁化的场合。
(2)硬磁性材料:不易去磁的物质。如碳钢、钨钢、铝镍钴合金和钡铁氧化、锶铁氧体等。适合制成永磁体。
三、重、难点知识剖析
1、带电粒子作匀速圆周运动的圆心、半径及运动时间的确定:
(1)圆心的确定,因为洛仑兹力f指向圆心,根据f⊥v,画出粒子运动轨迹中任意两点(一般是射入和射出磁场的两点)的f的方向,其延长线的交点即为圆心。
(2)半径的确定和计算,半径的计算一般是利用几何知识,常用解三角形的方法。
(3)在磁场中运动时间的确定,利用圆心角与弦切角的关系,或者是四边形内角和等于360°计算出圆心角θ的大小,由公式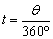 ,可求出运动时间。 ,可求出运动时间。
2、带电粒子在复合场中的运动,这里所说的复合场是磁场与电场的复合场,或者是磁场与重力场的复合场,或者是磁场和电场、重力场的复合场,当带电粒子在复合场中所受合外力为零时,所处状态是静止或匀速直线运动状态;当带电粒子所受合外力只充当向心力时,粒子做匀速圆周运动;当带电粒子所受合外力变化且与速度方向不在一条直线上时,粒子作非匀变速曲线运动。除了要写出相应的受力特点的方程之外,还要用到运动学公式,或者从能量的观点(即动能定理或能量守恒定律)写出方程,联立求解。注意微观带电粒子在复合场中运动时,一般不计重力。
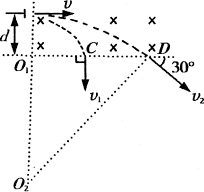
例1、如图所示,一束电子平行于匀强磁场边界入射,入射点到边界的距离为d,其中有的电子以速度v1垂直于磁场边界从磁场中射出,有的以速度v2与边界成30°角从磁场射出,则:
(1)电子圆周运动轨道半径之比R1︰R2为多少?
(2)电子运动速度比v1︰v2为多少?
解析:
(1)如图所示,过A、C两点分别作垂直于速度方向直线,相交于O1点:过A、D两点分别作垂直于速度方向直线,相交于O2,O1、O2为两个圆周的圆心。
从C点射出的电子圆周圆心在界线上,因此圆周半径R1=d.
设从D点射出的电子圆周运动轨道半径为R2。
在Rt△O1O2D中,∠O1O2D=30°,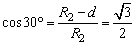 。 。
得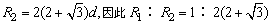 。 。
(2)根据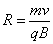 得 得 , ,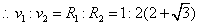 . .
例2、如图所示,虚线为有界磁场的竖直界面所在处,其区域宽度为d,磁场磁感强度 为B,方向垂直纸面向里,有一带电粒子从磁场中央O点出发,粒子速度大小为v,方向垂直磁场且与水平方向成30°角,粒子质量为m、电量为q,不计粒子重力,若要求粒子能从左边边界射出磁场,则对粒子速度v的要求如何?
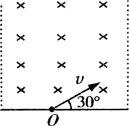
解析:
电粒子在匀强磁场中作匀速圆运动时,其轨道半径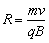 ,即R∝v,因此要确定粒子速度大小取值范围,须从分析轨道半径取值范围入手。 ,即R∝v,因此要确定粒子速度大小取值范围,须从分析轨道半径取值范围入手。
(1)若粒子作圆周运动恰好经过左边边界并与边界线相切,则其对应轨道如左图所示,设粒子对应速度大小v1,轨道半径为R1。
根据粒子经过O、A两点的速度方向确定圆弧轨迹圆心O1,则有:

而 。 。
要使粒子从左边界射出磁场,其运动轨迹的半径应大于R,
因此粒子运动速度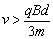 。 。
(2)若粒子作圆周运动经过右边边界恰好与边界相切,则其运动轨迹如右图所示,设其对应的速度为v2,轨道半径为R2。利用作图法确定轨迹圆心O2,则有:
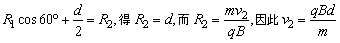 。 。
要使粒子不从右边边界射出,其运动轨道半径应小于R2,因此对速度要求: 。 。
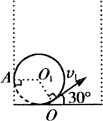
例3、如图甲所示,从左到右依次分布着水平向右的匀强磁场电场、垂直纸面向里的匀强磁场和垂直纸面向外的匀强磁场(边界是理想的)。其中匀强电场的场强为E,宽度为L,中间磁场与右侧磁场的磁感应强度均为B,质量为m、带电量为q的带电粒子从a点静止开始经电场加速,穿过中间磁场区域进入右侧磁场后,又回到a点,然后重复上述运动过程。
(1)在图上定性画出运动轨迹;
(2)求中间区域的宽度d和粒子运动的周期T。
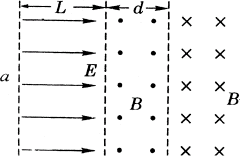
解析:
带电粒子在电场力的作用下,从a点开始做匀加速运动,在进入中间磁场后在洛伦兹力的作用下向下偏转,经一段圆弧后,进入右侧磁场后,在洛伦兹力的作用下经一圆弧后返回到中间磁场,再经一圆弧返回到电场,最后在电场中做匀减速直线运动返回到a点。该粒子的运动轨迹应具有轴对称性,故该粒子的运动轨迹如图所示。
粒子在电场中做加速运动,由动能定理可得 。 。
∴ 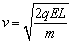 。 。
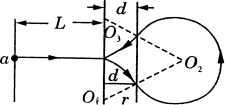
带电粒子以速度v进入磁场沿圆弧运动时,由于中间磁场与右侧磁场的磁感应强度相同,所以粒子轨迹半径相同,其大小应为 。 。
如图所示,由三段圆弧的圆心组成的三角形O1O2O3是边长为2r的正三角形,根据几何知识可得,中间磁场的宽度应为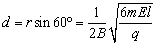 。 。
粒子运动的一个完整周期由二段直线运动和三段部分圆周运动组成。带电粒子在电场中做初速为零的匀加速直线运动,在中间磁场做圆弧运动所对应的圆角为60°,在右侧磁场中运动所对应的圆心角为300°,所以 。 。
例4、如图所示,半径为R的光滑绝缘环上套有一个质量为m、电量为+q的小球,它可沿环自由滑动。绝缘环竖直地放在相互垂直的匀强电场和匀强磁场内,电场强度为E,磁感应强度为B,方向如图所示。当球从水平直径的A端由静止释放滑到最低点时,求环对球的压力。

解析:
首先对环进行受力分析,球在运动过程中,受到重力、电场力、洛伦兹力和环的弹力四个力的作用。由这四个力的特点可知,小球在下落过程中,只有重力和电场力做功。所以当小球从A滑到C位置过程中,由动能定理可知 。 。
∴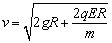
当小球滑到C位置时,小球所受的四个力均在竖直方向,由圆周运动知可得
 。 。
∴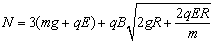 方向竖直向上。 方向竖直向上。
例5、某回旋加速器D形盒的半径R=60cm,用它加速质量m=1.67×10-27kg,电荷量q=1.6×10-19C的质子,要把静止质子加速到Ek=4.0MeV的能量,求D形盒内的磁感应强度B应多大?
解析:
D形盒的半径R可近似看作质子引出D形盒前半周的轨道半径,跟R相应的质子能量为Ek,由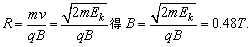
- 返回 -
|