|
一、一周知识概述
本周我们学习了光的折射、光的全反射和色散三节内容。要掌握折射定律、光介质折射率的定义及折射率与光在介质传播速度的关系,光发生全反射的条件及临界角的确定。棱镜引起的色散的规律。要能够解释自然界中的光的折射、全反射和色散现象。
二、重点知识归纳与讲解
1、折射现象和折射定理:当光线从一种介质射到另一种介质时,在分界面上,光线的传播方向发生了改变,一部分光线进入第二种介质,这种现象称为折射现象。
折射现象光路可逆。
折射光线跟入射光线和法线在同一平面内,折射光线和入射光线分别位于法线的两侧,入射角的正弦跟折射角的正弦成正比,可以用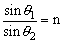 的数学公式来表达,n为比例常数。这就是光的折射定律,也叫斯涅尔定律。 的数学公式来表达,n为比例常数。这就是光的折射定律,也叫斯涅尔定律。
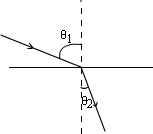
需要注意的是当光垂直入射时,即θ1=0°时,不会发生折射现象。
2、折射率:实验表明,光线在不同的介质界面发生折射时,相同入射角的情况下,折射角不同,这意味着定律中的n值是与介质有关的。当光从真空中射向不同的介质发现n值不同,表明n值只与介质的光学性质有关,人们就把n称为介质的折射率。
由折射定律得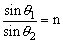 ,n越大,在θ1一定的情况下,θ2就越小,说明光改变传播方向改变的越强。研究表明,某种介质的折射率,等于光在真空中的传播速度C跟光在这种介质中的传播速度v之比,即 ,n越大,在θ1一定的情况下,θ2就越小,说明光改变传播方向改变的越强。研究表明,某种介质的折射率,等于光在真空中的传播速度C跟光在这种介质中的传播速度v之比,即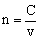 。所以,折射率大的介质光在其中传播速度小。 。所以,折射率大的介质光在其中传播速度小。
3、全反射
光从光密介质射入光疏介质。当入射角增大到某一角度,使折射角达到90°时,折射光完全消失,只剩下反射光,这种现象叫做全反射。
发生全反射的条件:(1)光从光密介质射入光疏介质;(2)入射角大于或等于临界角。
4、临界角:当光线从光密介质射向光疏介质时,入射角大于或等于某一角度C时,折射光线消失,发生了全反射现象。角度C就被称为临界角。当入射角等于临界角时,折射角等于90°,由折射定律和光路可逆可得:
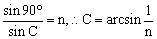

5、棱镜对光线传播方向的改变
不管是三棱镜还是多棱镜,它们对光的传播方向的改变都遵守折射定律。光通过三棱镜光路如图所示:
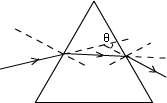
光通过棱镜后向底边偏折,偏折角θ与折射率有关,折射率大,θ大。
6、全反射棱镜
全反射棱镜是一种特殊的棱镜,横截面是等腰直角三角形,应用范围很广泛。几种典型的使用方法如图所示:
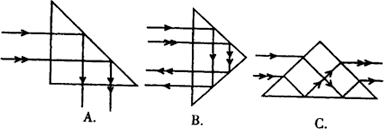
7、光的色散
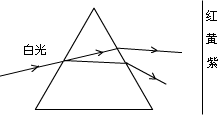
白光通过棱镜后,在光屏上会形成七色光带,如图所示,自上而下分别为红、橙、黄、绿、蓝、靛、紫。根据光线通过棱镜后的偏折角与折射率的关系,可以得到不同色的光(即频率不同)对同一种介质的折射率不同,红光的折射率最小,紫光的最大。又根据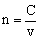 得,不同色的光在同一种介质中传播速度不同,红光速度最大,紫光速度最小。白光的色散现象说明对同一种介质,频率大的折射率大,在其中传播的速度小。 得,不同色的光在同一种介质中传播速度不同,红光速度最大,紫光速度最小。白光的色散现象说明对同一种介质,频率大的折射率大,在其中传播的速度小。
三、难点剖析
1、折射定律
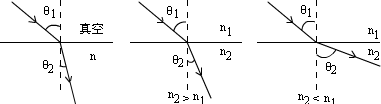
当光从真空或空气中射入折射率为n的介质时,由折射定律得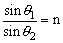 。但是当光从折射率为n1的介质中射入折射率为n2的介质时,折射定律的数学表达式就发生变化,应为 。但是当光从折射率为n1的介质中射入折射率为n2的介质时,折射定律的数学表达式就发生变化,应为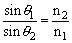 。当n2﹥n1时,光从光疏介质射入光密介质,折射角小于入射角;当n2﹤n1时,光从光密介质射入光疏介质,折射角大于入射角,光路如图。 。当n2﹥n1时,光从光疏介质射入光密介质,折射角小于入射角;当n2﹤n1时,光从光密介质射入光疏介质,折射角大于入射角,光路如图。
2、不同色的光在同一种介质中速度不同
(1)、光的颜色是由光的频率决定的。
(2)、不同颜色的光在真空中的传播速度都为C=3.0×108m/s。
(3)、不同颜色的光在同一种介质中的传播速度不同,频率越大传播速度越小。由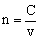 得,同一种介质对频率大的光折射率大。 得,同一种介质对频率大的光折射率大。
(4)、白光中的七种光:红、橙、黄、绿、蓝、靛、紫的频率逐渐增大。所以,同一种介质对它们的折射率逐渐增大;它们在同一种介质中的传播速度依次减小。
四、例题精讲
例1、如图所示,一储油圆筒,底面直径与桶高均为d,当筒中无油时,从某处A点恰能看到桶底边缘上的某点B。当筒内油的深度等于桶高一半时,在A沿AB方向看去,看到桶底的C点,C、B相距d/4。由此可得油的折射率n=__________;光在油中传播的速度v=_____________m/s(结果可用根式表示)。
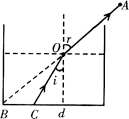
解答:
作出光路图,入射角为i,折射角为r,
根据折射定律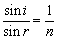 ① ①
由几何关系可得:
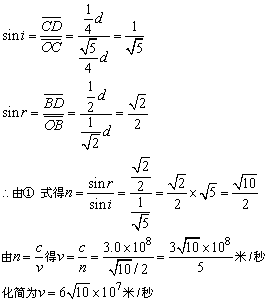
例2、如图所示,一圆柱形容器,底面直径和高度相等,当在S处沿容器边缘的A点方向观察空筒时,刚好看到筒底圆周上的B点。保持观察点位置不变,将筒中注满某种液体,可看到筒底的中心点,试求这种未知液体的折射率是多大?
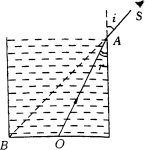
解答:
筒内未装液体时,位于S点的眼睛能看到B点以上部分,注满液体后,由O点发出的光线经液面折射后刚好进入眼睛,根据折射定律知:
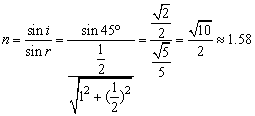
即这种未知液体的折射率n≈1.58。
例3、有人在游泳池岸边“竖直”向下观察池水的深度,看上去池水的视深为h,已知水的折射率为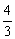 ,那么池水的实际深度H=____________。 ,那么池水的实际深度H=____________。
解答:
由池底某点p发出的光线,在水中和空气中的光路如图所示。由于观察者在岸边“竖直”向下观看,所以光线在水面处的入射角θ1和折射角θ2都很小,根据数学知识可知:

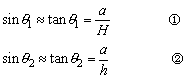
根据折射定律有:
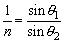
将①②两式代入③式得:
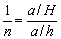
解得池水实际深度为:
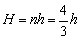 。 。
例4、(全国卷)雨过天晴,人们常看到天空中出现彩虹,它是由阳光照射到空中弥漫的水珠上时出现的现象。在说明这个现象时,需要分析光线射入水珠后的光路,一细束单色光线射入水珠,水珠可视为一个半径为R的球,球心O到入射光线的垂直距离为d,水对该光束的折射率为n。
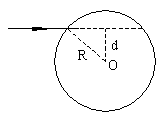
(1)在图上画出该束光线射入水珠内经一次后射后又从水珠中射出的光路图。
(2)求这束光线从射向水珠到射出水珠每一次偏转的角度。
讲解:
(1)光路如图(a)所示。
(2)以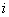 、 、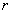 分别表示入射光线的入射角、折射角,由折射定律有 分别表示入射光线的入射角、折射角,由折射定律有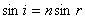 以 以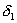 、 、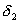 、 、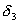 表示每一次偏转的角度,如图2-8-4(b)所示,由反射定律、折射定律和几何关系可知 表示每一次偏转的角度,如图2-8-4(b)所示,由反射定律、折射定律和几何关系可知
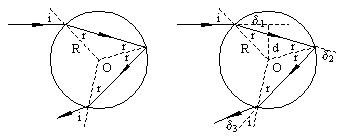
(a) (b)
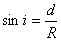 , ,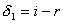 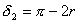 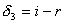
由以上各式解得: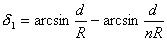 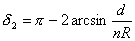
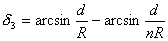 。 。
答案:
(1)如图2-8-4(a)所示
(2) , , 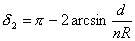 , , 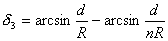
例5、如图所示,有一玻璃直角三棱镜ABC,其临界角小于45°,一束平行于BC的白光射到AB面,在光束射出三棱镜时(设光线在棱镜内先射至BC边上)()。
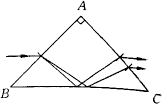
A.从BC面出射的是白色光束
B.从AC面出射的是白色光束
C.从AC面出射的是有色的不平行光束
D.从AC面出射的是平行于入射线的有色光束
解答:
一束平行于BC边的白光射到AB面上,入射角i=45°,经AB面折射后,各种色光的折射角略有不同,红光的折射率最小,紫光的折射率最大,则红光的折射角最大,但各种色光的折射角都小于45°,射向BC面上时,入射角都将大于45°,(其中红光的入射角最大),因此各种色光都不会从BC面射出,即发生全反射。反射光线射至AC面上时,由于对称性可知,入射角等于AB上的折射角,所以由AC面射出的光线将与AB面上的入射线平行。但各种色光已有所偏移,最下面是红光,最上面是紫光。故D正确。
- 返回 -
|