1、等比数列的定义
如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q表示．
注意：
（1）q是指从第2项起每一项与前一项的比，顺序不要错，即
（2）由定义可知，等比数列的任意一项都不为0，因而公比q也不为0.
（3）公比q可为正数、负数，特别当q=1时，为常数列a1,a1,……；q=－1时，数列为a1,－a1,a1,－a1,…….
（4）要证明一个数列是等比数列,必须对任意n∈N＋,an＋1÷an=q,或an÷an－1=q（n≥2）都成立.
2、等比数列的通项公式
由a2=a1q，a3=a2q=a1q2，a4=a3q=a1q3，……，归纳得出an=a1qn－1.此公式对n=1也成立.
注意：
（1）通项公式an=a1qn－1是通过不完全归纳法得出的.
（2）由等比数列通项公式可得
，当q>0且q≠1时，y=qx是一个指数函数，而
是一个不为0的常数与指数函数的积.因此等比数列{an}的图象是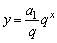
的图象上的一群孤立点.
（3）公式中含四个量a1,an,d,n，如已知任意三个，可求第四个量.
3、等比中项
如果在a与b中间插入一个数G，使a，G，b成等比数列，那么G叫做a与b的等比中项．
注意：
（1）如果G是a与b的等比中项，那么
，即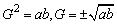
.所以两个同号的数才有等比中项，而且等比中项有两个，它们互为相反数.
（2）当a>0,b>0时，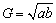
也叫做a，b的几何平均数.
（3）在等比数列中，从第二项起，每一项（有穷数列末项除外）都是它前后两项的等比中项.
4、等比数列的判定方法
（1）an=an－1·q（n≥2），q是不为零的常数，an－1≠0
{an}是等比数列.
（2）an2=an－1·an＋1（n≥2, an－1,an,an＋1≠0）
{an}是等比数列.
（3）an=c·qn（c，q均是不为零的常数）
{an}是等比数列.
5、等比数列的性质
设{an}为等比数列，首项为a1，公比为q.
（1）当q>1，a1>0或0<q<1，a1<0时，{an}是递增数列；当q>1，a1<0或0<q<1,a1>0时，{an}是递减数列；当q=1时，{an}是常数列；当q<0时，{an}是摆动数列.
（2）an=am·qn－m（m、n∈N*）.
（3）当m＋n=p＋q（m、n、q、p∈N*）时，有am·an=ap·aq.
（4）{an}是有穷数列，则与首末两项等距离的两项积相等，且等于首末两项之积.
（5）数列{λan}（λ为不等于零的常数）仍是公比为q的等比数列；若{bn}是公比为q′的等比数列，则数列{an·bn}是公比为qq′的等比数列；数列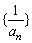
是公比为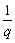
的等比数列；{|an|}是公比为|q|的等比数列.
（6）在{an}中，每隔k(k∈N*)项取出一项，按原来顺序排列，所得新数列仍为等比数列且公比为qk＋1.
（7）当数列{an}是各项均为正数的等比数列时，数列{lgan}是公差为lgq的等差数列.
（8）{an}中，连续取相邻两项的和（或差）构成公比为q的等比数列.
（9）若m、n、p（m、n、p∈N*）成等差数列时，am、an、ap成等比数列.
6、等比数列的前n项和公式
设等比数列a1,a2,a3,…,an，…，它的前n项和是Sn=a1＋a2＋…＋an，根据等比数列的通项公式可将Sn写成Sn=a1＋a1q＋a1q2＋…＋a1qn－1. …①
①两边乘以q得qSn=a1q＋a1q2＋a1q3＋…＋a1qn …②
两式相减得 （1－q）Sn=a1－a1qn，
由此得q≠1时等比数列{an}的前n项和的公式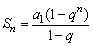
.
因为an=a1qn－1，所以上面公式还可以写成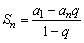 
.
当q=1时，Sn=na1.
注意：
①公比为1与公比不为1时公式不同；
②当已知a1,q,n时，用公式 
；当已知a1,q,an时，用公式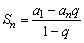 
.
③问Sn公式推导可以有几种方法？
证法二：由等比定义知：
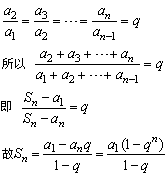
证法三：
在解决等比数列问题时，如已知a1,an,q,n,Sn中任意三个，就可求出其余2个.
7、等比数列前n项和的一般形式
一般地，如果a1,q是确定的，那么
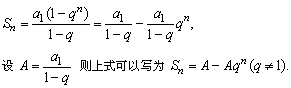
8、等比数列的前n项和的性质
（1）若某数列前n项和公式为Sn=an－1(a≠0,±1)，则{an}成等比数列.
（2）若数列{an}是公比为q的等比数列，则
（ⅰ）Sn＋m=Sn＋qn·Sm.
（ⅱ）在等比数列中，若项数为2n(n∈N*)，则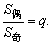
（ⅲ）Sn,S2n－Sn,S3n－S2n成等比数列.
，求通项公式.
，已知
，求等差数列的通项a
的等比中项为
的等差中项为1，求等差数列{a
