|
一、一周知识概述
本周主要是讲解等差数列前n项和公式、性质及应用,通过学习,使同学们了解等差数列前n项和公式推导过程(倒序求和),掌握等差数列前n项和公式的两种不同形式,并能利用它们解决一些实际问题,培养学生对数学的理解能力,观察能力以及对数学公式的应用能力和分析问题、解决问题的能力.
二、重难点知识概述
1、在推导等差数列前n项和公式的过程中用到了数列求和的两种基本思想方法——分组求和法及倒序相加法.
2、前n项求和公式为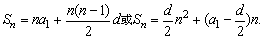
当d≠0时,Sn是关于n的二次函数且常数项为0,可以运用二次函数的观点和方法来认识求等差数列的前n项和问题,如可以根据二次函数的图象了解Sn的增、减变化及最值等问题.当d=0时,{an}是常数列,Sn=na1,若a1不为零,则Sn是关于n的一次(正比例)函数,若a1=0,则Sn=0.
3、设数列{an}是等差数列,项数为m,其奇数项之和为S奇,偶数项之和记为S偶,那么当项数m为偶数2n时,S偶-S奇=nd,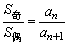 ;当项数m为奇数2n+1时,S奇-S偶=an+1, ;当项数m为奇数2n+1时,S奇-S偶=an+1,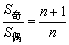 .(不必强记这些结论,关键是掌握其证法,对于提高解题的灵活性是有益的.) .(不必强记这些结论,关键是掌握其证法,对于提高解题的灵活性是有益的.)
4、若{an},{bn}为等差数列,前n项和为An,Bn,则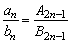 . .
5、若{an}为等差数列,则Sk,S2k-Sk,S3k-S2k,…,仍为等差数列.
6、等差数列前n项和Sn是关于n的二次函数(d≠0),而且常数项为零,这是等差数列前n项和公式的形式特征,我们可以根据这个特征,判断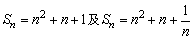 不可能是等差数列的前n项和,利用Sn=an2+bn有时可使计算更简便. 不可能是等差数列的前n项和,利用Sn=an2+bn有时可使计算更简便.
7、在解决等差数列有关问题时,涉及的五个量an,n,d,a1,Sn通过方程组知三可求二.
8、前n项和Sn与通项an的关系是:Sn=a1+a2+…+an
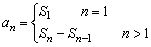
由Sn求an一定要讨论n=1,然后进行综合.
二、例题讲解
例1、在等差数列{an}中,已知a6+a9+a12+a15=34,求前20项之和.
[解答]
例2、已知数列{an}的前n项和为Sn,(1)设Sn=3n2-2n,求证{an}成等差数列;(2)若Sn=3n2-2n-1,问{an}是否为等差数列?
[解答]
例3、等差数列{an}中,a1>0,前n项之和为Sn,且S7=S13,问n为何值时,Sn最大?
[解答]
例4、设等差数列的前n项和为Sn.已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出S1,S2,…,S12中哪一个值最大,并说明理由.
[解答]
例5、在等差数列{an}中,a1=-60,a17=-12,求数列{|an|}的前n项和.
[解答]
例6、等差数列{an}的前m项和为30,前2m项和为100,则它的前3m项和为__________.
[解答]
例7、含2n+1个项的等差数列其奇数项的和与偶数项的和之比为( ).
A.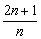 B. B. C. C.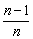 D. D.
[解答]
例8、已知两个等差数列{an},{bn},它们前n项和的比为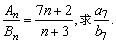
[解答]
|