|
一、基础知识总结
基础知识框图表解

二、重点知识归纳、总结
1、集合部分
解决集合问题时,首先要明确集合元素的意义,弄清集合由哪些元素组成,需要对集合的文字语言、符号语言、图形语言进行相互转化.其次,由于集合知识概念多、符号多,所以要注意集合的特性,空集的特殊性,符号的表示的特殊性.三是注意知识间的内在联系,注意集合思想与函数思想的联系,集合与不等式、解析几何、三角函数等知识的联系.
(1)集合中元素的三大特征
(2)集合的分类
(3)集合的三种表示方法
(4)集合的运算
①n元集合共有2n个子集,其中有2n-1个真子集,2n-1个非空子集;
②A∩B={x|x∈A且x∈B}
③A∪B={x|x∈A或x∈B}
④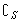 A={x|x∈S且x A={x|x∈S且x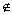 A},其中A A},其中A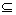 S. S.
2、不等式的解法
(1)含有绝对值的不等式的解法
①|x|<a(a>0) -a<x<a; -a<x<a;
|x|>a(a>0)  x>a,或x<-a. x>a,或x<-a.
②|f(x)|<g(x)  -g(x)<f(x)<g(x); -g(x)<f(x)<g(x);
|f(x)|>g(x)  f(x)>g(x)或f(x)<-g(x). f(x)>g(x)或f(x)<-g(x).
③|f(x)|<|g(x)|  [f(x)]2<[g(x)]2 [f(x)]2<[g(x)]2 [f(x)+g(x)]·[f(x)-g(x)]<0. [f(x)+g(x)]·[f(x)-g(x)]<0.
④对于含有两个或两个以上的绝对值符号的绝对值不等式,利用“零点分段讨论法”去绝对值. 如解不等式:|x+3|-|2x-1|<3x+2.
(2)一元二次不等式的解法
任何一个一元二次不等式,经过不等式的同解变形,都能化为ax2+bx+c>0(a>0),或ax2+bx+c<0(a>0)的形式,再根据“大于取两边,小于夹中间”得解集(若判别式△≤0,则利用配方法求解较方便).
详细解集见下表:
判别式
△=b2-4ac
|
△>0 |
△=0 |
△<0 |
二次函数
y=ax2+bx+c
(a>0)的图象
|
y=ax2+bx+c
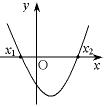
|
y=ax2+bx+c
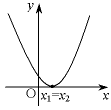 |
y=ax2+bx+c
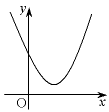 |
一元二次方程
ax2+bx+c=0
(a>0)的根
|
有两相异实根
x1,x2(x1<x2)
|
有两相等实根
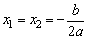
|
没有实根 |
ax2+bx+c>0
(a>0)的解集
|
{x|x<x1,
或x>x2}
|
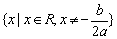
|
R |
ax2+bx+c<0
(a>0)的解集
|
{x|x1<x<x2} |
|
|
(3)分式不等式的解法
①分类讨论去分母法:

②转整式不等式法:
运用时,必须使不等式一边为0,转化为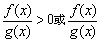 ≤0形式,则: ≤0形式,则:

(4)高次不等式的解法
3、简易逻辑知识
逻辑联结词 “或”、“且”、“非”是判断简单合题与复合命题的依据;真值表是由简单命题和真假判断复合命题真假的依据,理解好四种命题的关系,对判断命题的真假有很大帮助;掌握好反证法证明问题的步骤.
(1)命题
①简单命题:不含逻辑联结词的命题
②复合命题:由简单命题与逻辑联结词构成的命题
(2)复合命题的真值表
非p形式复合命题的真假可以用下表表示.
p且q形式复合命题的真假可以用下表表示.
p |
q |
p且q |
真 |
真 |
真 |
真 |
假 |
假 |
假 |
真 |
假 |
假 |
假 |
假 |
p或q形式复合命题的真假可以用下表表示.
p |
q |
p或q |
真 |
真 |
真 |
真 |
假 |
真 |
假 |
真 |
真 |
假 |
假 |
假 |
(3)四种命题及其相互之间的关系
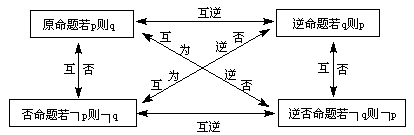
一个命题与它的逆否命题是等价的.
(4)充分、必要条件的判定
①若p q且q q且q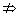 p,则p是q的充分不必要条件; p,则p是q的充分不必要条件;
②若p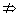 q且q q且q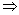 p,则p是q的必要不充分条件; p,则p是q的必要不充分条件;
③若p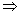 q且q q且q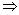 p,则p是q的充要条件; p,则p是q的充要条件;
④若p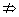 q且q q且q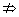 p,则p是q的既不充分也不必要条件. p,则p是q的既不充分也不必要条件.
(5)反证法
反证法是“命题与其逆否命题等价”这一理论的具体体现,用反证法证明命题的一般步骤是:
①假设命题的结论不成立.
②经过推理论证,得出矛盾.
③由矛盾判定假设不正确,从而肯定命题的结论正确.
4、运用知识、运用方法过程中应注意的主要问题
(1)正确理解集合的概念必须掌握构成集合的两个必要条件:研究对象是具体的,其属性是确定的.
(2)在判断给定对象能否构成集合时,特别要注意它的“确定性”,在表示一个集合时,要特别注意它的“互异性”、“无序性”.
(3)在集合运算中必须注意组成集合的元素应具备的性质.
(4)对由条件给出的集合要明白它所表示的意义,即元素指什么,是什么范围.用集合表示不等式(组)的解集时,要注意分辨是交集还是并集,结合数轴或文氏图的直观性帮助思维判断.空集是任何集合的子集,但因为不好用文氏图形表示,容易被忽视,如在关系式 中,易漏掉 中,易漏掉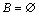 的情况. 的情况.
(5)若集合中的元素是用坐标形式表示的,要注意满足条件的点构成的图形是什么,用数形结合法解之.
(6)若集合中含有参数,须对参数进行分类讨论,讨论时既不重复又不遗漏.
(7)解不等式的基本思想是化归、转化,解含有参数的不等式常需要分类讨论,同解变形是解不等式的理论依据.
(8)学习四种命题,关键是理解命题结构及逻辑联结词“或”、“且”、“非”的含义,掌握四种命题间的关系是学习充要条件的基础.
(9)基本的逻辑知识是认识问题和研究问题不可缺少的工具,是我们进行学习、掌握和使用语言的基础,数学又是逻辑性很强的学科,因此,学习一些逻辑知识是非常必要的,通过学习和训练可以规范和提高推理的技能,发展思维能力.重点是正确使用逻辑联结词“或”、“且”、“非”,是否使用得当的依据是真值表,利用真值表再结合四种命题的充要条件可判定复合命题的真假性.注意区别一些易错的逻辑关系,如“都是”、“都不是”、“不都是”.
5、在学习和运用集合知识的过程中,须注意的几个问题
目前在中学数学教学中,集合知识主要有两方面的应用.
(1)把集合作为一种数学语言,以表达一定范围或具有某些特性的元素.例如,方程(或方程组)的解集,不等式(或不等式组)的解集,具有某种性质或满足某些条件的数集、点集、向量集(以后会学)等,因集合元素的任意性,使得集合语言有着广泛的应用性.
(2)使用集合间的运算法则或运算思想,解决某些逻辑关系较复杂的问题.例如,运用集合法判断真假复合命题和充要条件,运用集合的交集思想、并集思想、补集思想解题等.
三、学法指导
(一)要注意理解、正确运用集合概念
例1、若P={y|y=x2,x∈R},Q={y|y=x2+1,x∈R},则P∩Q等于( )
A.P B.Q C.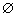 D.不知道 D.不知道
[解答]
例2、若P={y|y=x2,x∈R},Q={(x,y)|y=x2,x∈R},则必有( )
A.P∩Q=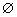 B.P B.P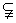 Q Q
C.P=Q D.P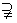 Q Q
[解答]
(二)要充分注意集合元素的互异性
集合元素的互异性,是集合的重要属性,教学实践告诉我们,集合中元素的互异性常常被学生在解题中忽略,从而导致解题的失败,下面再结合例题进一步讲解以期强化对集合元素互异性的认识.
例3、若A={2,4,a3-2a2-a+7},B={1,a+1,a2-2a+2,-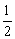 (a2-3a-8),a3+a2+3a+7},且A∩B={2,5},试求实数a的值. (a2-3a-8),a3+a2+3a+7},且A∩B={2,5},试求实数a的值.
[解答]
例4、已知集合A={x|x2-3x+2=0},B={x|x2-ax+a-1=0},且A∪B=A,则a的值为________.
[解答与点评]
(三)要注意掌握好证明、判断两集合关系的方法
集合与集合之间的关系问题,是我们解答数学问题过程中经常遇到,并且必须解决的问题,因此应予以重视.
反映集合与集合关系的一系列概念,都是用元素与集合的关系来定义的.因此,在证明(判断)两集合的关系时,应回到元素与集合的关系中去.
例5、设集合A={a|a=n2+1,n∈N*},集合B={b|b=k2-4k+5,k∈N*},试证:A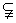 B. B.
[证明与点评]
(四)要注意空集的特殊性和特殊作用
空集是一个特殊的重要集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集.显然,空集与任何集合的交集为空集,与任何集合的并集仍等于这个集合.当题设中隐含有空集参与的集合关系时,其特殊性很容易被忽视的,从而引发解题失误.
例6、已知集合A={x|x2+(m+2)x+1=0,x∈R},若A∩R+= ,则实数m的取值范围是_________. ,则实数m的取值范围是_________.
[解答与点评]
例7、已知集合A={x|x2-3x-10≤0},集合B={x|p+1≤x≤2p-1}.若B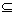 A,求实数p的取值范围. A,求实数p的取值范围.
[解答与点评]
(五)要注意集合语言与其它数学语言互译的准确性
事实上,各种数学语言形态间的互译,可为我们在更广阔的思维领域里寻找问题的解决途径,因而这种互译是我们在解题过程中常常必须做的事情.
对于用集合语言叙述的问题,求解时往往需要转译成一般的代数语言或几何语言.
例8、已知集合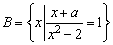 有唯一元素,用列举法表示a的值构成的集合A. 有唯一元素,用列举法表示a的值构成的集合A.
[解答与点评]
(六)要注意数形结合解集合问题
集合问题大都比较抽象,解题时要尽可能借助文氏图、数轴或直角坐标系等工具将抽象问题直观化、形象化、明朗化,然后利用数形结合的思想方法使问题灵活直观地获解.
例9、设A={x|-2<x<-1,或x>1},B={x|x2+ax+b≤0},已知A∪B={x|x>-2},A∩B={x|1<x≤3},试求a、b的值.
[解答与点评]
例10、若关于x的不等式|x+2|-|1-x|<a有解,求实数a的取值范围.
[解答与点评]
(七)要注意交集思想、并集思想、补集思想的运用
对于一些比较复杂、比较抽象,条件和结论之间关系不明朗,难于从正面入手的数学问题,在解题时,可调整思路,从问题的反面入手,探求已知与未知的关系,这样能起到反难为易,化隐为显,从而将问题得以解决,这就是“正难则反”的解题策略,是补集思想的具体应用.
有的问题,根据问题具体情况,也可采用交集思想、并集思想去处理.
例11、已知集合A={x|x2-4mx+2m+6=0,x∈R},若A∩R-≠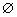 ,求实数m的取值范围. ,求实数m的取值范围.
[解答与点评]
例12、命题甲:方程x2+mx+1=0有两个相异负根;命题乙:方程4x2+4(m-2)x+1=0无实根,这两个命题有且只有一个成立,求m的取值范围.
[解答与点评]
|