例1、判断下列命题是否正确.若不正确,请简述理由.
1、直角坐标系中非负x轴是向量;
2、向量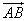 与
与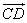 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
3、四边形ABCD是平行四边形的充要条件是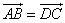 ;
;
4、若非零向量a与b的方向相同或相反,则a+b的方向必与a、b之一的方向相同;
5、三角形ABC中,必有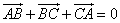 ;
;
6、若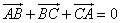 ,则A、B、C三点是一个三角形的三顶点;
,则A、B、C三点是一个三角形的三顶点;
7、|a+b|≥|a-b|.
解析:
1、不正确.∵非负x轴只有方向,没有大小.∴不是向量.
2、不正确.∴共线向量即平行向量,只要求方向相同或相反即可.
并不要求两向量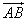 ,
,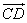 在同一直线上.
在同一直线上.
3、正确.∵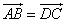 则AB与DC平行且相等.∴ABCD是平行四边形.
则AB与DC平行且相等.∴ABCD是平行四边形.
4、不正确.∴a+b可以为零向量,此时a+b方向不确定,说与a、b之一的方向相同不妥.
5、正确.∴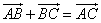 .∴
.∴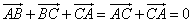 .
.
6、不正确.∴当A、B、C三点共线时,也满足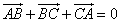 .
.
7、不正确.∴当a、b不共线时,a+b与a-b分别为以a、b为邻边的平行四边形两对角线,其长度大小不定.当a、b共线异向时反而有|a+b|<|a-b|.
∴|a+b|≥|a-b|不正确.
例2、如图,在以正方体ABCD-A1B1C1D1的顶点为起点、终点的向量中,
(1)写出所有与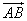 相等的向量;
相等的向量;
(2)写出所有与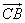 相反的向量;
相反的向量;
(3)写出与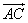 相等及相反的向量;
相等及相反的向量;
(4)写出与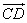 共线的向量.
共线的向量.
解析:
(1)与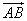 相等的向量有:
相等的向量有: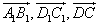 .
.
(2)与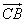 相反的向量有:
相反的向量有: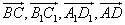 .
.
(3)与 相等及相反的向量有:
相等及相反的向量有: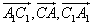 .
.
(4)与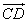 共线的向量有:
共线的向量有: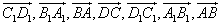 .
.
例3、已知|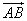 |=6,|
|=6,|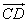 |=9,求
|=9,求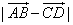 取值范围.
取值范围.
解析:
由向量加、减法的三角形法则知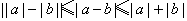 ,
,
∴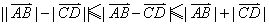 .
.
故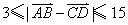 .
.
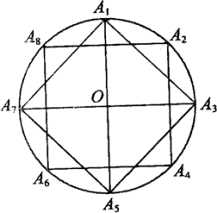
例4、如图,A1、A2、…A8是 O上的八个等分点,则在以A1、A2、…A8及圆心O九个点中任意两点为起点与终点的向量中,模等于半径的向量有多少个?模等于半径
O上的八个等分点,则在以A1、A2、…A8及圆心O九个点中任意两点为起点与终点的向量中,模等于半径的向量有多少个?模等于半径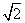 倍的向量有多少个?
倍的向量有多少个?
分析:
(1)由于A1、A2、…A8是 O上的八个等分点,所以八边形A1A2…A8是正八边形,正八边形的边及对角线长均与
O上的八个等分点,所以八边形A1A2…A8是正八边形,正八边形的边及对角线长均与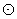 O的半径不相等.所以模等于半径的向量只可能是
O的半径不相等.所以模等于半径的向量只可能是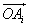 与
与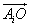 (i=1、2、…8)两类.
(i=1、2、…8)两类.
(2)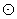 O内接正方形的边长是半径的
O内接正方形的边长是半径的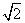 倍,所以我们应考虑与圆心O形成90°圆心角的两点为端点的向量个数.
倍,所以我们应考虑与圆心O形成90°圆心角的两点为端点的向量个数.
解:
(1)模等于半径的向量只有两类,一类是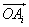 (i=1、2、…8)共8个;另一类是
(i=1、2、…8)共8个;另一类是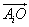 (i=1、2、…8)也有8个.两类合计16个.
(i=1、2、…8)也有8个.两类合计16个.
(2)以A1、A2、…A8为项点的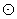 O内接正方形有两个,一个是正方形A1A3A5A7,另一个是正方形A2A4A6A8.在题中所述的向量中,只有这两个正方形的边(每一边对应两个向量)的长度为半径的
O内接正方形有两个,一个是正方形A1A3A5A7,另一个是正方形A2A4A6A8.在题中所述的向量中,只有这两个正方形的边(每一边对应两个向量)的长度为半径的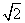 倍.∴模为半径
倍.∴模为半径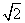 倍的向量共有4×2×2=16个.
倍的向量共有4×2×2=16个.
例5、(1)O是△ABC内的一点,若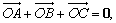 求证:O是△ABC的重心,反之是否正确?
求证:O是△ABC的重心,反之是否正确?
(2)O为△ABC的外心,H为重心,求证: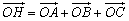 .并由此推断,已知O是△ABC的外心(或内心,或垂心),如果满足
.并由此推断,已知O是△ABC的外心(或内心,或垂心),如果满足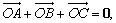 那么该三角形是什么形状?
那么该三角形是什么形状?
分析:
(1)三角形的重心分中线两段的比为2︰1;
(2)正三角形的内心、外心、垂心和重心重合.
解析:
(1)如图a所示,以OB,OC为邻边作□BOCD,则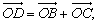
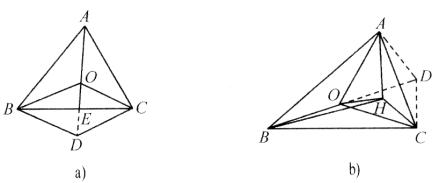
由于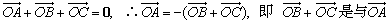 方向相反且长度相等的向量,
方向相反且长度相等的向量,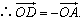
在平行四边形BOCD中,设BC与OD的交点为E,
则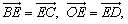 ∴AE是△ACD的BC边上的中线,且
∴AE是△ACD的BC边上的中线,且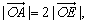 ∴点O是△ABC的重心.反之显然正确;
∴点O是△ABC的重心.反之显然正确;
(2)如图b所示,作直径BD,连DA,DC,有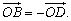
∵DA⊥AB,DC⊥BC,AH⊥BC,CH⊥AB,
∴CH∥DA,AH∥DC.从而四边形AHCD是平行四边形,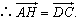
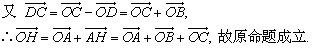
若O是ABC的外心,设△ABC的重心为H,
由已证结论知
即△ABC的外心与重心重合,故△ABC为正三角形.