|
一、一周知识概述
本周在复习初中整数指数幂、平方根、立方根的基础上学习了根式、根式的性质,分数指数幂及运算性质,并在此基础上学习了一种特殊的函数——指数函数,及其图象和性质.指数函数是这一单元的重点内容.
二、重点知识讲解
1、分数指数幂的概念及分数指数的运算性质.
(1)数a的n次方根
当n为奇数时,实数a的n次方根为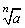 ; ;
当n为偶数时,非负数a的n次方根为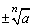 . .
(2)根式及性质
式子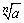 叫做根式. 叫做根式.
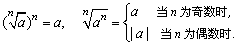
(3)分数指数幂
设a>0,且a≠1,m,n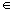 N*且n≠1, N*且n≠1,
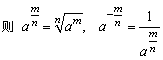 . .
(4)有理指数幂的性质
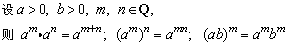
例1、化简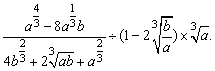
[解析]
2、指数函数的图象和性质
形如y=ax(a>0,且a≠1)的函数叫指数函数,其中x∈R.
指数函数的图象及性质.
| |
a>1 |
0<a<1 |
图
像 |
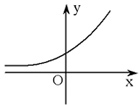 |
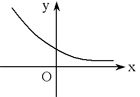 |
性
质 |
1 |
定义域:R |
2 |
值域:(0,+∞) |
x>0,y>1;x<0,0<y<1 |
x>0,0<y<1;x<0,y>1 |
3 |
过点(0,1) |
4 |
在R上是增函数 |
在R上是减函数. |
例2、若函数y=ax+m-1的图象在一、三、四象限,则( )
A.a>1 B.a>1且m<0
C.0<a<1且m>0 D.0<a<1
[解析]
例3、若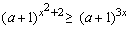 (a>-1且a≠0),求x的取值范围. (a>-1且a≠0),求x的取值范围.
[解析] 三、难点知识剖析
如何解答与指数函数有关的复合函数问题是本单元的难点.
例4、设0≤x≤2,求函数 的最大值和最小值. 的最大值和最小值.
[解析]
例5、函数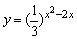 的值域是_________,单调区间是_________. 的值域是_________,单调区间是_________.
[解析]
|