一、一周知识概述

　　本周主要学习有关力的平衡及平衡条件，共点力平衡条件的应用，从单个物体的平衡延伸到连接体中某物体的平衡，介绍整体法与隔离法综合解题方法。

二、重难点知识讲解

（一）平衡状态

　物体处于静止状态或匀速直线运动状态均称平衡状态。

（二）共点力作用下物体的平衡条件

　合力为零，即：F合=0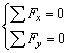

（三）利用共点力平衡条件解题步骤

1、隔离研究对象；

2、分析被隔离的对象受力情况，并画好受力图；

3、利用平行四边形定则或矢量三角形定则或正交分解法、结合平衡条件列方程求解.

正确分析受力情况是解题的关键。

（四）例题

例1、应用正交解法

　　如图所示，轻绳AO、BO受到的拉力分别为TA和TB，当改变AO的长度使θ角增大，并保持BO的水平状态，则（　）

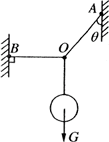
A．TA、TB都增大，且TA>TB

B．TA、TB都增大，且TA<TB

C．TA增大，TB减小

D．TA减小，TB增大

解析：先分析O点受力，以O点为坐标原点建立直角坐标系，应用平衡条件：

　　　

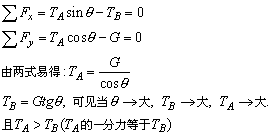
　　　故选项为A项。

答案：A

例2、分力法与平衡法

　　光滑半球形物体固定在水平地面上，球心正上方有一光滑的小滑轮，轻绳的一端系一小球，靠放在半球上的A点。另一端绕过定滑轮后用力拉住，使小球静止，如图所示，现缓慢地拉绳，在使小球沿球面由A到B的过程中，半球对小球的支持力N和绳对小球的拉力T的大小变化情况是（　）

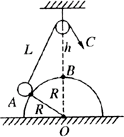
A．N变大、T变小

B．N变小，T变大

C．N变小，T先变小后变大

D．N不变，T变小

解析：

　　分析小球受力情况，应用平行四边形定则，可见拉力T与支持力N的合力等于小球的重力。由于角度未知，且为变值，应用相似三角形求解.

　　

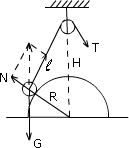
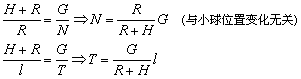
　　可见随小球上升，l→小，T→小，正确选项为D。此种解法为平衡法。

　　应用分力法，将小球受的几个力当中某一已知力进行分解，应用平行四边形定则或三角形定则求解。

答案：D

例3、整体法与隔离法

　　一均质木板边长为a，按图示对称分割，平铺在水平地面上，现用恒力F水平推A，使三部分一起向右匀速滑动而不分开，求AC间静摩擦力大小。

解析：隔离C，分析其受力情况（俯视）。

　　　

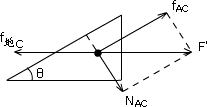
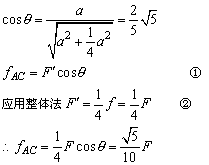
　　注意：①由于C相对A有左滑的趋势，故静摩擦力fAC的方向沿斜边向右，②选择隔离体时应使被隔离对象受力情况简单又要包含要求的力，若选择A为研究对象较麻烦。

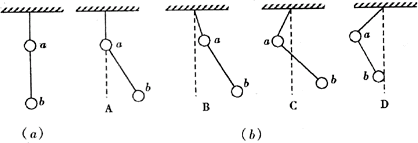
例4、用轻质细绳把两个质量未知的小球悬挂起来，如图（a）所示，今对小球a持续施加一个向左偏下30°的恒力，并对小球b持续施加一个向右偏上30°同样大的恒力，最后达到平衡，表示平衡状态的图可能是如图（b）所示中的（　）

解析：

　　本题考查应用物体的平衡条件处理连接平衡问题，可用整体法或隔离法进行分析。

　　解法一：将a、b两球及两球间的绳看做一个物体系统，以这个系统为研究对象。因为作用在a、b上恒力等大反向，其合外力平衡，而a、b受的重力竖直向下，要保持平衡，故a到悬点的细绳的力必然沿竖直方向向上，故选项A是正确的。

　　解法二：也可以分别将a、b隔离进行受力分析，分别对a、b两球列出水平分力的平衡方程即可，以c图为例，受力分析如图所示。

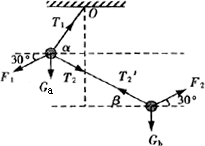
对a：水平方向有F1cos30°=T1cosα＋T2cosβ

对b：水平方向有F2cos30°=T2 cosβ

∵ F1=F2，∴ F1cosα=0

由于T1≠0，故α=90°,

∴ 正确选项是A.

- 返回 -