|
一、本周内容概述
在上学期学习了有关圆周运动的知识的基础上,新学期的第一周我们学习万有引力定律这一章。本章主要讲述万有引力定律的发现及其在天体运动中的应用,其中万有引力定律的发现、发展过程和该定律的具体运用是本章的重点。
本章按以下线索展开:开普勒对行星运动规律的描述为万有引力定律的发现奠定了基础→牛顿在前人研究的基础上发现了万有引力定律→卡文迪许用实验较准确地测定了引力常量,使得万有引力定律有了更实际的应用→利用万有引力及其有关知识讨论天体和人造卫星的运动情况。
二、重难点知识归纳与讲解
(一)万有引力定律
(1)内容:自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
(2)公式: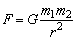
式中质量的单位用kg,距离的单位用m,力的单位用N。G为引力常量,标准值为G=6.67259×10-11N·m2/kg2.
通常取G=6.67×10-11N·m2/kg2.
(3)适用条件:只适用于质点间的相互作用,但当两个物体间的距离远大于物体本身的大小时,物体可视为质点,公式也近似成立。
质量分布均匀的球体也可用此公式计算两者间的引力大小,其中r指球心间的距离。
注意:
①两个物体间的相互吸引力是一对作用力和反作用力,总是大小相等、方向相反,遵守牛顿第三定律。
②在地球表面的物体所受的重力近似地认为等于地球对物体的引力,可知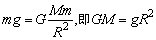 ,这是一个常用的变换,式中g是地球表面的重力加速度。 ,这是一个常用的变换,式中g是地球表面的重力加速度。
③离地面越高,物体的重力加速度越小,它和高度的关系为: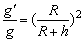 ,式中R是地球的半径,h是物体离地面的高度。 ,式中R是地球的半径,h是物体离地面的高度。
例1、两大小相同的实心小铁球紧靠在一起,它们之间的万有引力为F0,若两个半径是小铁球2倍的实心大铁球紧靠在一起,则它们之间的万有引力为( )
A.2F B.4F
C.8F D.16F
解析:小铁球之间的万有引力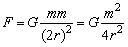
大球半径是小铁球的2倍,其质量分别为:
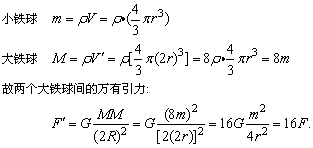
则D成立。
例2、如图所示,半径为R的铅球球心为O,在与球面相切处挖去半径为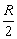 的一个小球,球心在O1,余下月牙形质量为M,在OO1连线外放有一个质量为m的小球,球心为O2,OO2距离为d,试求M,m间的万有引力。 的一个小球,球心在O1,余下月牙形质量为M,在OO1连线外放有一个质量为m的小球,球心为O2,OO2距离为d,试求M,m间的万有引力。

解析:
万有引力定律是宇宙间一条普遍规律,它适用于一切物体间的相互作用。而在公式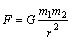 中,说明引力与质量乘积成正比,与距离平方成反比。r不能理解成两物体重心(或质心)间距离,公式是对质点而言的,不能随意应用于一般物体。只有当两物体都是均匀球体或物体间距离非常远,物体的大小与距离比较可忽略不计时,才可应用此公式。若两物体不能看成质点时,应把物体进行分割,使每一小块线度都远小于两者间的距离,然后用叠加的方法求总引力。 中,说明引力与质量乘积成正比,与距离平方成反比。r不能理解成两物体重心(或质心)间距离,公式是对质点而言的,不能随意应用于一般物体。只有当两物体都是均匀球体或物体间距离非常远,物体的大小与距离比较可忽略不计时,才可应用此公式。若两物体不能看成质点时,应把物体进行分割,使每一小块线度都远小于两者间的距离,然后用叠加的方法求总引力。
设想把挖去的那部分填满铅,补上小球的体积,则:
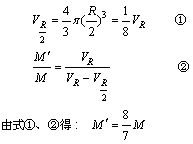
设整个大球对O2球的万有引力为F1,则:
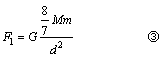 方向水平向左。 方向水平向左。
设补的那个小球对O2球的万有引力为F2,则:
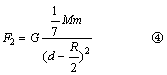 方向水平向左。 方向水平向左。
月牙形对小球O2的万有引力由③、④得:
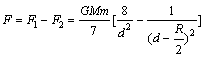 方向水平向左,由O2指向O1。 方向水平向左,由O2指向O1。
(二)万有引力定律在天文学上的应用
1、研究天体运动的基本方法
在天体运动中起决定作用的是万有引力,万有引力定律从动力学角度解决了天体运动问题。
(1)我们近似地把一个天体绕另一个天体的运动看作是匀速圆周运动。向心力就是它们之间的万有引力,即:
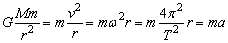
其中M为中心天体的质量,m为做匀速圆周运动的天体的质量,r为轨道半径,即两天体球心间的距离,a为向心加速度。应用时要根据实际情况选用适当的公式进行分析。通常物体之间的万有引力很小,以致察觉不出。但在天体运动中,由于天体的质量很大,万有引力将起决定性的作用。
(2)在不考虑天体自转的情况下,通常认为天体表面上的物体的重力等于它所受的万有引力,即:
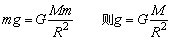
其中M为天体的质量,m为天体表面上物体的质量,R为天体的半径,g为天体的表面的重力加速度。
2、具体应用
(1)求天体质量
(2)求天体平均密度
(3)求天体上物体重力与重力加速度
(4)发现未知天体
(5)人造卫星与宇宙速度(见下一讲)
例3、中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T=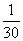 s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67×10-11m3/kg·s2) s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67×10-11m3/kg·s2)
解析:
设想中子星赤道处一小块物质,只有当它受到的万有引力大于或等于它随星体所需的向心力时,中子星才不会瓦解。
设中子星的密度为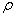 ,质量为M,半径为R,自转角速度为 ,质量为M,半径为R,自转角速度为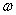 ,位于赤道处的小物块质量为m,则有 ,位于赤道处的小物块质量为m,则有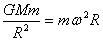 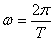 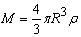
由以上各式得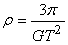 ,代入数据解得: ,代入数据解得: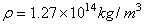 。 。
例4、根据天文学家观测,月球半径为R=1738km,月球表面的重力加速度约为地球表面重力加速度的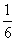 ,月球表面在阳光的照射下温度可达127℃,此时水蒸气分子的平均速度达到v0=2000m/s。试分析月球表面没水的原因。(取地球表面的重力加速度g=9.8m/s2) ,月球表面在阳光的照射下温度可达127℃,此时水蒸气分子的平均速度达到v0=2000m/s。试分析月球表面没水的原因。(取地球表面的重力加速度g=9.8m/s2)
解析:
初看题目的已知条件与所问结果找不到直接联系的东西.但想到若月球表面有水,则月球在转动的同时,月球表面的水团也在随月球转动.由圆周运动知识可知:做圆周运动的物体,当外界提供的向心力F与物体作圆周运动所需要的向心力刚好吻合时,物体做稳定的匀速圆周运动。若外界提供的向心力F小于物体作圆周运动所需要的向心力时,物体将做离心运动而被甩出去.
设在地球表面上任选一部分质量为m的水团,M、R分别为地球的质量和半径。如图1所示,之所以该水团未被甩出去,是因为地球对它的万有引力刚好提供它随地球自转的向心力:
假定月球表面有水,则这些水在127℃时达到的平均速度v0=2000 m/s必须小于月球的第一宇宙速度,否则这些水将不会落回月球表面,导致月球表面无水。取质量为m的某水分子。

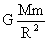 =m =m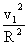 (1) (1)
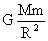 =mg月 (2) =mg月 (2)
g月=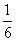 g (3) g (3)
由①②③得:v1=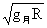 =1700m/s <V 即以2000m/s速度运动的水分子已脱离月球表面,也即月球表面无水。 =1700m/s <V 即以2000m/s速度运动的水分子已脱离月球表面,也即月球表面无水。
例5、“黑洞”是爱因斯坦的广义相对论中预言的一种特殊的天体,它的密度极大,对周围物质(包括光子)有极强的吸引力。根据爱因斯理论,光子是有质量的,光子到达黑洞表面时也将被吸入,最多恰能绕黑洞表面做圆周运动,它自身发出的光子也不能向外射出,人们无法用光学方法观察到它,故称它为“黑洞”,根据天文观测,银河系中心可能有一个黑洞,距该可能黑洞6.0×1012m远的星体正以2.0×106m/s的速度绕它旋转,取G=6.7×10-11N·m2/kg2,试估算该黑洞的质量和半径。(取两位有效数字)
解析:
黑洞作为一个特殊的天体一直受到人们的广泛关注,种种迹象表明它确实存在于人的视野之外由于黑洞的特殊性,一定要抓住其“黑”的原因,即光子也逃不出它的约束,光子绕黑洞作匀周运动时,它的轨道半径就是黑洞的最大可能半径。根据爱因斯坦理论,光自有质量,所以黑洞对光子的引力就等于它做匀速匀周运动的向心力。设黑洞的质量为M,光子的质量为m,光速为c,R为黑洞的可能最大半径。则:
 =m =m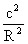 ① ①
银河系中的星体绕黑洞旋转时,也认为做的是匀速匀周运动,其向心力为二者之间的万有引力。设该星体的质量为m′,r为轨道半径。则:
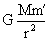 = =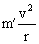 ② ②
由①②式得:R=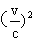 r=3×108m r=3×108m
- 返回 -
|