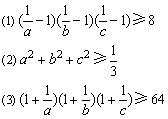|
一、一周知识概述
本周学习第六章不等式的性质和算术平均数与几何平均数两部分内容,前一部分中,主要用于讲述实数运算性质和大小顺序之间的关系,从而掌握比较两个实数大小关系的方法;在此基础上,给出了不等式的性质,一共讲了五个定理和三个推论,并给出了证明.不等式的其他性质都可由它们推导出来.第二部分中课本首先证明了一个重要的不等式a2+b2≥2ab,通过这一公式,得出了两个正数的算术平均数与几何平均数的定理.利用均值不等式求函数的最值问题,这是均值不等式的一个重要应用。最后通过例题,说明此定理在解决数学问题和实际问题中的应用.
二、重难点知识选讲
1、实数的运算性质与大小顺序之间的关系
不等式的等价性:两个实数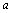 、b比较大小,有大于、等于、小于之别,且有, 、b比较大小,有大于、等于、小于之别,且有,
(1)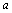 >b >b   -b>0; -b>0;
(2)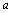 =b =b  -b=0; -b=0;
(3) <b <b  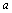 -b<0. -b<0.
等价符号左边不等式反映的是实数的大小顺序,右边不等式反映的则是实数的运算性质,合起来就成为实数的运算性质与大小顺序之间的关系,它是不等式这一章的理论基础,是不等式性质的证明,证明不等式以及解不等式的主要依据.
本周学习的另一重点是用作差法比较两实数的大小.
用作差法比较两实数的大小,其步骤为①作差;②变形;③判断差的正负.在解题中应加强化归意识,把比较大小与实数减法运算联系起来,利用实数的运算性质解决比较大小的问题.
例1、 已知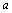 ,b∈R+ ,求证: ,b∈R+ ,求证: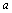 n+bn≥ n+bn≥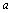 n-1b+ n-1b+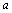 bn-1.(n bn-1.(n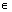 N) N)
[分析与解答]
2、不等式的性质、推论及证明
不等式的五个性质和三个推论是不等式这一章的理论依据。
(1) >b >b b< b< ;(反身性) ;(反身性)
(2)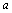 >b,b>c >b,b>c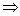 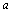 >c;(传递性) >c;(传递性)
(3) >b >b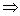 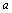 +c>b+c;(两边同加数号不变);推论:移项法则. +c>b+c;(两边同加数号不变);推论:移项法则.
(4)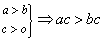 ;(两边同乘正数号不变); ;(两边同乘正数号不变);
(5)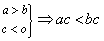 ;(两边同乘负数号改变);推论:去系数法则. ;(两边同乘负数号改变);推论:去系数法则.
(6)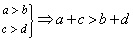 ;(同向相加) ;(同向相加)
(7)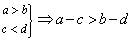 ;(异向相减) ;(异向相减)
(8)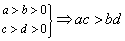 ;(同向相乘) ;(同向相乘)
(9)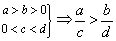 ;(异向相除) ;(异向相除)
(10)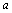 >b >b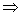 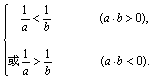 (倒数关系) (倒数关系)
(11)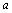 >b>0 >b>0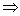 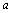 n>b n(n n>b n(n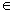 N+);(不等式的幂) N+);(不等式的幂)
(12)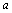 >b>0 >b>0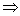 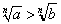 (n (n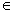 N+);(不等式的方根) N+);(不等式的方根)
例2、已知f(x)=px2-q,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
[分析与解答]
例3、(1)已知30<x<42,16<y<24,求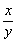 的取值范围. 的取值范围.
(2)已知a,b,x,y都是正数,且 ,求证: ,求证:
[分析与解答]
3、算术平均数与几何平均数
若a、b∈R,那么a2+b2≥2ab(当且仅当a=b时取等号)通常称为重要不等式.两正数a,b的算术平均数 ,几何平均数 ,几何平均数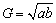 ,平方平均数 ,平方平均数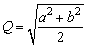 ,调和平均数 ,调和平均数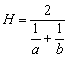 的大小关系为H≤G≤A≤Q(等号当且仅当a=b时取得),这也称作均值不等式.运用重要不等式和均值不等式,可以比较大小,证明不等式,求最值. 的大小关系为H≤G≤A≤Q(等号当且仅当a=b时取得),这也称作均值不等式.运用重要不等式和均值不等式,可以比较大小,证明不等式,求最值.
基本不等式有:
① , ,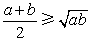 ; ② ; ②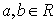 , ,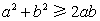 ; ;
③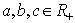 , ,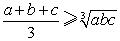 ; ④ ; ④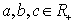 , , ; ;
⑤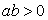 , , ; ;
⑥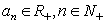 , , . .
例4、已知a,b,c都是正数,且a+b+c=1,求证:
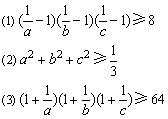
[分析与解答]
利用基本不等式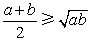 求最值: 求最值:
①当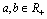 时,不等式 时,不等式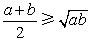 成立; 成立;
②当且仅当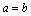 时,不等式 时,不等式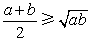 中,“等号”成立; 中,“等号”成立;
③若 为定值,不等式即为 为定值,不等式即为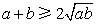 ,当且仅当 ,当且仅当 时, 时,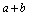 有最小值 有最小值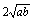 ; ;
④若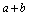 为定值,不等式即为 为定值,不等式即为 ,当且仅当 ,当且仅当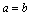 时, 时,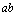 有最大值 有最大值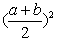 ; ;
注:以上简称“和小积大”;有否最值的关键为是否有定值,且当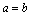 时,能否求出解来. 时,能否求出解来.
例5、已知a,b为正数,且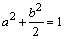 ,求 ,求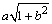 的最大值以及达到最大值时a,b的值. 的最大值以及达到最大值时a,b的值.
[分析与解答]
例6、如图所示,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B孔流出,设箱体的长度为a米,高度为b米,已知流出的水中该杂质的质量分数与a,b的乘积ab成反比,现有制箱材料60平方米,问当a,b各为多少米时,经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)

- 返回 -
|

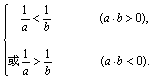 (倒数关系)
(倒数关系)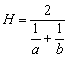 的大小关系为H≤G≤A≤Q(等号当且仅当a=b时取得),这也称作均值不等式.运用重要不等式和均值不等式,可以比较大小,证明不等式,求最值.
的大小关系为H≤G≤A≤Q(等号当且仅当a=b时取得),这也称作均值不等式.运用重要不等式和均值不等式,可以比较大小,证明不等式,求最值.