一、一周知识概述

　　本周学习内容是高二（上）数学第六章第三节，即§6.3不等式的证明，主要介绍不等式证明的基本方法：比较法、综合法、分析法，以及反证法、换元法、函数法、放缩法等。不等式证明的方法较多，通过本周的学习，对知识的掌握要形成系统，能针对具体问题，灵活选用方法．主要是灵活应用不等式的方法证明不等式，通过一题多解培养发散性思维．

二、重难点知识的归纳与剖析

　　本周学习的重点和难点是不等式的证明，特别是掌握好常见的几种证明方法：比较法、综合法、分析法．

比较法：比较法是最基本、最重要的方法，当不等式两边的差能够分解因式或能配成平方和的形式，则选择作差比较法；当不等式两边均为正数且它们的商能与1比较大小，也选择作商比较法．

综合法：从已知或证明过的不等式出发，根据不等式的性质推导出欲证的不等式，综合法的放缩常用到均值不等式．

分析法：不等式的两边联系不够清楚，通过寻找不等式成立的充分条件，逐步将欲证的不等式转化，直到寻找易证或已知成立的结论．

　　用反证法证明不等式时，必须将命题结论的反面的各种情形一一导出矛盾。

　　用换元法要注意换元法的等价性，且要重视置换思想的应用。

　　运用放缩法证明命题时要注意放缩必须适度，放得过大或缩得过小都不能达到证明的目的，放缩时使用的主要方法有：

　　①舍去或加上一些项，如：

　　

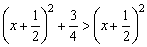
　　②将分子或分母放大（或缩小），如：

　　

三、例题点评

【例1】已知a，b都为正数，且，证明之间．

[解析]

【例2】设a>0,a≠0,0<x<1

　　求证

[解析]

【例3】已知(a＋b)(a2＋b2－1)=2，且a>0，b>0，求证：a＋b≤2．

[解析]

【例4】已知a>0，b>0，c>0，且ab＋bc＋ca=1．

　　求证：(1)a＋b＋c≥;

　　　　 （2）．

[解析]

【例5】已知0<a<1，0<b<1，0<c<1，求证：(1－a)b，(1－b)c，(1－c)a至少有一个小于等于

[解析]

【例6】已知a2＋b2=1，求证：．

[解析]

【例7】设n是正整数，求证

[解析]

【例8】设0<x<1，0<y<1，0<z<1，证明x(1－y)＋y(1－z)＋z(1－x)<1．

[解析]

- 返回 -