（一）本周学习的重点
1、分类计数原理
完成一件事，有n类办法，在第一类办法中有M1种不同的方法，在第二类办法中有M2种不同的办法……在第n类办法中有Mn种不同的方法．那么完成这件事共有N=M1＋M2＋…＋Mn种不同的方法．
本原理也称为加法原理．
2、分步计数原理
完成一件事，需要分成n个步骤，做第一步有M1种不同的方法，做第二步有M2种不同的方法……做第n步有Mn种不同的方法．那么完成这件事共有N=M1×M2×…×Mn种不同的方法．
本原理也称为乘法原理．
在学习这两个原理时应注意以下几点：
（1）分类计数原理和分步计数原理的共同点是把一个原始事件分解成若干个事件来完成，不同点是，分类计数原理与分类有关，分步计数原理与分步有关．
（2）必须搞清楚两个原理的条件和结论．如果完成一件事情有n类办法，这n类办法彼此之间是相互独立的，无论哪一类办法中的哪一种方法都能单独完成这件事情，求完成这件事情的方法种数，就用分类计数原理．
如果完成一件事情需要分成n个步骤，各个步骤都是不可缺少的，需要依次完成所有步骤，才能完成这件事情，而完成每一个步骤有若干种不同的方法，求完成这件事情的方法种数就用分步计数原理．
（3）在解决具体问题时，首先必须弄清楚是“分类”还是“分步”，接着还要搞清楚“分类”或者“分步”的具体标准是什么，与此同时还要注意分类、分步不能重复，不能遗漏．
（4）分类计数原理和分步计数原理是排列、组合问题的最基本的原理，同时也是推导排列数、组合数公式的理论依据，还是求解排列、组合问题的基本思想方法．
3、排列的定义
一般地，从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列．
理解排列定义必须注意的几个问题：
（1）排列的定义中包括两个基本内容，一是“取出元素”，二是“按一定顺序排列”．
（2）从定义知，只有当两个元素完全相同，并且元素排列后的顺序也完全相同时，才是同一个排列，元素完全不同，或元素部分相同或元素完全相同而顺序不同的排列，都不是同一排列，叫不同排列．
（3）在定义中规定m≤n，如果m<n称作选排列，如果m=n，称作全排列．
（4）如何判断一个具体问题是不是排列问题，就看从n个不同元素中取出m个元素后，再安排这m个元素时是有序还是无序，有序就是排列，无序就不是排列．
4、排列数定义
从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号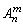
表示．
5、排列数公式
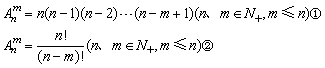
当m=n时，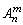
=n·(n－1)·(n－2)·……·2·1
规定0!=1
其中公式①右边从正整数n开始，后一个因数比前一个因数少1，最后一个因数是(n－m＋1)，若n－m个因数相乘，它常用于计算排列数的值，而公式②常用含字母等排列数的变形和证明有关等式．
（二）本周学习的难点
1、在解决具体问题时，何时使用分数计数原理和分步计数原理是难点，特别是对于较复杂的既要用分类计数原理，又要用分步计数原理的问题，我们可以根据题意恰当合理的画出示意图或者列出表格，使问题的实质直观地显现出来，从而便于我们解题．
2、在学习排列时有以下几个难点：
（1）如何判断某个问题是否为排列问题；
（2）不重不漏地写出一些简单的排列；
（3）排列数公式的灵活应用；
（4）会用①特殊元素优先安排；②捆绑法；③插空法；④分情况讨论来解决站排问题．
