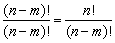1、分类计数原理
分类计数原理：完成一件事，有n类办法，在第1类办法中有m1种不同的方法，在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1＋m2＋…＋mn种不同的方法．
2、分步计数原理：
分步计数原理：完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法……做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×…×mn种不同的方法．
3、两原理的选择
分类计数原理中“完成一件事有n类方法”，是指一件事在一定标准下的分类，标准不同，分类也不同，分类要满足“不重不漏”的原则．完成这件事的各种方法是互相独立、互相排斥的，每一种方法都完成这件事情．
分步计数原理中做一件事的n个步骤，它们之间是相互联系的，每一步都必须取一方法，事情才能完成，单独的每一步都不能独立地完成一件事，下一步选用的方法与上一步方法的选择无关．
两个原理的区别在于一个和分类有关，一个与分步有关．如果完成一件事有n类办法，这n类办法彼此之间是相互独立的，无论哪一类办法中的哪一种方法都能单独完成这件事，求完成这件事的方法种数，就用分类计数原理；如果完成一件事需要分成n个步骤，缺一不可，即需要依次完成所有的步骤，才能完成这件事，而完成每一个步骤各有若干种不同的方法，求完成这件事的方法种数就用分步计数原理．
4、排列定义：
从n个不同的元素中，任取m(m≤n)个元素，按照一定顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列．
在理解这一概念时，应注意以下几个方面
（1）取出m个不同元素（m≤n），无重复元素在同一个排列中．
（2）m个元素按一定顺序排成一列，有顺序说明元素位置不同，则为不同排列．
（3）相同的排列是：元素相同且排列顺序也相同，把它与相同集合区分开，相同集合只需求元素相同而无元素顺序问题．
（4）全排列：当m=n时，称这一排列为n个元素的全排列．
5、排列数
从n个不同的元素中取出m个不同元素的所有排列的个数，叫做n个不同元素中取出m个不同元素的排列数，记作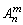
（1）排列数是研究计数问题中的概念，它只管有多少个排列，而重点不在排列是什么上．
（2）符号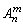
中m，n为正整数，且m≤n，其中
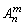是一个整体不能肢解．
6、排列数公式：
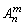=n·(n﹣1)·(n﹣2)·…·(n﹣m﹢1)，规定：0！= 1 .
（1）
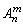表示从n个不同元素中，取出m个元素的排列，当然也表示共得到的排列个数，即它是一个数.
（2）公式右边式子的特点：从一个最大因数n(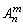
中n)开始，后面每个因素比前面小1，共有m个连续整数，直到n﹣m﹢1.
（3）全排列：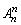
=n(n﹣1)…3×2×1为表示方便，引入阶乘这一计数符号，即n！=n(n﹣1)…3×2×1.便如5！=5×4×3×2×1=120.注意n！=n(n﹣1)！等阶乘间关系．
（4）排列数公式的另一种表示形式：阶乘形式
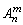=n(n﹣1)…(n﹣m﹢1)·
．