一、一周知识概述

　　本周学习内容是高二上数学第六章的第四节和第五节，本周主要是在复习求解一元一次不等式、一元二次不等式及不等式组的基础上学习一元高次不等式和分式不等式及含绝对值不等式的求解．

二、重难点知识归纳

1、学习的重点

　　本周的学习重点是分式不等式和含绝对值不等式的求解．

（1）分式不等式

　　分式不等式解法的基本思想是将其等价地转化为整式不等式求解，应注意带等号的分式不等式转化时不能忽略分母不为零．

（2）有绝对值的不等式，关键的一步就是要把它等价地转化为不含绝对值的不等式．其主要的转化方法有平方法、分段讨论法、图解法及利用等价命题，即：|x|＞a(a＞0)x＞a或x＜－a，和|x|＜a(a＞0)－a＜x＜a．

定理：|a|－|b|≤|a＋b|≤|a|＋|b|

推论1：|a1＋a2＋a3|≤|a1|＋|a2|＋|a3|

推论2：|a|－|b|≤|a－b|≤|a|＋|b|

　　从定理及推论的公式形式可看出，利用定理和推论可将“和（差）的绝对值”形式放缩成“绝对值的和（差）”形式，为我们在证明不等式的放缩过程中提供理论依据，这也是我们把它们作为本周学习重点的原因．这一作用除了证明一些常用绝对值不等式之外，还为我们的后续学习微积分知识及极限知识打下坚实基础，因此同学们在学习的过程中要注意很好地把握这一点．同学们刚开始学习时，可联系我们以前学过的向量模的知识来理解和记忆．为了加深对定理的理解，可作如下理解：定理实际包含两个绝对值不等式：

|a＋b|≤|a|＋|b|

|a|－|b|≤|a＋b|

　　把它看作一个整体，它实际上由左、中、右三部分组成，右边是绝对值的和，肯定是非负的；中间是和的绝对值，可能因为a，b一正一负要抵消一部分，但由于绝对值，仍是非负的；左边是绝对值的差，当b≠0时，肯定要抵消一部分，而且还可能是负的．这样大、中、小的关系也就容易理解与记忆了．

　　而推论1，只不过是在定理基础上进行项数推广，其推证过程，无非两次运用定理；推论2，虽然形式与定理不同，但实质是等价的，因为定理中a，b是任意实数，所以只要用－b代替b，就可得到．

2、学习的难点

　　利用不等式的性质去分母，利用绝对值的意义去掉绝对值符号，并保持不等式解集的等价性，含绝对值不等式的性质定理的灵活运用是本学点的难点，也是求解两类不等式的关键．

对于高次不等式f(x)>0，其中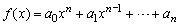.将f(x)分解为若干一次因式的积.

a0(x－x1)(x－x2)…(x－xk)>0.

其中，a0>0，x1<x2<…<xk－1<xk（1≤k≤n），如图所示：

这k个值将数轴分为k＋1个区间（xk，＋∞），（xk－1，xk），（xk－2，xk－1），…，这k＋1个区间从右到左依次编号为第1，2，3，…，k＋1号，那么f(x)>0的解集为第1，3，5，…奇数号区间的并集，概括地说：从右上画起，奇穿偶回（即次数为奇数时就穿过去，次数为偶数时就回来）.

对于分式不等式（或一元高次不等式f(x)＞0）可用根轴法求解，其步骤是：

（1）将f(x)的最高次项的系数化为正数；

（2）将f(x)分解为若干个一次因式的乘积；

（3）将每一个一次因式的根标在数轴上，从右上方依次通过每一点画曲线；

（4）根据曲线呈现出的f(x)值的符号变化规律，写出不等式的解集．

一些含绝对值不等式的证明转化成可利用性质定理或推论来证明的问题，如何进行“拆”、“凑”，只要始终瞄准要证明的不等式的条件和结论，运用分析法的思想，就不难想到“拆”、“凑”的方法，而这一难点的突破，必须从实践中去学习，去摸索．

三、例题点评

例1、已知集合A={x|x3＋2x2－x－2＞0}，B={x|x2＋ax＋b≤0}，且A∪B={x|x＋2＞0}，且 A∩B={x|1＜x≤3}，求实数a，b的值．

[解析]

例2、 解不等式≥3．

[解析]

例3、 解不等式|x2－11x＋21|＞x．

[解析]