|
一、一周知识概述
本周在已经学习了直线和平面，以及空间向量的基础知识，具备了一定的空间想象能力的基础上来研究多面体（棱柱、棱锥）的概念、性质和直观图的画法，通过学习，同学们不仅可以掌握多面体的有关知识，而且还可以巩固前面所学的内容，并且上升到一个理论层次，即同学们通过自行研究，研究多面体的顶点数，面积和棱数之间的关系，得到简单多面体欧拉定理，并尝试将它用来解决化学学科中的有机化学相关问题，同时了解相关的数学家——欧拉的生平，激励我们的学习热情和学习动力；最后研究另一种有代表性的几何体——球，通过学习球的相关概念，了解球作为旋转体的一些特殊性质，并初步接触运用“分割，近似求和，再求极限”的思路推导出球的体积公式和表面积公式，为后续学习微积分奠定心理和思想基础．
二、重、难点知识的归纳与剖析
（一）本周学习与研究中的两个重点
1、棱柱、棱锥的概念以及棱柱、棱锥（包含正棱锥）的性质．
（1）棱柱的概念
有两个面互相平行，其余每相邻两个面的交线互相平行的多面体叫做棱柱．
棱柱是最简单的多面体之一，围成棱柱必须具备两个条件：
①有两个面互相平行；
②其余每相邻两个面的公共边都互相平行，但一定要注意“有两个面互相平行，其余各面都是平行四边形的几何体”不一定是棱柱，如图所示的几何体就不是棱柱．
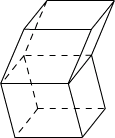
（2）棱柱的性质
根据棱柱的定义，可以得到棱柱有如下性质：
①棱的性质：侧棱都平行，并且都相等；
②面的性质：侧面是平行四边形，两个底面平行且是全等的多边形；
③截面性质：过不相邻的两条侧棱的截面是平行四边形，平行于底面的截面是与底面全等的多边形．
（3）特殊的四棱柱及其它们间的关系
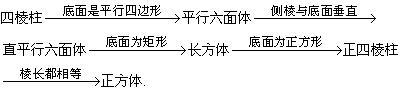
（4）棱锥的概念
有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫棱锥．
棱锥有两个本质特征：
①有一个面是多边形；
②其余的各面是有一个公共顶点的三角形，二者缺一不可，因此有一个面是多边形，其余各面都是三角形的几何体未必是棱锥，棱锥至少有四个面．
如果一个棱锥的底面是正多边形，并且顶点在底面上的射影是底面的中心，这样的棱锥叫正棱锥．
判断一个棱锥是否是正棱锥的条件是：
①底面为正多边形；
②顶点在底面上的射影是底面的中心．
（5）棱锥的性质
①棱锥的平行于底面的截面性质
如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比；
②正棱锥的性质
1°各侧棱相等，各侧面都是全等的等腰三角形；
2°正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形；正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形．
2、球的概念及性质
（1）定义
①球面：半圆以它的直径为旋转轴，旋转所成的曲面．
②球体：球面所围成的几何体．
（2）性质
①任意截面是圆面(经过球心的平面，截得的圆叫大圆，不经过球心的平面截得的圆叫小圆)．
②球心和截面圆心的连线垂直于截面，并且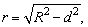 其中R为球半径，r为截面半径，d为球心到截面的距离．
（3）球的任何截面都是圆，过球心的截面是球的大圆，解球的问题，一般是作球的大圆，转化为平面图形来解决．
（4）在球的有关计算中，由球的半径R，截面圆的半径及球心到截面距离O′O构成的直角三角形，也是常用的关键图形．
（二）本周学习与研究中的两个难点
1、欧拉定理的证明与应用
（1）欧拉定理的内容：简单多面体的顶点数V，棱数E及面数F间的关系：V＋F－E=2．
欧拉定理的证明，是将复杂的不易想象的多面体的顶点数、面数、棱数的关系问题转化成我们熟知的易掌握的平面图形的顶点数、面数、棱数的关系问题．这种空间问题平面化的转化思想应予以重视，欧拉公式可看成平面多边形的顶点数V，面数F，棱数E满足的关系式V＋F－E=2的推广形式．
（2）欧拉定理的应用
欧拉定理揭示了多面体的面、顶点和棱之间的内在联系．应用欧拉公式时，先根据已知条件找出三个数中两个和第三个的关系，然后代入欧拉公式求第三个数，最后求出其它两数．
2、球面距离
（1）球面距离的定义
在球面上，两点之间的距离，就是经过这两点的大圆在这两点间的一段劣弧的长度，把这个弧长叫做两点的球面距离．
（2）球面距离的求法
设球面上的两点间的球心角为α弧度，球半径为R，则球面上两点间距离为|α|·R，所以计算球面距离关键是确定球心角．
①当两点在同一经线圆上，可直接计算两点间劣弧长度；
②当两点在同一纬度圆上，先求弦长由余弦定理求球心角，化为弧度，再用l=|α|·r可求得．
③当两点经纬度都不同时，用异面直线上两点间距离公式求弦长，再由余弦定理求球心角．
三、例题点评
例1、正三棱锥S—ABC的底面边长和高都是4，它的内接正三棱柱的三个侧面都是正方形，如图所示，求内接正三棱柱的一个侧面面积．
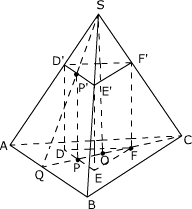
分析：
由于底面与棱锥的底面平行，所以要用到棱锥的平行于底面的截面性质定理．
解答：
法一：设P、P′、Q分别为DE、D′E′，AB的中点，连结SP′，SQ和PP′．
作SO⊥面ABC于O，交面D′E′F′于O′点，得截面SQC．
设棱柱的棱长为x，则：
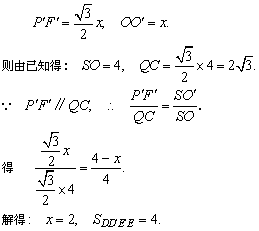
∴ 正三棱柱的一个侧面面积是4．
法二：根据平行于底面的截面与底面多边形的相似比等于截得的棱锥与已知棱锥的高的比得：
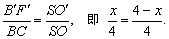
解得：x=2，∴ S侧面=4．
点评：
解内接几何体问题取截面图形非常重要，应使所取的截面图形中能建立起所求与已知之间的联系，便于解决问题．
例2、一个正多面体，各个面的内角和为360°，求它的面数、顶点数和棱数．
分析：本题需从各个面的内角总和入手，再运用欧拉公式进行求解．
解答：设每一个面的边数为m，则：
F·(m－2)·180=3600，
∴ F(m－2)=20．
又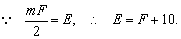
将其代入欧拉公式V＋F－E=2，得V=12．
设过每一个顶点的棱数为n，则 ．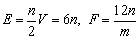
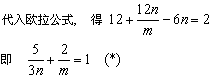
∵ m≥3，∴ n≤5，又n≥3，
∴ n的可取值应当为3，4，5．
当n=3或n=4时，（*）中m无整数解；
当n=5时由（*）得m=3，∴ E=30，∴ F=20．
综上知：E=30，V=12，F=20．
点评：
对于简单多面体V＋F－E是一个不变的常数，其棱数E有三种计算方法：①E=V＋F－2；②E=各面多边形的边长之和的一半；③E=顶点数与共顶点的棱长之积的一半．
例3、设正三棱锥P—ABC的底面边长为a，侧棱长为2a.过A作与PB、PC分别交于D、E的截面．
（1）求截面三角形ADE的周长的最小值；
（2）求截面三角形ADE周长最小时的截面面积．
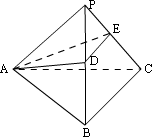
分析：
多面体表面上的两点间的最短距离问题，原则上都要化为平面几何问题加以处理，分析该题图形特点知，正三棱锥各侧面为全等的等腰三角形，它的侧面展开图是一个对称图形．据此寻找已知元素与未知元素的关系，求出待求线段的长度．
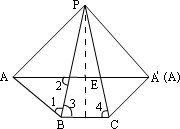
解析：
（1）如图所示，将三棱锥沿PA剪开，展开摊平在一个平面上，显然△ADE的周长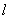 ＝AD＋DE＋EA′≥AA′，则当AD、DE、EA′在一条直线上时，对应的截面△ADE的周长最短，则两点AA′的连线段AA′的长度是△ADE周长的最小值．
由题意，过P作PM⊥BC，则M为BC的中点，而正三棱锥三侧面均为三个全等的等腰三角形，则在图中，正三棱锥的侧面展开图是一个关于PM对称的轴对称图形，则AD＝A′E，且有AA′⊥PM，又PM⊥BC，
∴AA′∥BC ∴∠2＝∠3，∴∠1＝∠2＝∠3＝∠4.
∴AD＝EA′＝AB＝a
∴△ABD∽△P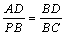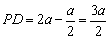BC
∴ ∴
∴ ，又DE∥BC，
∴ ∴ ，
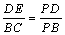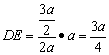故截面△ADE周长最小值为：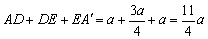
（2）∵△ADE为等腰三角形，又 ，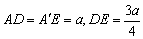
∴DE底边上的高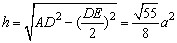
∴ .
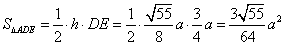点评：
一般地，求最值问题，首先要得到目标函数，然后再借助于函数求最值的方法求出所需的结果．但本题不宜用此法，而应将图形的侧面展开，利用平面上两点之间的线段最短求出这两点间线段的距离即可．
例4、A、B两地都在北纬45°的球面上，它们的经度相差90°，求A、B两点的球面距离．（地球的半径为R）．
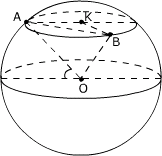
分析：求A、B两地的球面距离，主要求AB两地的球心角大小．
解答：
KA、KB是北纬45°的纬度圈半径， 是A、B两点在这纬度面上所夹劣弧长，则
点评：
球面上两点的球面距离是较难的问题，关键是求出这两点半径所夹的球心角（题中∠AOB），欲求该球心角，必须求出两点弦长．
例5、如图，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱PA⊥平面ABCD，E、F分别是AB、PC的中点．
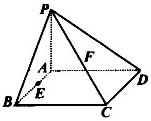
(1)求证：CD⊥PD；
(2)求证：EF∥平面PAD；
(3)当平面PCD与平面ABCD成多大角时，直线EF⊥平面PCD？
分析：
由于底面ABCD是矩形，PA⊥平面ABCD，以A为原点、分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系A—xyz，然后将各问题分别转化为线线平行或垂直来处理．
解：
以A为原点，以AB、AD、AP分别为x轴、y轴、z轴建立空间直角坐标系A—xyz，
设AB=a，AD=b，AP=h，则
A(0，0，0)，B(a，0，0)，D(0，b，0)，P(0，0，h)，C(a，b，0)
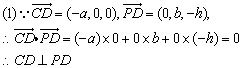
(2)∵E，F分别是AB、PC的中点
(3)由(1)知CD⊥PD，由已知底面为矩形知CD⊥AB，
∴∠PDA为二面角P—CD—A的平面角
∵EF⊥平面PCD，∴EF⊥PD
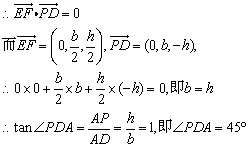
从而当二面角P—CD—A为45°时，EF⊥平面PCD.
点评：用向量处理立体几何问题时注意随时综合运用立体几何知识，可使步骤简捷．
|
