一、一周知识概述

　　本周学习内容是高二（上）数学第七章第四节和第五节，即§7.4简单的线性规则，§7.5研究性课题与实习作业：线性规划的实际应用，共用六个课时，前三个课时主要介绍用二元一次不等式表示区域和简单的线性规划问题．了解线性规划的意义，了解线性约束条件，线性目标函数，可行解，可行域，最优解等基本概念，了解线性规划问题的图解法．后三课时用于研究性学习和实习作业，注意引导学生以所学的数学知识为基础，密切结合生活和生产实际．在学习过程中要充分体现学生的自主活动和合作活动，要教学生学会提出问题和明确探究方向，注意体验数学活动的过程，培养学生的创新精神和应用能力．

二、重难点知识的归纳与剖析

　　本周学习的重点是线性规划问题，线性规划是试验教材所增的重点内容，也是研究性学习的一部分，同时，它也是直线方程知识的应用，是数形结合思想的集中体现，要善于运用它来解决生产生活中的实际问题．

　　本周学习的难点建立数学模型，运用线性规划解题，确定可行域，求最优解．突破的方法是：掌握基本知识和基本方法，抓住规律．在确定可行域时，用带点试验法，或抓住x，y的系数符号，进行判断，在求最优解时，应搞清各直线的倾斜程度，找出最大或最小值时的点．在教学之中，可运用多媒体课件，特别是运用《几何画板》，作出图形，找出最优解，这样既直观又清楚．

　　求线性目标函数的在约束条件下的最值问题的求解步骤是：

　　①画——作图画出约束条件（不等式组）所确定的平面区域和目标函数所表示的平行直线系中的任意一条直线；

　　②移——将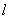平行移动，以确定最优解所对应的点的位置；

　　③求值——解有关的方程组求出最优点的坐标，再代入目标函数，求出目标函数的最值 .

④答——作出答案.

三、例题点评

例1、分别画出下列不等式表示的区域.

（1）x－2y＋2≤0;

（2）x＋2y＋2<0.

[分析、解答、点评]

例2、求不等式|x－2|＋|y－2|≤2所表示的平面区域的面积.

[分析、解答、点评]

例3、解线性规划问题:求z=3x＋y的最大值,使式中的x,y满足约束条件.

[分析、解答、点评]

例4、预算用2000元购买单价为50元的桌子和20元的椅子，希望使桌、椅的总数尽可能多，但椅子不少于桌子，且不多于桌子数的1.5倍，问桌、椅各买多少张才行？

[分析、解答、点评]