|
一、知识概述
本周学习了距离的概念,并重点研究了点到平面的距离,直线到与它平行平面的距离,两个平行平面的距离以及异面直线的距离,其中异面直线的距离是难点.本周所学知识与前面一些相关知识有机结合是立体几何的重点内容.
二、重、难点知识讲解
(一)距离的概念
1、点到面的距离:从平面外一点引一个平面的垂线,这个点和垂足间的距离,叫做这个点到这个平面的距离.
2、直线到它平行平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离.
3、两个平行平面间的距离:两平行平面的公垂线段的长度叫做两平行平面的距离.
4、两条异面直线间的距离是指两条异面直线的公垂线夹在两异面直线间的公垂线段的长度.
(二)各种距离的理解
1、各种距离都是通过垂线或公垂线,按“最短”原则定义的.
①两点距是指连结两点的直线段长;
②点线距离是指该点与直线上任意一点距离的最小值;
③线线距离(包括异面直线的距离)是指分别在这两条直线上的两点距离中最小者;
④点面距则是指该点与平面上任意一点的距离的最小值.
2、“转化”是求上述各种距离最重要的思想方法.在空间距离中,点到面的距离最重要,如线到面的距离和两平行平面的距离都是转化为点到面的距离来表示,异面直线的距离通过作辅助平面也可转化为“线面距”、“面面距”或“点面距”来求.
三、典型例题讲解
1、点到平面距离
点到平面距离的求法一般有两种:(1)直接法:从该点向平面引垂线,确定垂足的位置,求出点与垂足之间的距离,这里常常用到面面垂直的性质定理;(2)向量法:计算点向平面所引斜线段对应的向量在平面法向量上的投影,或计算点与垂足连线段对应向量的模.
例1、如图,已知 ABCD 是边长为 4 的正方形,E、F分别是AB、AD的中点,GC垂直于平面ABCD,且GC=2,求点B到平面EFG的距离 .
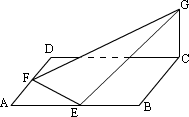
分析:
从图中易知,直接从 B 点向平面作射影,不知射影位置如何,无法求 . 但通过连结 BD,由 EF∥BD,知 BD∥平面 GEF,于是考虑通过线面距离来转移求解 .
解析:
如图连结AC、BD,设 AC∩BD=O, AC∩EF=H,由 E、F为中点知 EF∥BD,
∴ BD∥平面 EFG,则 O 点到平面 EFG 的距离就等于 B 点到平面 EFG 的距离.
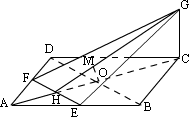
∵ GC⊥平面 ABCD,∴ GC⊥BD.
又∵ ABCD 为正方形,∴ AC⊥BD.
∴ BD⊥平面 GCH,即 EF⊥平面 ECH.
过O作 OM⊥GH 于 M,则有 OM⊥平面 GEF,即 OM 长为所求距离.
由 Rt△OMH∽Rt△GCH,知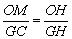 . .
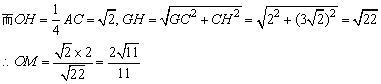
故点 B 到平面 EFG 的距离为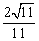 . .
2、直线到与它平行平面的距离
由于直线上任一点到与它平行的平面的距离都相等,所以线面距离一般是转化为点到平面的距离求解.
例2、如图,四边形ABCD是菱形,P是平面ABCD外一点,PA⊥平面ABCD,且PA=4,AB=4,E是PA的中点,∠ABC=60°.

(1)求证:平面BED⊥平面PAC;
(2)求PC与平面BED间的距离.
解:(1)证明:∵PA⊥ABCD,∴BD⊥PA.
又ABCD是菱形,∴BD⊥AC.∴BD⊥面PAC,
∴面BED⊥面PAC.
(2)解:连结EO则EO∥PC,
∴PC∥面BED,作EF⊥PC于F,则EF⊥EO,EF⊥面BDE,
∴EF的长为PC到平面BED的距离,
PE=2,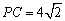 ,∴ ,∴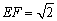 . .
即PC与平面BED间的距离为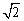 . .
评析:
求线面距离可转化为点面距离,反之求点面距离也可转化为线面距离,再转化为点面距离,因此点到面的距离是重中之重.
3、两个平行平面的距离
求解两个平行平面的距离时,在一个平面内任取一点,作它到另一平面的垂线段,垂线段的长就是所求.实质上也是点到平面的距离,因此,点面距离的求解方法,对求解面到面的距离仍然适用.
例3、在直二面角C—BB1-A中,四边形AA1B1B与四边形CC1B1B为矩形,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D、F、G分别为CC1、C1B1、C1A1的中点.
(1)求证:B1D⊥平面ABD;
(2)求证:平面EGF∥平面ABD.
(3)求平面EGF与平面ABD的距离.
分析:
本题建立坐标系解题较为方便.证明两面平行时,利用垂直于同一条直线的两个平面互相平行.
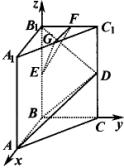
解:
(1)如图,由条件知,BA、BC、BB1两两互相垂直,以B为坐标原点,BA、BC、BB1所在直线分别为x轴、y轴、z轴建立直角坐标系.
由条件知,B(0,0,0)、D(0,2,2)、B1(0,0,4),
设BA=a,则A(a,0,0).
所以,
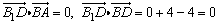
所以,B1D⊥BA,B1D⊥BD,因此B1D⊥平面ABD.
(2)由E、F、G的定义知,E(0,0,3), ,F(0,1,4). ,F(0,1,4).
所以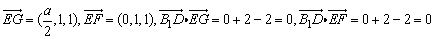 . .
所以B1D⊥EG,B1D⊥EF,B1D⊥平面EFG,结合(1)可知,面EGF∥面ABD.
(3)由(1)、(2)知,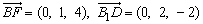 是平面ABD的法向量. 是平面ABD的法向量.
所以 上的射影长 上的射影长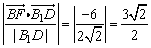 . .
所以点F到平面ABD的距离为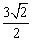 . .
由(2)知,面EGF与面ABD的距离=点F到面ABD的距离=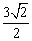 . .
4、异面直线的距离
两条异面直线间的距离,要特别注意定义中的“都垂直且相交”的理解,两条异面直线距离是分别连结两条异面直线上两点的线段中最短的一条.
异面直线距离是本节课的难点,求异面直线的距离,通常有如下思路:
(1)直接作出或找出两异面直线的公垂线段并求其长. 在作的时候,要充分利用线面垂直 .
(2)作出或找到过异面直线中的一条与另一条平行的平面,转化为求线面距离.
例4、如图,已知空间四边形 ABCD 各边及对角线长都是a,求异面直线AB,CD的距离.

分析:
立体几何解题中,我们要充分利用等边,等腰等特殊图形的中线即为高线进行线面,线线垂直关系的讨论.
解:
取 CD 的中点为 E ,连 AE,BE,
∵ AC=AD,∴ AE⊥CD ,同理, BE⊥CD.
∴ CD⊥平面 AEB ,且 AE=BE ,又取 AB 中点为 F ,
连 EF ,则有 EF⊥AB,EF⊥CD,
即 EF 为 AB、CD 的公垂线段.
而 EF=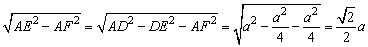 . .
故异面直线 AB、CD 间的距离为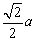 . .
|