|
一、一周知识概述
本周主要是学习了二面角、两个平面垂直的判定与性质.要求理解二面角的定义,会作出二面角的平面角,并能通过解三角形等方法求其大小,会根据定义和判定定理判定两个平面垂直,
二、重难点知识讲解
1、二面角和二面角的平面角
从一条直线出发的两个半平面所组成的图形叫做二面角。
以二面角的棱上任意一点为端点,在两个面分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
二面角的平面角,则是用来刻划二面角大小的一个概念。它和两条异面直线所成的角以及直线和平面所成的角一样,都化归为平面内两条相交直线所成的角来表示。但必须注意二面角的平面角所在平面应垂直于二面角的棱,二面角的平面角的两条边分别在二面角的两个面内。而二面角的平面角的大小是由二面角的两个面的相互位置所确定的,与二面角的平面角的顶点在棱a上的位置无关.
作二面角的平面角有三种作法:
(1)定义法:在棱上选取一点,过该点分别在两个平面内作棱的垂线,这两条射线所成的角即是.
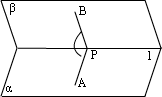
(2)垂面法:在二面角的棱上任选一点,过该点作棱的垂面,垂面与两个半平面相交,则交线所成的角为二面角的平面角.
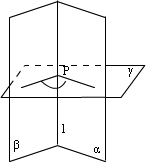
(3)垂线法:在二面角α—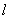 —β的一个平面α内任取一点A(不在棱 —β的一个平面α内任取一点A(不在棱 上),过A作AB⊥β于B,过A作AO⊥ 上),过A作AB⊥β于B,过A作AO⊥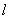 于O(或过B作BO⊥ 于O(或过B作BO⊥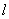 于O),连接BO(或AO),则∠AOB为二面角的平面角. 于O),连接BO(或AO),则∠AOB为二面角的平面角.
2、求二面角的大小的步骤:
(1)通过求二面角的平面角求二面角.
二面角的大小,可以用它的平面角来度量,所以我们求二面角关键是作(或找)出它的平面角,再求出它的平面角的大小,二面角的平面角有以下几种作法.
①定义法:根据定义作垂直于棱的平面得平面角.
②垂线法:过棱上一点分别在两个面内作棱的垂线得平面角.
③三垂线定理或逆定理法:
过二面角一个平面内的一点P,作另一个面的垂线(常利用面面垂直的性质定理),记垂足为H1,再过H1(或P)作棱的垂线,记垂足为H2,连PH2、H1H2,由三垂线定理及其逆定理可知∠PH2H1即为所求二面角的平面角.
(2)射影法
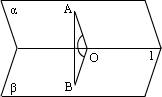
设θ为所求二面角的大小,S为二面角的一个面内的平面图形的面积,Sˊ为该平面图形在另一个面内的射影所组成的平面图形的面积,则cosθ=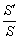 .利用此射影面积公式,求二面角. .利用此射影面积公式,求二面角.
在求二面角时,垂线法应用最多,要重点注意。
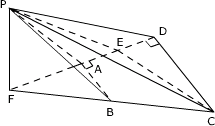
例1、如图所示,四棱锥P—ABCD底面为一直角梯形,BA⊥AD,CD⊥AD,且AB=2,CD=4,侧面PAD⊥底面ABCD,侧面PBC为边长等于10的正三角形.
(1)求PC与底面所成角正弦值的大小;
(2)求侧面PAD与侧面PBC所成的二面角的余弦值.
[解析]
3、两个平面互相垂直的定义及画法
(1)如果两个相交平面所成的二面角为直二面角,那么这两个平面互相垂直,平面α和平面β垂直,记作α⊥β.
(2)画两个互相垂直的平面,把直立平面的竖边画成和水平面的横边垂直.
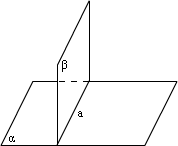
4、两个平面垂直的判定定理
(1)两个平面垂直的判定定理:如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直.
用符号表示为: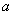 ⊥β, ⊥β,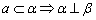 . .
(2)用来判定两个平面垂直的方法有两种:
①根据定义,两个平面相交,它们所形成的二面角是直二面角,通常先作出二面角的平面角,再证明二面角的平面角是直角;②根据判定定理,证明一个平面过另一个平面的一条垂线,即把面面垂直问题化归为线面垂直问题.这个定理可简记为“线面垂直,面面垂直”.
例2、 如图,在空间四边形 ABCD 中, AB=BC,CD=DA,E,F,G 分别为 CD,DA 和 AC 的中点,求证:平面 BEF⊥平面 BGD.
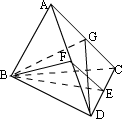
[解析]
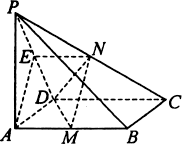
例3、如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.
(1)求平面PCD与平面ABCD所成的二面角的大小;
(2)求证:平面MND⊥平面PCD.
[解析]
5、两个平面垂直的性质定理
(1)性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
(2)常见的结论还有:
①如果两个平面互相垂直,那么经过第一个平面内的一点,垂直于第二个平面的直线,在第一个平面内.
②如果两个平面都垂直于第三个平面,那么它们的交线必垂直于这个平面.
例4、判断下列命题的真假
(1)两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面;
(2)两个平面垂直,分别在这两个平面内且互相垂直的两直线,一定分别与另一平面垂直;
(3)两平面垂直,分别在这两个平面内的两直线互相垂直.
[解析]
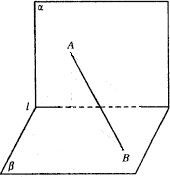
例5、已知AB是夹在直二面角α-l-β内的一条线段,如图A∈α,B∈β,AB与α、β分别成45°和30°的角,AB=a,求AB在l上的射影长及AB与l所成角的大小.
[解析]
|