|
一、一周知识概述
本周学习第九章第七节:棱柱.主要内容是棱柱的概念,棱柱的性质及斜二测画法.要求了解棱柱的概念,并能区别棱柱、直棱柱、正棱柱等概念,特别是四棱柱中的几个概念,只有区别,才能抓住它们的性质,在解题中才能合理地应用。注意准确理解直棱柱、正棱柱的的概念,从底面,侧面,棱和截面四个方面掌握棱柱几何体的性质,应用性质研究其中的线面关系。简单多面体的画法,虽然不会直接考查,但是它是解决立体几何的基本功,应予以高度重视。
二、本周重难点知识
1、棱柱的概念
有两个面互相平行,其余每相邻的两个面的交线互相平行的多面体叫棱柱.
两个互相平行的面叫棱柱的底面,简称底;其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两个底面所在平面的公垂线段叫做棱柱的高.
侧棱不垂直于底面的棱柱叫斜棱柱;侧棱垂直于底面的棱柱叫直棱柱,底面是正多边形的直棱柱叫做正棱柱.
棱柱按底面分为三棱柱,四棱柱,……
2、棱柱的性质
一般棱柱:所有的侧棱都相等,各个侧面都是平行四边形;两底面与平行于底面的截面是对应边互相平行的全等多边形;过不相邻的两侧棱的截面为平行四边形。
正棱柱:侧棱与底面垂直,侧面为全等的矩形;两底面与平行于底的截面为全等的正多边形;直棱柱的侧面展开图为矩形。
3、棱柱间的关系
棱柱
四棱柱 平行六面体 平行六面体 直平行六面体 直平行六面体
 长方体 长方体 正四棱柱 正四棱柱 正方体 正方体
4、长方体的相关结论
设长方体的三条棱长分别为a、b、c,则
(1)对角线长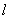 = = ; ;
(2)表面积S=2(ab+bc+ac);
(3)体积V=abc;
(4)若对角线与过同一顶点的三条棱所成的角分别为α、β、γ,
则cos2α+cos2β+cos2γ=1;
(5)若对角线与过同一顶点的三个面所成的角分别为α、β、γ,
则cos2α+cos2β+cos2γ=2.
5、棱柱的侧面积
(1)如果直棱柱的底面周长是c,高是h,那么它的侧面积是S直棱柱侧=ch;
(2)斜棱柱的侧面积等于它的直截面(垂直于侧棱并与每条侧棱都相交的截面)的周长与侧棱长的乘积.
6、棱柱的体积
V=S·h,其中S是底面积,h是高;V长方体=abc,其中a、b、c是长方体的长、宽、高;V正方体=a3,其中a是正方体的棱长.
7、直观图的画法
(1)水平放置的平面图形直观图的画法——斜二测画法;
(2)直棱柱的直观图的画法(与平面图形的斜二侧画法相比,只是多画一个与x轴、y轴都垂直的z轴,并且平行于z轴的线段的平行性和长度都不变).
三、例题选讲
例1、下列命题中,不正确的是( )
A.棱长都相等的长方体是正方体
B.有两个相邻侧面为矩形的棱柱为直棱柱
C.有两个侧面与底面垂直的棱柱为直棱柱
D.底面为平行四边形的四棱柱叫平行六面体
分析:
由平行六面体、正方体的定义知A、D正确,对于B,相邻两侧面垂直于底面,侧棱垂直于底面,该棱柱为直棱柱,因而B正确,对于C若两侧面平行且垂直于底面,则不一定是直棱柱.
答案:C
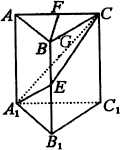
例2、如图所示,在正三棱柱ABC—A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
(1)求证:BE=EB1;
(2)若AA1=A1B1,求平面A1EC与平面A1B1C1所成二面角(锐角)的度数.
分析:
证明BE=EB1,关键要利用正三棱柱性质解题;求二面角的大小,要作出二面角的平面角,因而首先确定二面角的棱.
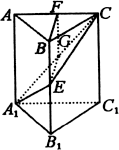
(1)证明:在截面A1EC内,过E作EG⊥A1C,G是垂足,
∵平面A1EC⊥平面AC1,∴EG⊥侧面AC1,
取AC的中点F,连结BF、FG,由AB=BC,得BF⊥AC,
∵平面ABC⊥侧面AC1,∴ BF⊥侧面AC1.
∴ BF∥EG,BF、EG确定一个平面,交侧面AC1于FG.
∵ BE∥侧面AC1,∴BE∥FG,
∴四边形BEGF是平行四边形,∴BE=FG.
∴ BE∥AA1,∴FG∥AA1,△AA1C∽△FGC.
∵ AF=FC,∴FG=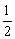 AA1= AA1=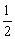 BB1, BB1,
即BE=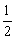 BB1,故BE=EB1. BB1,故BE=EB1.
(2)解答:如图,分别延长CE,C1B1交于点D,连A1D.
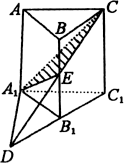
∵ EB1∥CC1,EB1= BB1= BB1=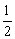 CC1, CC1,
∴ DB1=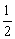 DC1=B1C1=A1B1. DC1=B1C1=A1B1.
∵∠B1A1C1=∠B1C1A1=60°,
∠DA1B1=∠A1DB1= (180°-∠DB1A1)=30°. (180°-∠DB1A1)=30°.
∴∠DA1C1=∠DA1B1+∠B1A1C1=90°,即DA1⊥A1C1.
∵ CC1⊥平面A1C1B1,即A1C1是A1C在平面A1C1B1上的射影,
由三垂线定理得DA1⊥A1C.
∴∠CA1C1是所求二面角的平面角.
∴CC1=AA1=A1B1=A1C1,∠A1C1C=90°.
∴∠CA1C1=45°.即所求二面角为45°.
点评:
本题可不作二面角的平面角,利用射影面积定理求角,设△ABC的边长为a,截面A1EC和底面所求二面角为θ,可求得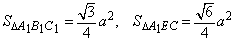 ,由cosθ= ,由cosθ= ,求得θ=45°. ,求得θ=45°.
例3、如图, 正四棱柱A1B1C1D1—ABCD的底面边长为a ,高为h, 过点B的直线EF在正四棱柱下底面所在的平面内,且EF⊥BD,过EF作与底面成30°角的平面,该平面与正四棱柱的截面为BGHK.求四边形BGHK的周长和面积.
分析:
利用正棱柱定义找出二面角的平面角∠HBD,通过解直角三角形求得边长。
解:
如图,延长DC交EF于F,延长DA交EF于E,连结HF交CC1于G,连结HE交AA1于K,连结GB、KB,连结BH、GK,DB⊥EF, HB⊥EF, ∠HBD=30°,
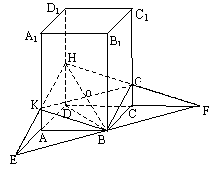
在Rt△HDB中, BD=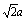 ,HD= ,HD=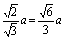 ,HB=2HD= ,HB=2HD=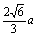 ,KG= ,KG=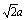 , ,
在四边形BGHK中,HG//KB,HK//GB,HB与KG互相垂直平分.
∴ 四边形BGHK为菱形, KB=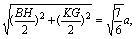
∴四边形BGHK的周长=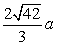 , ,
面积SBGHK =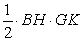 = =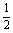 · ·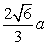 · ·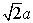 = = . .
点评:解多面体有关问题,必须借助线、面间各种位置关系的判定和性质.
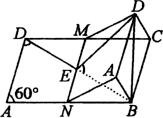
例4、如图,平行四边形ABCD中,∠A=60°,AD=a,AB= 2a,M,N分别是CD,AB的中点,以MN为二面角的棱将面ADMN折起;
(1)当二面角A—MN—B为60°时,求三棱柱ABN—DCM的体积;
(2)当二面角A—MN—B为多大时,此三棱柱的体积有最大值?并求出最大值.
分析:
折叠成的三棱柱是斜三棱柱,求其底面积和高较难,则可利用直截面面积与侧棱的乘积求得.
解答:(1)如图所示,折起前连结BD交MN于E,
由余弦定理得
BD2=AD2+AB2-2AD·AB·cos60°=a2+(2a)2-2a·2a·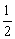 =3a2. =3a2.
∵ AB2=AD2+BD2,
∴∠ADB=90°,即AD⊥BD.
又∵ MN∥DA,∴MN⊥BD.
折起后,DE、MN都在同一平面ADMN内,
∴ DE⊥MN,同理BE⊥MN,
∴∠DEB是二面角A—MN—B的平面角.
即∠DEB=60°,且DEB是三棱柱的直截面.
∵ DE=BE=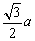 ,△DEB是等边三角形, ,△DEB是等边三角形,
∴ S△DEB=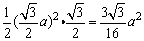 , ,
∴ V柱=AD·S△DEB=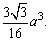
(2)设∠DEB=α,则S△DEB=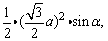
V柱=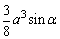 , ,
当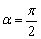 时,sinα有最大值,∴V柱有最大值 时,sinα有最大值,∴V柱有最大值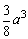 . .
故二面角A-MN-B的平面角是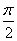 时,棱柱的体积的最大值为 时,棱柱的体积的最大值为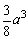 。 。
点评:
求斜棱柱的体积.侧面积一般都用棱柱的直截面.在折叠问题的处理中,应特别注意折叠前的点、线、面及数量关系和折叠后的变化情况,一般来说,在同一平面时折叠前后的关系不变,不在同一平面时,折叠后可能发生变化,应引起注意.
|